Sampling of Correlated Bandlimited Continuous Signals by Joint Time-vertex Graph Fourier Transform

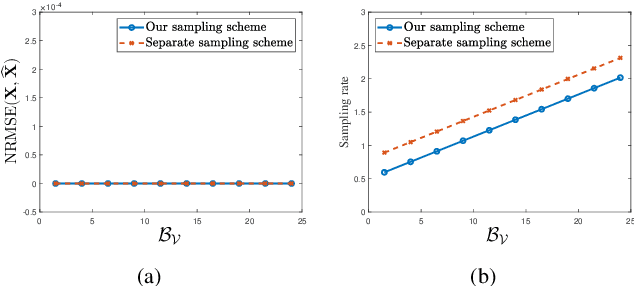
When sampling multiple signals, the correlation between the signals can be exploited to reduce the overall number of samples. In this paper, we study the sampling theory of multiple correlated signals, using correlation to sample them at the lowest sampling rate. Based on the correlation between signal sources, we model multiple continuous-time signals as continuous time-vertex graph signals. The graph signals are projected onto orthogonal bases to remove spatial correlation and reduce dimensions by graph Fourier transform. When the bandwidths of the original signals and the reduced dimension signals are given, we prove the minimum sampling rate required for recovery of the original signals, and propose a feasible sampling scheme.