Generalized Graphon Process: Convergence of Graph Frequencies in Stretched Cut Distance
Paper and Code
Sep 11, 2023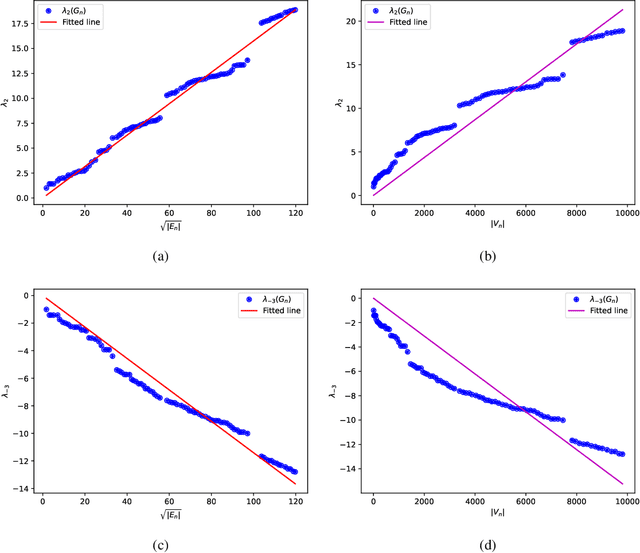
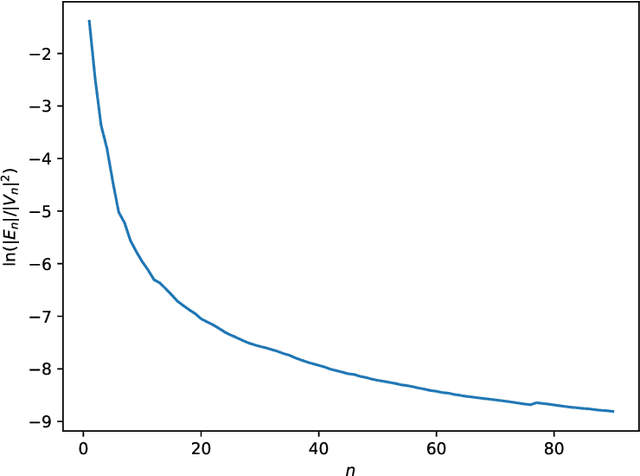
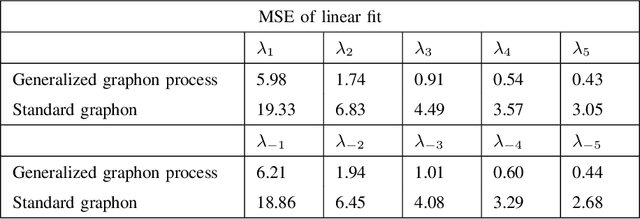
Graphons have traditionally served as limit objects for dense graph sequences, with the cut distance serving as the metric for convergence. However, sparse graph sequences converge to the trivial graphon under the conventional definition of cut distance, which make this framework inadequate for many practical applications. In this paper, we utilize the concepts of generalized graphons and stretched cut distance to describe the convergence of sparse graph sequences. Specifically, we consider a random graph process generated from a generalized graphon. This random graph process converges to the generalized graphon in stretched cut distance. We use this random graph process to model the growing sparse graph, and prove the convergence of the adjacency matrices' eigenvalues. We supplement our findings with experimental validation. Our results indicate the possibility of transfer learning between sparse graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge