Conformal Prediction for Multi-Source Detection on a Network

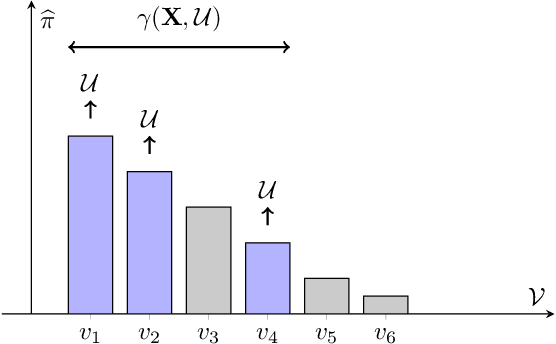
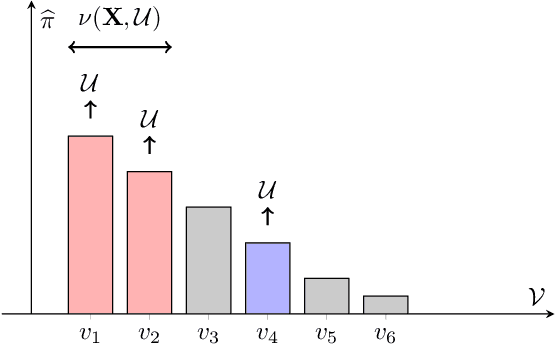
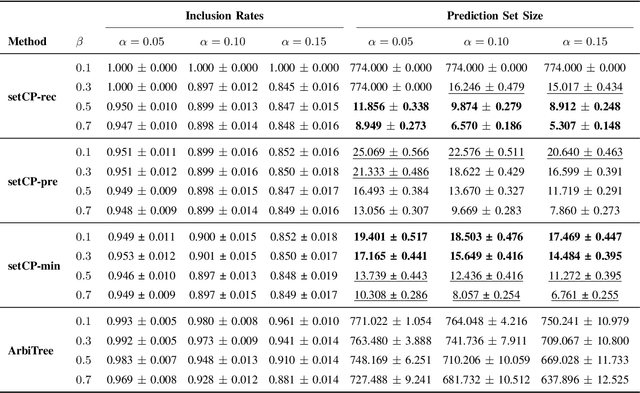
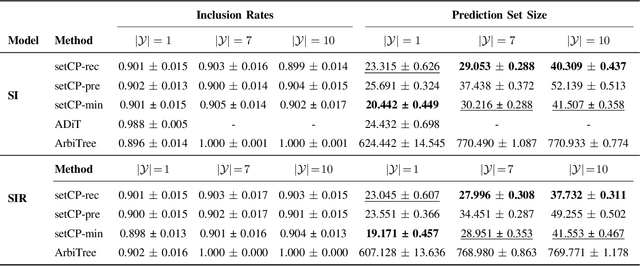
Detecting the origin of information or infection spread in networks is a fundamental challenge with applications in misinformation tracking, epidemiology, and beyond. We study the multi-source detection problem: given snapshot observations of node infection status on a graph, estimate the set of source nodes that initiated the propagation. Existing methods either lack statistical guarantees or are limited to specific diffusion models and assumptions. We propose a novel conformal prediction framework that provides statistically valid recall guarantees for source set detection, independent of the underlying diffusion process or data distribution. Our approach introduces principled score functions to quantify the alignment between predicted probabilities and true sources, and leverages a calibration set to construct prediction sets with user-specified recall and coverage levels. The method is applicable to both single- and multi-source scenarios, supports general network diffusion dynamics, and is computationally efficient for large graphs. Empirical results demonstrate that our method achieves rigorous coverage with competitive accuracy, outperforming existing baselines in both reliability and scalability.The code is available online.

Frequency Convergence of Complexon Shift Operators (Extended Version)

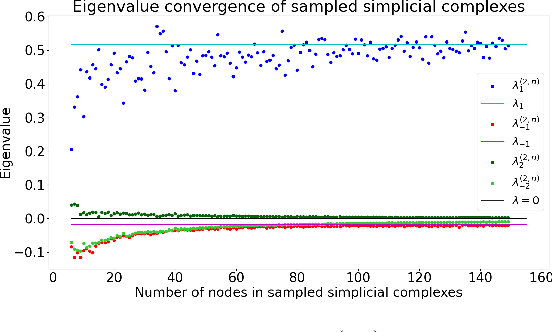
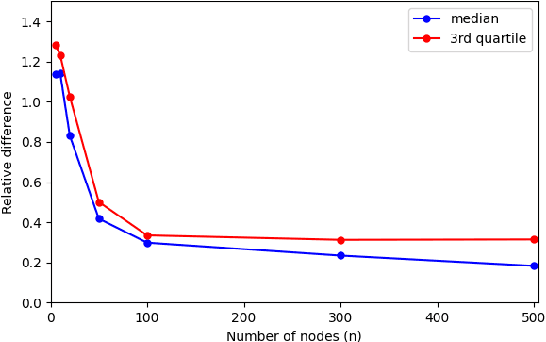
Topological Signal Processing (TSP) utilizes simplicial complexes to model structures with higher order than vertices and edges. In this paper, we study the transferability of TSP via a generalized higher-order version of graphon, known as complexon. We recall the notion of a complexon as the limit of a simplicial complex sequence. Inspired by the integral operator form of graphon shift operators, we construct a marginal complexon and complexon shift operator (CSO) according to components of all possible dimensions from the complexon. We investigate the CSO's eigenvalues and eigenvectors, and relate them to a new family of weighted adjacency matrices. We prove that when a simplicial complex sequence converges to a complexon, the eigenvalues of the corresponding CSOs converge to that of the limit complexon. This conclusion is further verified by a numerical experiment. These results hint at learning transferability on large simplicial complexes or simplicial complex sequences, which generalize the graphon signal processing framework.