Sparse graph sequences, generalized graphons and signal processing

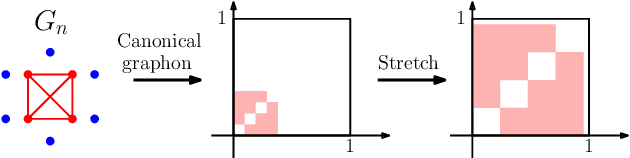
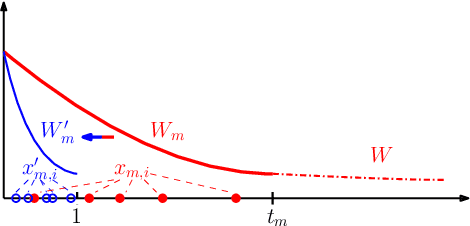
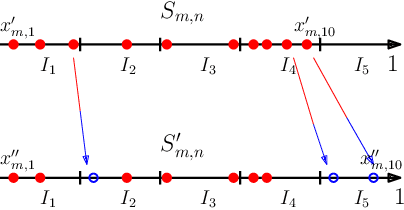
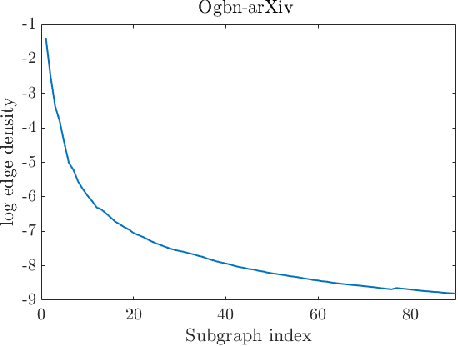
Graphons are limit objects of sequences of graphs, used to analyze the behavior of large graphs. Recently, graphon signal processing has been developed to study large graphs from the signal processing perspective. However, it has the shortcoming that any sparse sequence of graphs always converges to the zero graphon, and the resulting signal processing theory is trivial. In this paper, we propose a signal processing framework based on the generalized graphon theory. The main ingredient is to use the stretched cut distance to compare these graphons. We focus on sampling graph sequences from generalized graphons, and discuss convergence results of associated operators, spectrum as well as signals. Though the paper is theoretical, we also discuss what the theory implies for real large networks.