Aylin Tastan
Fast and Robust Sparsity-Aware Block Diagonal Representation
Dec 02, 2023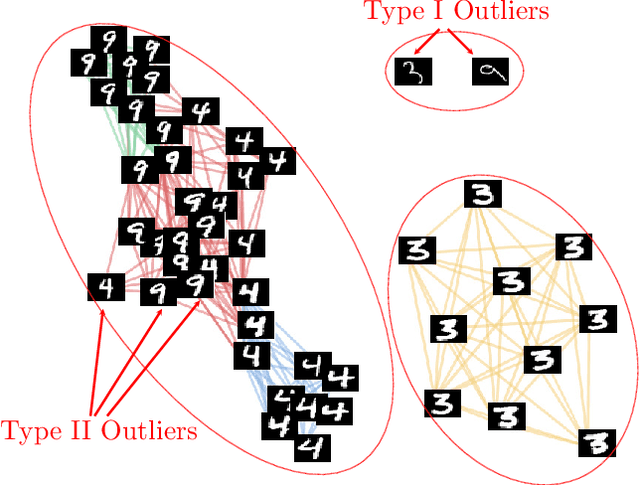
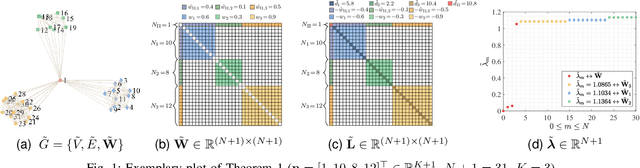
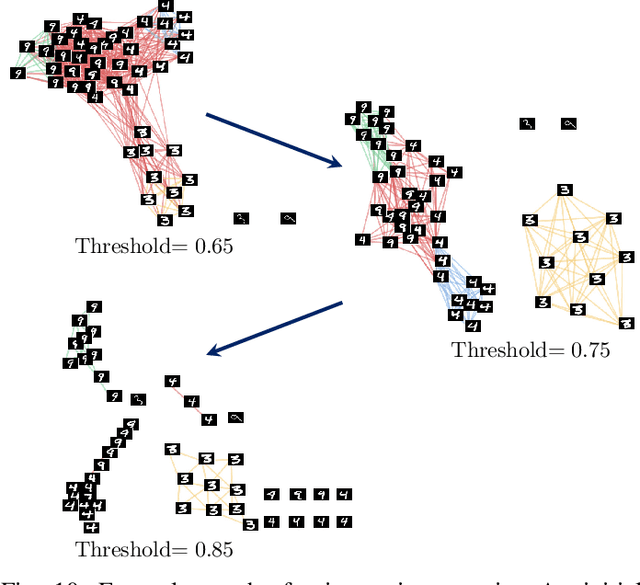
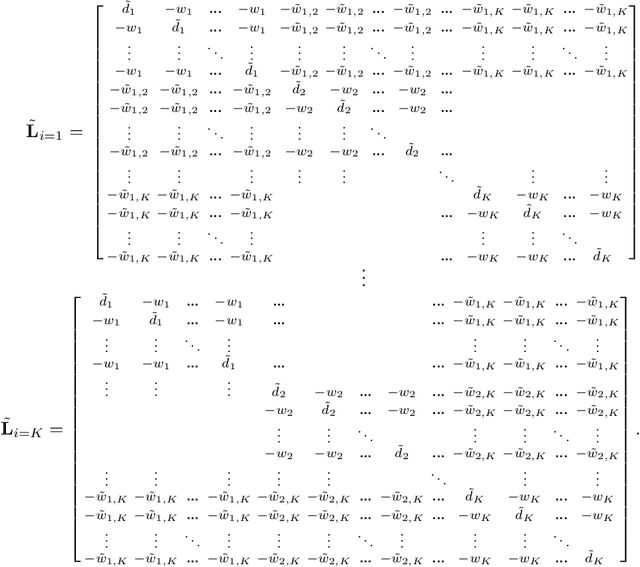
Abstract:The block diagonal structure of an affinity matrix is a commonly desired property in cluster analysis because it represents clusters of feature vectors by non-zero coefficients that are concentrated in blocks. However, recovering a block diagonal affinity matrix is challenging in real-world applications, in which the data may be subject to outliers and heavy-tailed noise that obscure the hidden cluster structure. To address this issue, we first analyze the effect of different fundamental outlier types in graph-based cluster analysis. A key idea that simplifies the analysis is to introduce a vector that represents a block diagonal matrix as a piece-wise linear function of the similarity coefficients that form the affinity matrix. We reformulate the problem as a robust piece-wise linear fitting problem and propose a Fast and Robust Sparsity-Aware Block Diagonal Representation (FRS-BDR) method, which jointly estimates cluster memberships and the number of blocks. Comprehensive experiments on a variety of real-world applications demonstrate the effectiveness of FRS-BDR in terms of clustering accuracy, robustness against corrupted features, computation time and cluster enumeration performance.
Robust Regularized Locality Preserving Indexing for Fiedler Vector Estimation
Jul 26, 2021



Abstract:The Fiedler vector of a connected graph is the eigenvector associated with the algebraic connectivity of the graph Laplacian and it provides substantial information to learn the latent structure of a graph. In real-world applications, however, the data may be subject to heavy-tailed noise and outliers which results in deteriorations in the structure of the Fiedler vector estimate. We design a Robust Regularized Locality Preserving Indexing (RRLPI) method for Fiedler vector estimation that aims to approximate the nonlinear manifold structure of the Laplace Beltrami operator while minimizing the negative impact of outliers. First, an analysis of the effects of two fundamental outlier types on the eigen-decomposition for block affinity matrices which are essential in cluster analysis is conducted. Then, an error model is formulated and a robust Fiedler vector estimation algorithm is developed. An unsupervised penalty parameter selection algorithm is proposed that leverages the geometric structure of the projection space to perform robust regularized Fiedler estimation. The performance of RRLPI is benchmarked against existing competitors in terms of detection probability, partitioning quality, image segmentation capability, robustness and computation time using a large variety of synthetic and real data experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge