Shrinkage priors for Bayesian Substitute Confounders

Multi-cause observational studies contain information about unmeasured confounding through the dependence structure among causes. However, literal imputation of the unobserved confounder is often more complex than learning a lower-dimensional substitute score that preserves the shared assignment variation needed for stable causal adjustment. The deconfounder (Wang and Blei, 2019) and related substitute confounder methods exploit this idea, but flexible assignment models can fit the joint distribution of the causes while producing scores that over-encode the treatment vector, collapse overlap, or capture single-cause variation. We develop a Bayesian factor assignment framework for learning sparse substitute confounders that retain coarse multi-cause dependence with shrinkage priors. The theory is stated at the level of posterior concentration, factor score contraction, and overlap-preserving assignment geometry and therefore does not rely on a particular shrinkage prior. Under these conditions, the proposed regression-adjusted estimators are consistent for mean potential outcomes when the corresponding latent variable identification assumptions hold. Shrinkage priors provide a natural tool for latent structural learning: they favour low-dimensional factors supported by multiple causes, discourage effectively single-cause factors, and induce an ordering of the latent factors through progressive shrinkage. Synthetic experiments illustrate the roles of signal strength, outcome validity, and geometry-aware regularization. In an Alzheimer's Disease Neuroimaging Initiative (ADNI) baseline analysis, sparse substitute scores recover much of the adjustment obtained by directly conditioning on invasive cerebrospinal-fluid biomarkers, while collapse diagnostics identify when fitted factors reduce to individual observed measurements.

Kernel-based estimators for functional causal effects

We propose causal effect estimators based on empirical Fr\'{e}chet means and operator-valued kernels, tailored to functional data spaces. These methods address the challenges of high-dimensionality, sequential ordering, and model complexity while preserving robustness to treatment misspecification. Using structural assumptions, we obtain compact representations of potential outcomes, enabling scalable estimation of causal effects over time and across covariates. We provide both theoretical, regarding the consistency of functional causal effects, as well as empirical comparison of a range of proposed causal effect estimators. Applications to binary treatment settings with functional outcomes illustrate the framework's utility in biomedical monitoring, where outcomes exhibit complex temporal dynamics. Our estimators accommodate scenarios with registered covariates and outcomes, aligning them to the Fr\'{e}chet means, as well as cases requiring higher-order representations to capture intricate covariate-outcome interactions. These advancements extend causal inference to dynamic and non-linear domains, offering new tools for understanding complex treatment effects in functional data settings.

Few-shot time series segmentation using prototype-defined infinite hidden Markov models

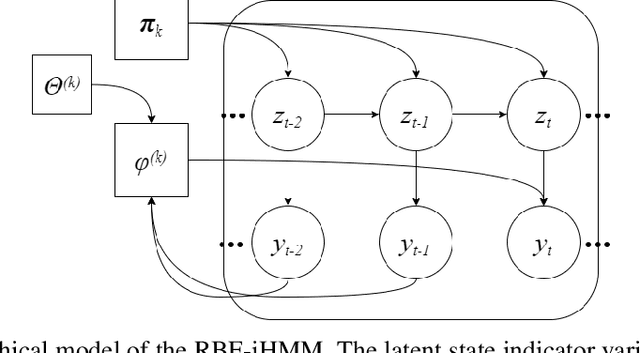
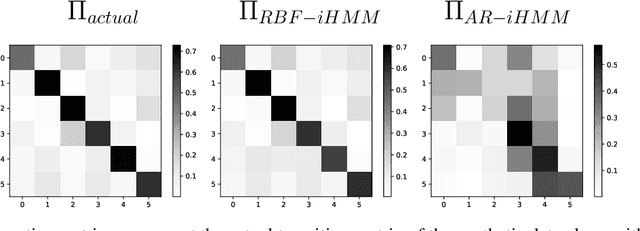
We propose a robust framework for interpretable, few-shot analysis of non-stationary sequential data based on flexible graphical models to express the structured distribution of sequential events, using prototype radial basis function (RBF) neural network emissions. A motivational link is demonstrated between prototypical neural network architectures for few-shot learning and the proposed RBF network infinite hidden Markov model (RBF-iHMM). We show that RBF networks can be efficiently specified via prototypes allowing us to express complex nonstationary patterns, while hidden Markov models are used to infer principled high-level Markov dynamics. The utility of the framework is demonstrated on biomedical signal processing applications such as automated seizure detection from EEG data where RBF networks achieve state-of-the-art performance using a fraction of the data needed to train long-short-term memory variational autoencoders.

Latent feature sharing: an adaptive approach to linear decomposition models

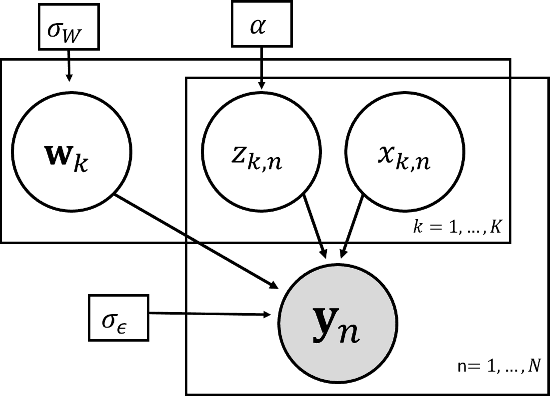
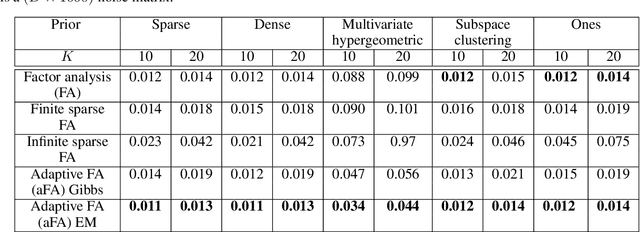
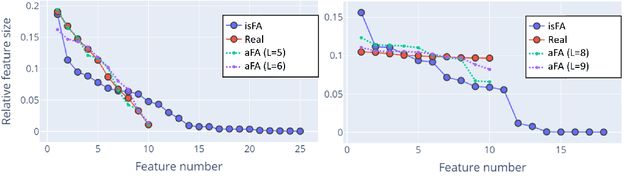
Latent feature models are canonical tools for exploratory analysis in classical and modern multivariate statistics. Many high-dimensional data can be approximated using a union of low-dimensional subspaces or factors. The allocation of data points to these latent factors itself typically uncovers key relationships in the input and helps us represent hidden causes explaining the data. A widely adopted view is to model feature allocation with discrete latent variables, where each data point is associated with a binary vector indicating latent features possessed by this data point. In this work we revise some of the issues with existing parametric and Bayesian nonparametric processes for feature allocation modelling and propose a novel framework that can capture wider set of feature allocation distributions. This new framework allows for explicit control over the number of features used to express each point and enables a more flexible set of allocation distributions including feature allocations with different sparsity levels. We use this approach to derive a novel adaptive Factor analysis (aFA), as well as, an adaptive probabilistic principle component analysis (aPPCA) capable of flexible structure discovery and dimensionality reduction in a wide case of scenarios. We derive both standard a Gibbs sampler, as well as, an expectation-maximization inference algorithms for aPPCA and aFA that converge orders of magnitude faster to a point estimate. We demonstrate that aFA can handle richer feature distributions, when compared to widely used sparse FA models and nonparametric FA models. We show that aPPCA and aFA can infer interpretable high level features both when applied on raw MNIST, when applied for interpreting autoencoder features. We also demonstrate an application of the aPPCA to more robust blind source separation for functional magnetic resonance imaging (fMRI).

Adaptive probabilistic principal component analysis

Using the linear Gaussian latent variable model as a starting point we relax some of the constraints it imposes by deriving a nonparametric latent feature Gaussian variable model. This model introduces additional discrete latent variables to the original structure. The Bayesian nonparametric nature of this new model allows it to adapt complexity as more data is observed and project each data point onto a varying number of subspaces. The linear relationship between the continuous latent and observed variables make the proposed model straightforward to interpret, resembling a locally adaptive probabilistic PCA (A-PPCA). We propose two alternative Gibbs sampling procedures for inference in the new model and demonstrate its applicability on sensor data for passive health monitoring.

Simple approximate MAP Inference for Dirichlet processes

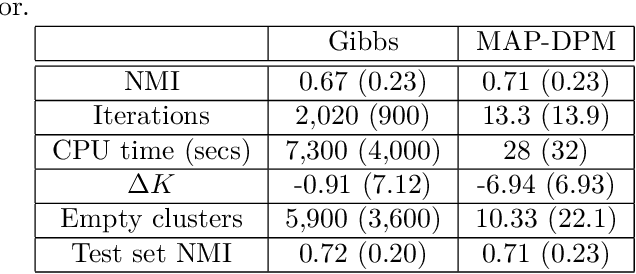
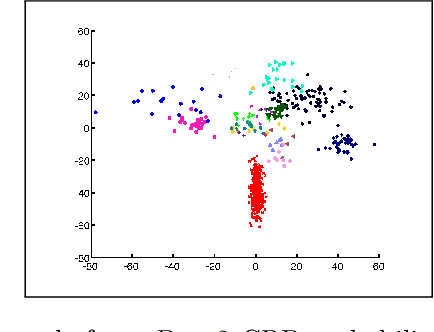
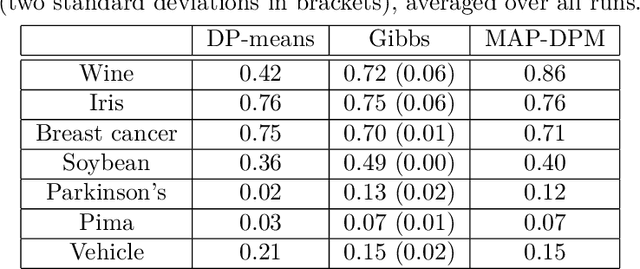
The Dirichlet process mixture (DPM) is a ubiquitous, flexible Bayesian nonparametric statistical model. However, full probabilistic inference in this model is analytically intractable, so that computationally intensive techniques such as Gibb's sampling are required. As a result, DPM-based methods, which have considerable potential, are restricted to applications in which computational resources and time for inference is plentiful. For example, they would not be practical for digital signal processing on embedded hardware, where computational resources are at a serious premium. Here, we develop simplified yet statistically rigorous approximate maximum a-posteriori (MAP) inference algorithms for DPMs. This algorithm is as simple as K-means clustering, performs in experiments as well as Gibb's sampling, while requiring only a fraction of the computational effort. Unlike related small variance asymptotics, our algorithm is non-degenerate and so inherits the "rich get richer" property of the Dirichlet process. It also retains a non-degenerate closed-form likelihood which enables standard tools such as cross-validation to be used. This is a well-posed approximation to the MAP solution of the probabilistic DPM model.