Deep-ICE: The first globally optimal algorithm for empirical risk minimization of two-layer maxout and ReLU networks

This paper introduces the first globally optimal algorithm for the empirical risk minimization problem of two-layer maxout and ReLU networks, i.e., minimizing the number of misclassifications. The algorithm has a worst-case time complexity of $O\left(N^{DK+1}\right)$, where $K$ denotes the number of hidden neurons and $D$ represents the number of features. It can be can be generalized to accommodate arbitrary computable loss functions without affecting its computational complexity. Our experiments demonstrate that the proposed algorithm provides provably exact solutions for small-scale datasets. To handle larger datasets, we introduce a novel coreset selection method that reduces the data size to a manageable scale, making it feasible for our algorithm. This extension enables efficient processing of large-scale datasets and achieves significantly improved performance, with a 20-30\% reduction in misclassifications for both training and prediction, compared to state-of-the-art approaches (neural networks trained using gradient descent and support vector machines), when applied to the same models (two-layer networks with fixed hidden nodes and linear models).

Provably optimal decision trees with arbitrary splitting rules in polynomial time

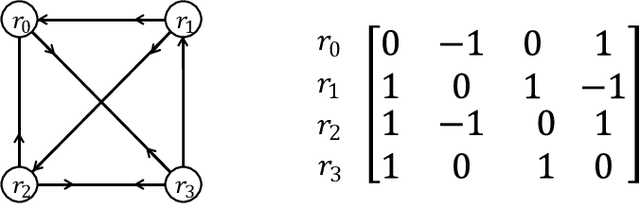
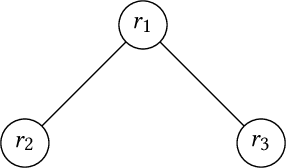
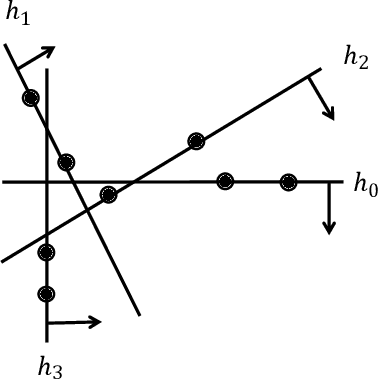
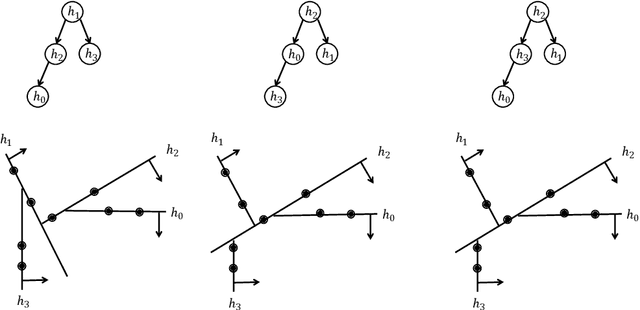
In this paper, we introduce a generic data structure called decision trees, which integrates several well-known data structures, including binary search trees, K-D trees, binary space partition trees, and decision tree models from machine learning. We provide the first axiomatic definition of decision trees. These axioms establish a firm mathematical foundation for studying decision tree problems. We refer to decision trees that satisfy the axioms as proper decision trees. We prove that only proper decision trees can be uniquely characterized as K-permutations. Since permutations are among the most well-studied combinatorial structures, this characterization provides a fundamental basis for analyzing the combinatorial and algorithmic properties of decision trees. As a result of this advancement, we develop the first provably correct polynomial-time algorithm for solving the optimal decision tree problem. Our algorithm is derived using a formal program derivation framework, which enables step-by-step equational reasoning to construct side-effect-free programs with guaranteed correctness. The derived algorithm is correct by construction and is applicable to decision tree problems defined by any splitting rules that adhere to the axioms and any objective functions that can be specified in a given form. Examples include the decision tree problems where splitting rules are defined by axis-parallel hyperplanes, arbitrary hyperplanes, and hypersurfaces. By extending the axioms, we can potentially address a broader range of problems. Moreover, the derived algorithm can easily accommodate various constraints, such as tree depth and leaf size, and is amenable to acceleration techniques such as thinning method.

Mechanism learning: Reverse causal inference in the presence of multiple unknown confounding through front-door causal bootstrapping

A major limitation of machine learning (ML) prediction models is that they recover associational, rather than causal, predictive relationships between variables. In high-stakes automation applications of ML this is problematic, as the model often learns spurious, non-causal associations. This paper proposes mechanism learning, a simple method which uses front-door causal bootstrapping to deconfound observational data such that any appropriate ML model is forced to learn predictive relationships between effects and their causes (reverse causal inference), despite the potential presence of multiple unknown and unmeasured confounding. Effect variables can be very high dimensional, and the predictive relationship nonlinear, as is common in ML applications. This novel method is widely applicable, the only requirement is the existence of a mechanism variable mediating the cause (prediction target) and effect (feature data), which is independent of the (unmeasured) confounding variables. We test our method on fully synthetic, semi-synthetic and real-world datasets, demonstrating that it can discover reliable, unbiased, causal ML predictors where by contrast, the same ML predictor trained naively using classical supervised learning on the original observational data, is heavily biased by spurious associations. We provide code to implement the results in the paper, online.

EKM: An exact, polynomial-time algorithm for the $K$-medoids problem

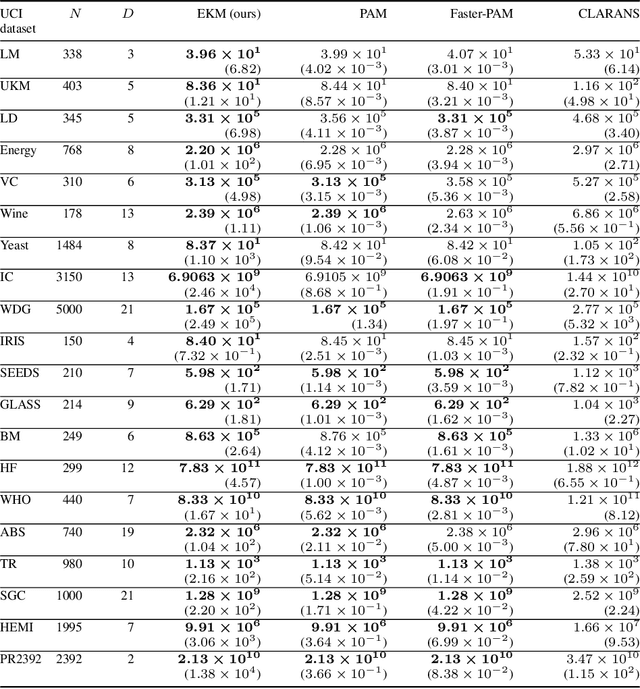
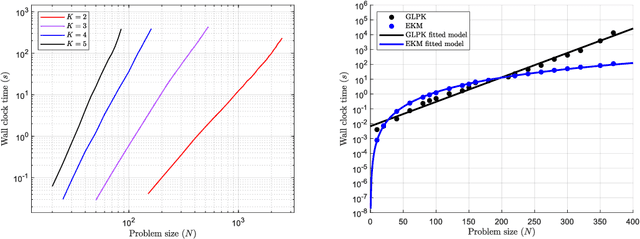
The $K$-medoids problem is a challenging combinatorial clustering task, widely used in data analysis applications. While numerous algorithms have been proposed to solve this problem, none of these are able to obtain an exact (globally optimal) solution for the problem in polynomial time. In this paper, we present EKM: a novel algorithm for solving this problem exactly with worst-case $O\left(N^{K+1}\right)$ time complexity. EKM is developed according to recent advances in transformational programming and combinatorial generation, using formal program derivation steps. The derived algorithm is provably correct by construction. We demonstrate the effectiveness of our algorithm by comparing it against various approximate methods on numerous real-world datasets. We show that the wall-clock run time of our algorithm matches the worst-case time complexity analysis on synthetic datasets, clearly outperforming the exponential time complexity of benchmark branch-and-bound based MIP solvers. To our knowledge, this is the first, rigorously-proven polynomial time, practical algorithm for this ubiquitous problem.

Algorithmic syntactic causal identification

Causal identification in causal Bayes nets (CBNs) is an important tool in causal inference allowing the derivation of interventional distributions from observational distributions where this is possible in principle. However, most existing formulations of causal identification using techniques such as d-separation and do-calculus are expressed within the mathematical language of classical probability theory on CBNs. However, there are many causal settings where probability theory and hence current causal identification techniques are inapplicable such as relational databases, dataflow programs such as hardware description languages, distributed systems and most modern machine learning algorithms. We show that this restriction can be lifted by replacing the use of classical probability theory with the alternative axiomatic foundation of symmetric monoidal categories. In this alternative axiomatization, we show how an unambiguous and clean distinction can be drawn between the general syntax of causal models and any specific semantic implementation of that causal model. This allows a purely syntactic algorithmic description of general causal identification by a translation of recent formulations of the general ID algorithm through fixing. Our description is given entirely in terms of the non-parametric ADMG structure specifying a causal model and the algebraic signature of the corresponding monoidal category, to which a sequence of manipulations is then applied so as to arrive at a modified monoidal category in which the desired, purely syntactic interventional causal model, is obtained. We use this idea to derive purely syntactic analogues of classical back-door and front-door causal adjustment, and illustrate an application to a more complex causal model.

An efficient, provably exact algorithm for the 0-1 loss linear classification problem

Algorithms for solving the linear classification problem have a long history, dating back at least to 1936 with linear discriminant analysis. For linearly separable data, many algorithms can obtain the exact solution to the corresponding 0-1 loss classification problem efficiently, but for data which is not linearly separable, it has been shown that this problem, in full generality, is NP-hard. Alternative approaches all involve approximations of some kind, including the use of surrogates for the 0-1 loss (for example, the hinge or logistic loss) or approximate combinatorial search, none of which can be guaranteed to solve the problem exactly. Finding efficient algorithms to obtain an exact i.e. globally optimal solution for the 0-1 loss linear classification problem with fixed dimension, remains an open problem. In research we report here, we detail the construction of a new algorithm, incremental cell enumeration (ICE), that can solve the 0-1 loss classification problem exactly in polynomial time. To our knowledge, this is the first, rigorously-proven polynomial time algorithm for this long-standing problem.

Patient-Specific Game-Based Transfer Method for Parkinson's Disease Severity Prediction

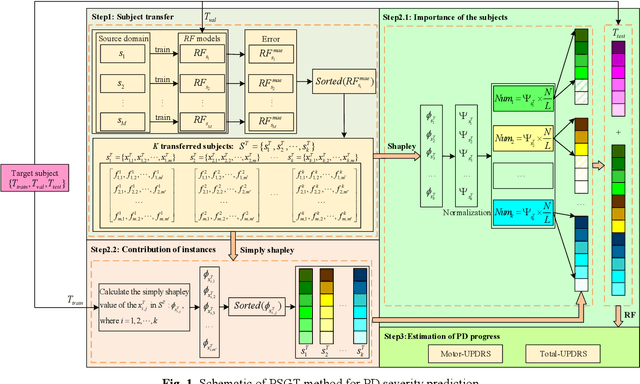
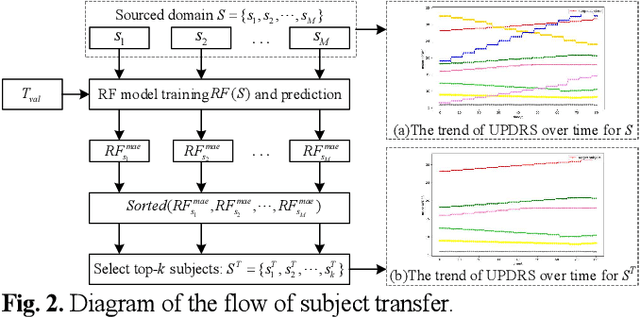
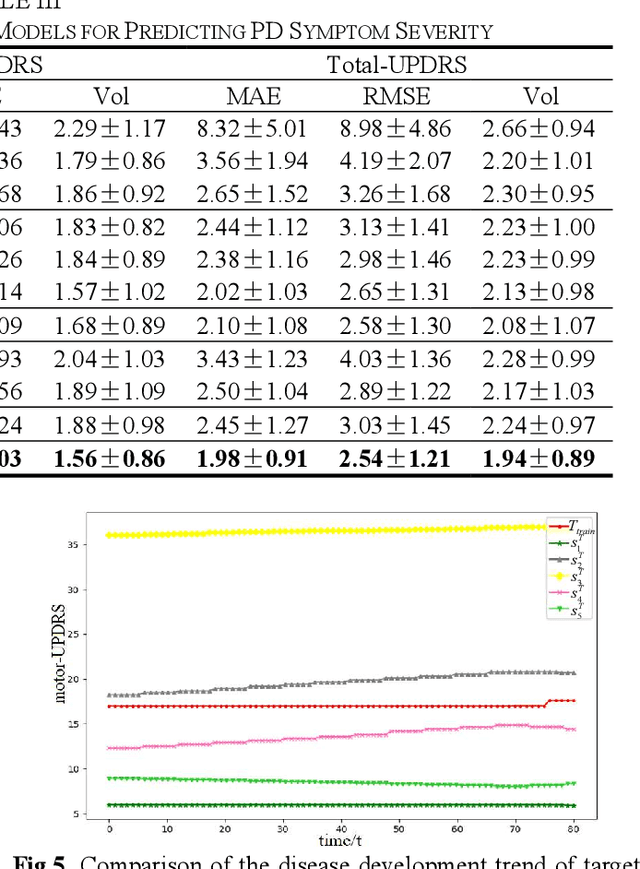
Dysphonia is one of the early symptoms of Parkinson's disease (PD). Most existing methods use feature selection methods to find the optimal subset of voice features for all PD patients. Few have considered the heterogeneity between patients, which implies the need to provide specific prediction models for different patients. However, building the specific model faces the challenge of small sample size, which makes it lack generalization ability. Instance transfer is an effective way to solve this problem. Therefore, this paper proposes a patient-specific game-based transfer (PSGT) method for PD severity prediction. First, a selection mechanism is used to select PD patients with similar disease trends to the target patient from the source domain, which greatly reduces the risk of negative transfer. Then, the contribution of the transferred subjects and their instances to the disease estimation of the target subject is fairly evaluated by the Shapley value, which improves the interpretability of the method. Next, the proportion of valid instances in the transferred subjects is determined, and the instances with higher contribution are transferred to further reduce the difference between the transferred instance subset and the target subject. Finally, the selected subset of instances is added to the training set of the target subject, and the extended data is fed into the random forest to improve the performance of the method. Parkinson's telemonitoring dataset is used to evaluate the feasibility and effectiveness. Experiment results show that the PSGT has better performance in both prediction error and stability over compared methods.

Polymorphic dynamic programming by algebraic shortcut fusion

Dynamic programming (DP) is a broadly applicable algorithmic design paradigm for the efficient, exact solution of otherwise intractable, combinatorial problems. However, the design of such algorithms is often presented informally in an ad-hoc manner, and as a result is often difficult to apply correctly. In this paper, we present a rigorous algebraic formalism for systematically deriving novel DP algorithms, either from existing DP algorithms or from simple functional recurrences. These derivations lead to algorithms which are provably correct and polymorphic over any semiring, which means that they can be applied to the full scope of combinatorial problems expressible in terms of semirings. This includes, for example: optimization, optimal probability and Viterbi decoding, probabilistic marginalization, logical inference, fuzzy sets, differentiable softmax, and relational and provenance queries. The approach, building on many ideas from the existing literature on constructive algorithmics, exploits generic properties of (semiring) polymorphic functions, tupling and formal sums (lifting), and algebraic simplifications arising from constraint algebras. We demonstrate the effectiveness of this formalism for some example applications arising in signal processing, bioinformatics and reliability engineering.

Few-shot time series segmentation using prototype-defined infinite hidden Markov models

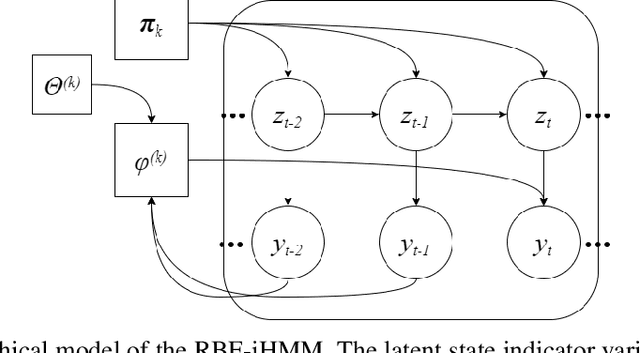
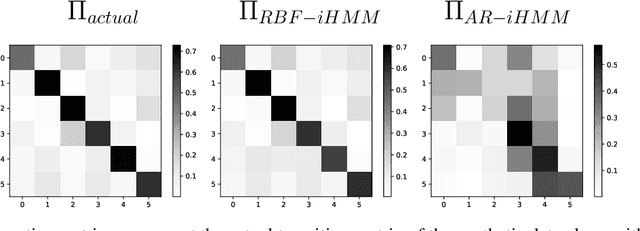
We propose a robust framework for interpretable, few-shot analysis of non-stationary sequential data based on flexible graphical models to express the structured distribution of sequential events, using prototype radial basis function (RBF) neural network emissions. A motivational link is demonstrated between prototypical neural network architectures for few-shot learning and the proposed RBF network infinite hidden Markov model (RBF-iHMM). We show that RBF networks can be efficiently specified via prototypes allowing us to express complex nonstationary patterns, while hidden Markov models are used to infer principled high-level Markov dynamics. The utility of the framework is demonstrated on biomedical signal processing applications such as automated seizure detection from EEG data where RBF networks achieve state-of-the-art performance using a fraction of the data needed to train long-short-term memory variational autoencoders.

Latent feature sharing: an adaptive approach to linear decomposition models

Latent feature models are canonical tools for exploratory analysis in classical and modern multivariate statistics. Many high-dimensional data can be approximated using a union of low-dimensional subspaces or factors. The allocation of data points to these latent factors itself typically uncovers key relationships in the input and helps us represent hidden causes explaining the data. A widely adopted view is to model feature allocation with discrete latent variables, where each data point is associated with a binary vector indicating latent features possessed by this data point. In this work we revise some of the issues with existing parametric and Bayesian nonparametric processes for feature allocation modelling and propose a novel framework that can capture wider set of feature allocation distributions. This new framework allows for explicit control over the number of features used to express each point and enables a more flexible set of allocation distributions including feature allocations with different sparsity levels. We use this approach to derive a novel adaptive Factor analysis (aFA), as well as, an adaptive probabilistic principle component analysis (aPPCA) capable of flexible structure discovery and dimensionality reduction in a wide case of scenarios. We derive both standard a Gibbs sampler, as well as, an expectation-maximization inference algorithms for aPPCA and aFA that converge orders of magnitude faster to a point estimate. We demonstrate that aFA can handle richer feature distributions, when compared to widely used sparse FA models and nonparametric FA models. We show that aPPCA and aFA can infer interpretable high level features both when applied on raw MNIST, when applied for interpreting autoencoder features. We also demonstrate an application of the aPPCA to more robust blind source separation for functional magnetic resonance imaging (fMRI).