EKM: An exact, polynomial-time algorithm for the $K$-medoids problem
Paper and Code
May 16, 2024
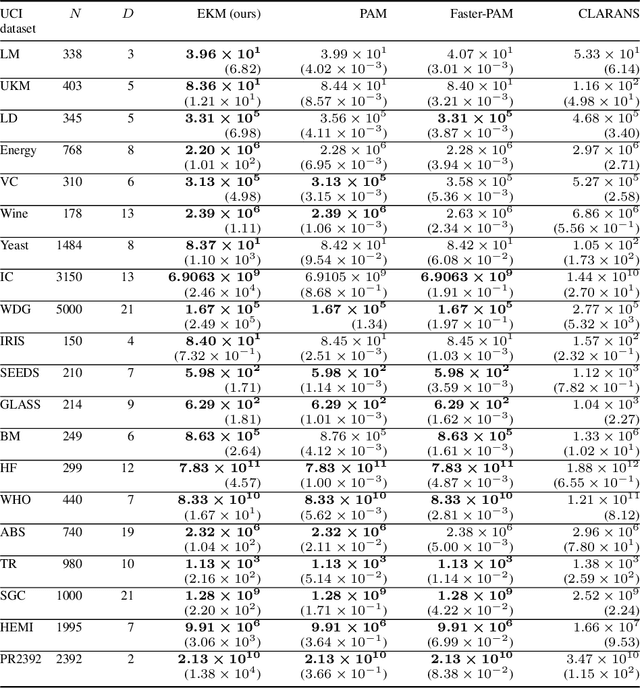
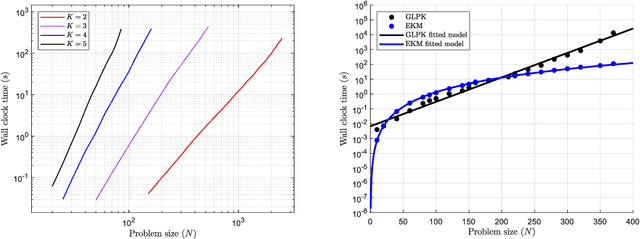
The $K$-medoids problem is a challenging combinatorial clustering task, widely used in data analysis applications. While numerous algorithms have been proposed to solve this problem, none of these are able to obtain an exact (globally optimal) solution for the problem in polynomial time. In this paper, we present EKM: a novel algorithm for solving this problem exactly with worst-case $O\left(N^{K+1}\right)$ time complexity. EKM is developed according to recent advances in transformational programming and combinatorial generation, using formal program derivation steps. The derived algorithm is provably correct by construction. We demonstrate the effectiveness of our algorithm by comparing it against various approximate methods on numerous real-world datasets. We show that the wall-clock run time of our algorithm matches the worst-case time complexity analysis on synthetic datasets, clearly outperforming the exponential time complexity of benchmark branch-and-bound based MIP solvers. To our knowledge, this is the first, rigorously-proven polynomial time, practical algorithm for this ubiquitous problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge