Symmetry-driven embedding of networks in hyperbolic space

Hyperbolic models can reproduce the heavy-tailed degree distribution, high clustering, and hierarchical structure of empirical networks. Current algorithms for finding the hyperbolic coordinates of networks, however, do not quantify uncertainty in the inferred coordinates. We present BIGUE, a Markov chain Monte Carlo (MCMC) algorithm that samples the posterior distribution of a Bayesian hyperbolic random graph model. We show that combining random walk and random cluster transformations significantly improves mixing compared to the commonly used and state-of-the-art dynamic Hamiltonian Monte Carlo algorithm. Using this algorithm, we also provide evidence that the posterior distribution cannot be approximated by a multivariate normal distribution, thereby justifying the use of MCMC to quantify the uncertainty of the inferred parameters.

Exact and rapid linear clustering of networks with dynamic programming

We study the problem of clustering networks whose nodes have imputed or physical positions in a single dimension, such as prestige hierarchies or the similarity dimension of hyperbolic embeddings. Existing algorithms, such as the critical gap method and other greedy strategies, only offer approximate solutions. Here, we introduce a dynamic programming approach that returns provably optimal solutions in polynomial time -- O(n^2) steps -- for a broad class of clustering objectives. We demonstrate the algorithm through applications to synthetic and empirical networks, and show that it outperforms existing heuristics by a significant margin, with a similar execution time.

Deep learning of stochastic contagion dynamics on complex networks

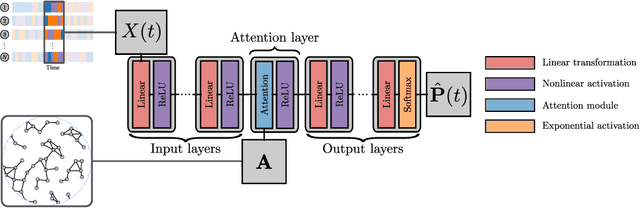
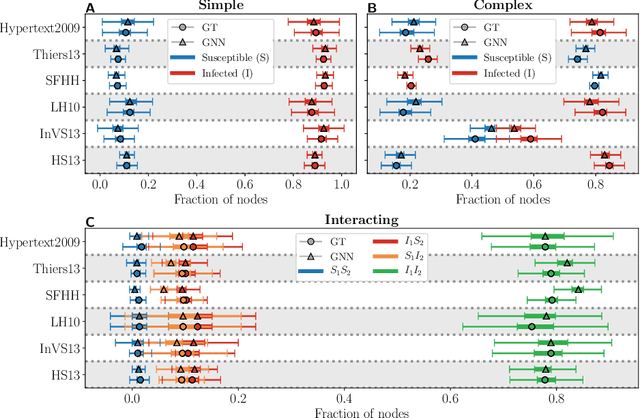
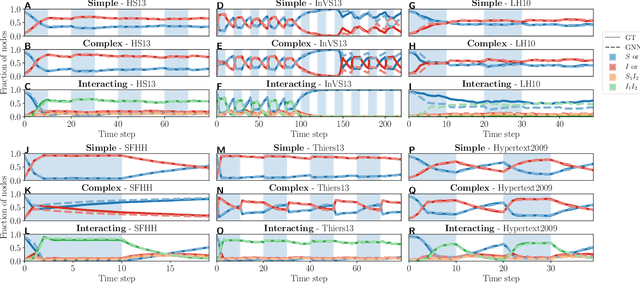
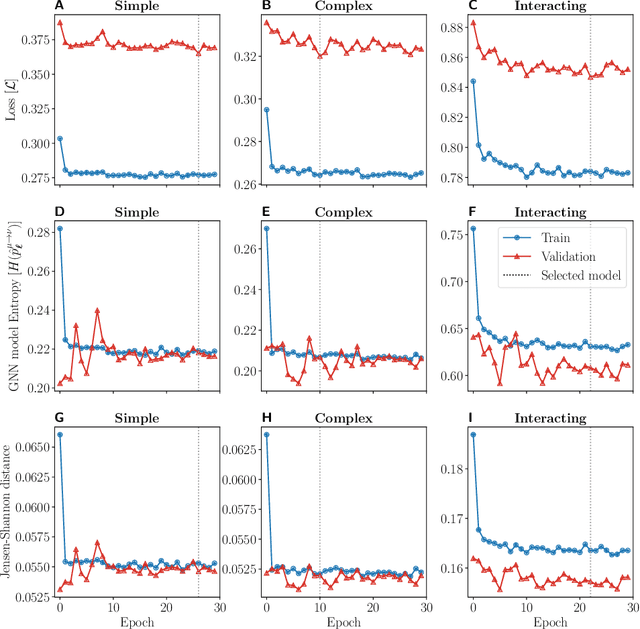
Forecasting the evolution of contagion dynamics is still an open problem to which mechanistic models only offer a partial answer. To remain mathematically and/or computationally tractable, these models must rely on simplifying assumptions, thereby limiting the quantitative accuracy of their predictions and the complexity of the dynamics they can model. Here, we propose a complementary approach based on deep learning where the effective local mechanisms governing a dynamic are learned automatically from time series data. Our graph neural network architecture makes very few assumptions about the dynamics, and we demonstrate its accuracy using stochastic contagion dynamics of increasing complexity on static and temporal networks. By allowing simulations on arbitrary network structures, our approach makes it possible to explore the properties of the learned dynamics beyond the training data. Our results demonstrate how deep learning offers a new and complementary perspective to build effective models of contagion dynamics on networks.

Mercator: uncovering faithful hyperbolic embeddings of complex networks

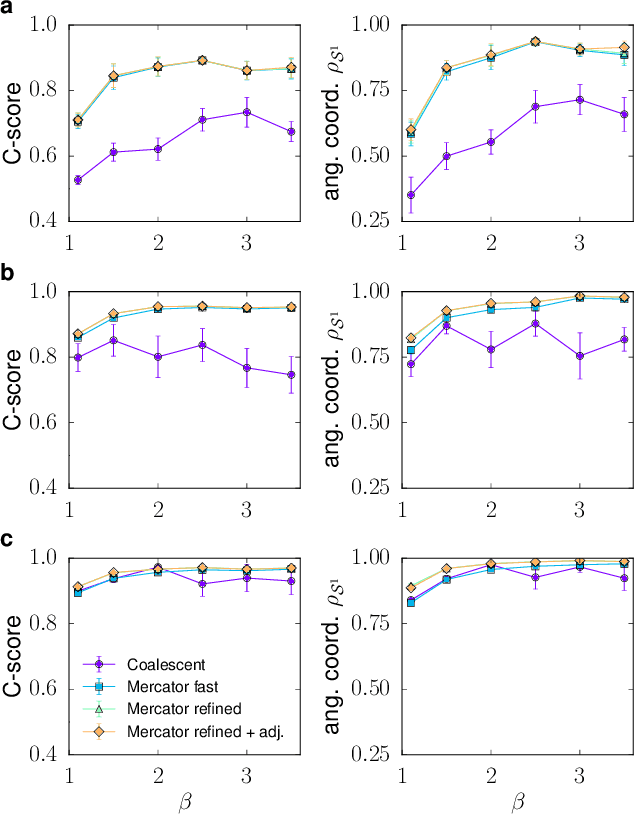
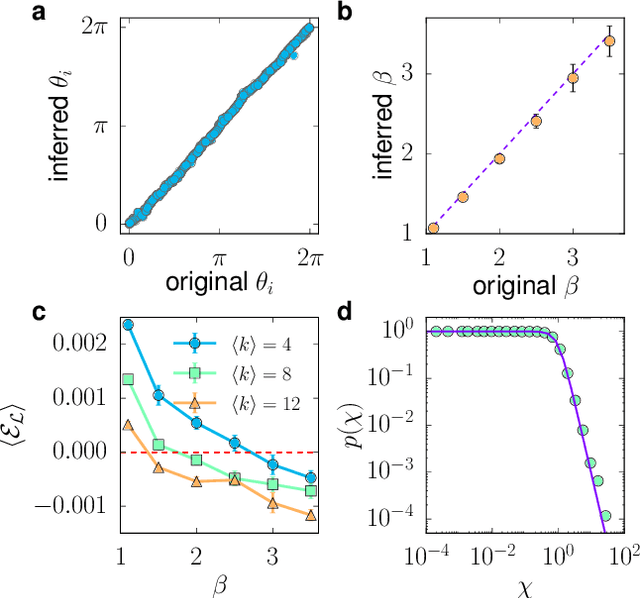
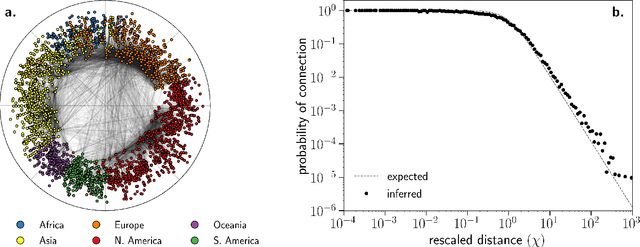
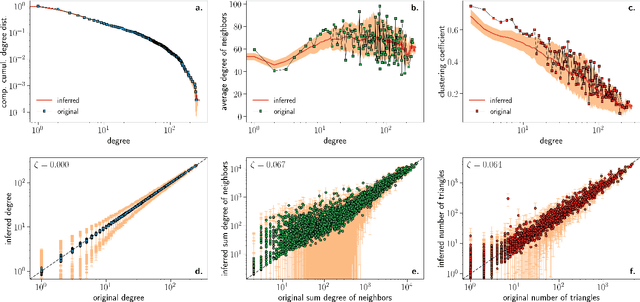
We introduce Mercator, a reliable embedding method to map real complex networks into their hyperbolic latent geometry. The method assumes that the structure of networks is well described by the Popularity$\times$Similarity $\mathbb{S}^1/\mathbb{H}^2$ static geometric network model, which can accommodate arbitrary degree distributions and reproduces many pivotal properties of real networks, including self-similarity patterns. The algorithm mixes machine learning and maximum likelihood approaches to infer the coordinates of the nodes in the underlying hyperbolic disk with the best matching between the observed network topology and the geometric model. In its fast mode, Mercator uses a model-adjusted machine learning technique performing dimensional reduction to produce a fast and accurate map, whose quality already outperform other embedding algorithms in the literature. In the refined Mercator mode, the fast-mode embedding result is taken as an initial condition in a Maximum Likelihood estimation, which significantly improves the quality of the final embedding. Apart from its accuracy as an embedding tool, Mercator has the clear advantage of systematically inferring not only node orderings, or angular positions, but also the hidden degrees and global model parameters, and has the ability to embed networks with arbitrary degree distributions. Overall, our results suggest that mixing machine learning and maximum likelihood techniques in a model-dependent framework can boost the meaningful mapping of complex networks.