Network representations reveal structured uncertainty in music

Music, as a structured yet perceptually rich experience, can be modeled as a network to uncover how humans encode and process auditory information. While network-based representations of music are increasingly common, the impact of feature selection on structural properties and cognitive alignment remains underexplored. In this study, we evaluated eight network models, each constructed from symbolic representations of piano compositions using distinct combinations of pitch, octave, duration, and interval, designed to be representative of existing approaches in the literature. By comparing these models through topological metrics, entropy analysis, and divergence with respect to inferred cognitive representations, we assessed both their structural and perceptual efficiency. Our findings reveal that simpler, feature-specific models better match human perception, whereas complex, multidimensional representations introduce cognitive inefficiencies. These results support the view that humans rely on modular, parallel cognitive networks--an architecture consistent with theories of predictive processing and free energy minimization. Moreover, we find that musical networks are structurally organized to guide attention toward transitions that are both uncertain and inferable. The resulting structure concentrates uncertainty in a few frequently visited nodes, creating local entropy gradients that alternate between stable and unpredictable regions, thereby enabling the expressive dynamics of tension and release that define the musical experience. These findings show that network structures make the organization of uncertainty in music observable, offering new insight into how patterned flows of expectation shape perception, and open new directions for studying how musical structures evolve across genres, cultures, and historical periods through the lens of network science.

Task complexity shapes internal representations and robustness in neural networks

Neural networks excel across a wide range of tasks, yet remain black boxes. In particular, how their internal representations are shaped by the complexity of the input data and the problems they solve remains obscure. In this work, we introduce a suite of five data-agnostic probes-pruning, binarization, noise injection, sign flipping, and bipartite network randomization-to quantify how task difficulty influences the topology and robustness of representations in multilayer perceptrons (MLPs). MLPs are represented as signed, weighted bipartite graphs from a network science perspective. We contrast easy and hard classification tasks on the MNIST and Fashion-MNIST datasets. We show that binarizing weights in hard-task models collapses accuracy to chance, whereas easy-task models remain robust. We also find that pruning low-magnitude edges in binarized hard-task models reveals a sharp phase-transition in performance. Moreover, moderate noise injection can enhance accuracy, resembling a stochastic-resonance effect linked to optimal sign flips of small-magnitude weights. Finally, preserving only the sign structure-instead of precise weight magnitudes-through bipartite network randomizations suffices to maintain high accuracy. These phenomena define a model- and modality-agnostic measure of task complexity: the performance gap between full-precision and binarized or shuffled neural network performance. Our findings highlight the crucial role of signed bipartite topology in learned representations and suggest practical strategies for model compression and interpretability that align with task complexity.

Hyperbolic Benchmarking Unveils Network Topology-Feature Relationship in GNN Performance

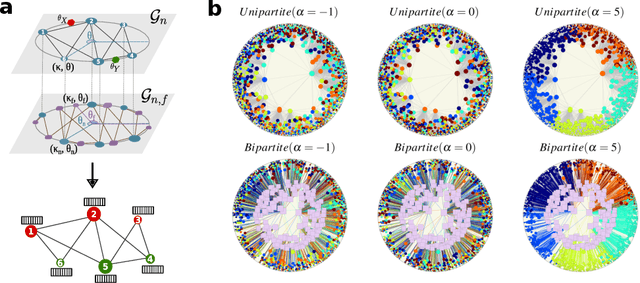
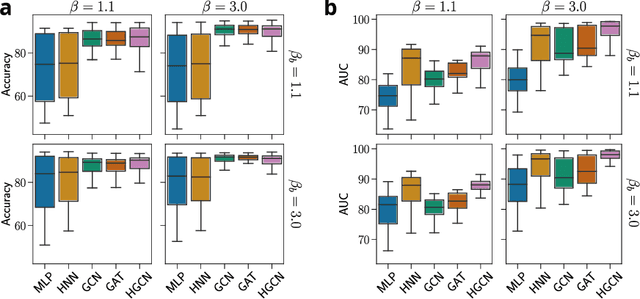
Graph Neural Networks (GNNs) have excelled in predicting graph properties in various applications ranging from identifying trends in social networks to drug discovery and malware detection. With the abundance of new architectures and increased complexity, GNNs are becoming highly specialized when tested on a few well-known datasets. However, how the performance of GNNs depends on the topological and features properties of graphs is still an open question. In this work, we introduce a comprehensive benchmarking framework for graph machine learning, focusing on the performance of GNNs across varied network structures. Utilizing the geometric soft configuration model in hyperbolic space, we generate synthetic networks with realistic topological properties and node feature vectors. This approach enables us to assess the impact of network properties, such as topology-feature correlation, degree distributions, local density of triangles (or clustering), and homophily, on the effectiveness of different GNN architectures. Our results highlight the dependency of model performance on the interplay between network structure and node features, providing insights for model selection in various scenarios. This study contributes to the field by offering a versatile tool for evaluating GNNs, thereby assisting in developing and selecting suitable models based on specific data characteristics.

Mercator: uncovering faithful hyperbolic embeddings of complex networks

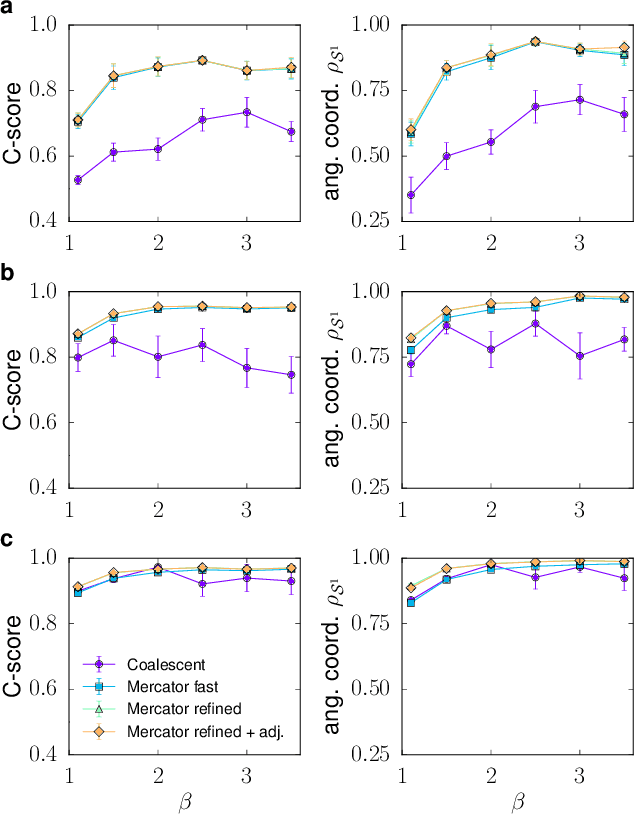
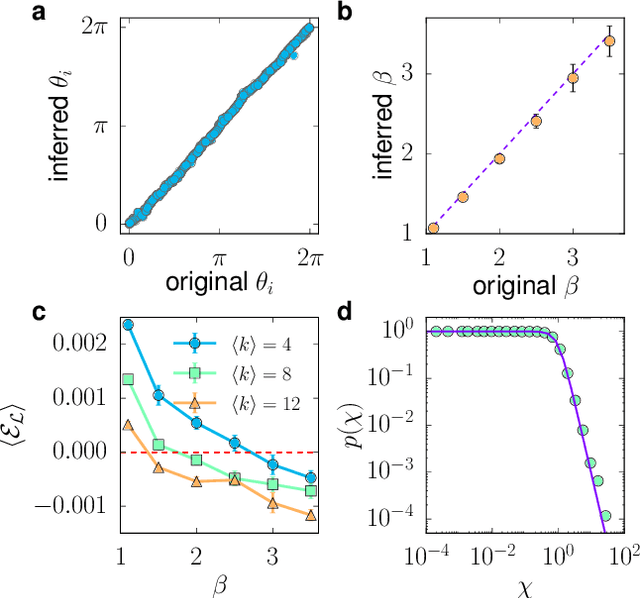
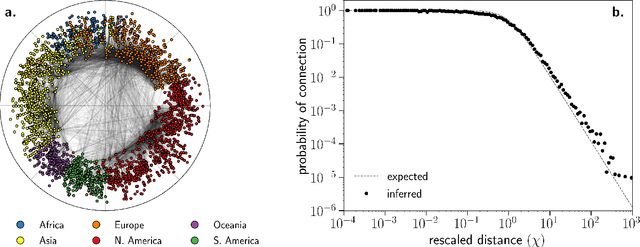
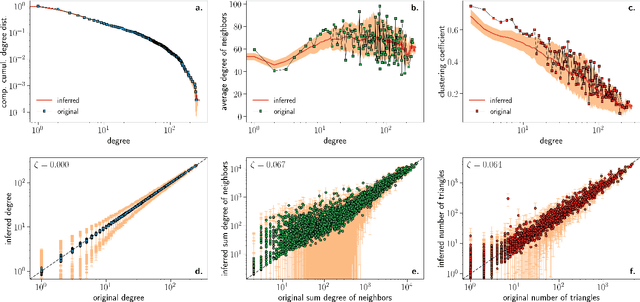
We introduce Mercator, a reliable embedding method to map real complex networks into their hyperbolic latent geometry. The method assumes that the structure of networks is well described by the Popularity$\times$Similarity $\mathbb{S}^1/\mathbb{H}^2$ static geometric network model, which can accommodate arbitrary degree distributions and reproduces many pivotal properties of real networks, including self-similarity patterns. The algorithm mixes machine learning and maximum likelihood approaches to infer the coordinates of the nodes in the underlying hyperbolic disk with the best matching between the observed network topology and the geometric model. In its fast mode, Mercator uses a model-adjusted machine learning technique performing dimensional reduction to produce a fast and accurate map, whose quality already outperform other embedding algorithms in the literature. In the refined Mercator mode, the fast-mode embedding result is taken as an initial condition in a Maximum Likelihood estimation, which significantly improves the quality of the final embedding. Apart from its accuracy as an embedding tool, Mercator has the clear advantage of systematically inferring not only node orderings, or angular positions, but also the hidden degrees and global model parameters, and has the ability to embed networks with arbitrary degree distributions. Overall, our results suggest that mixing machine learning and maximum likelihood techniques in a model-dependent framework can boost the meaningful mapping of complex networks.