Link prediction with continuous-time classical and quantum walks

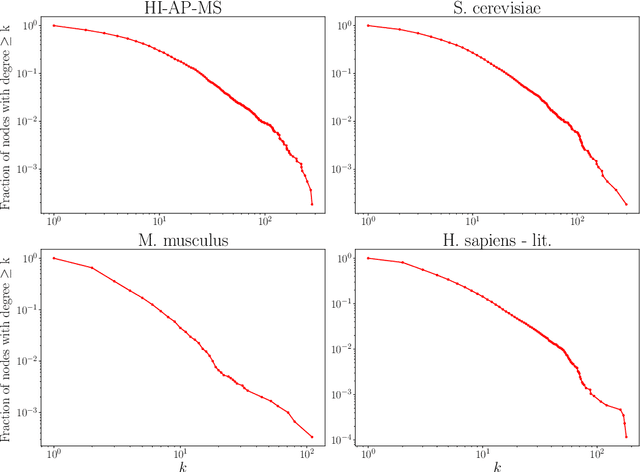
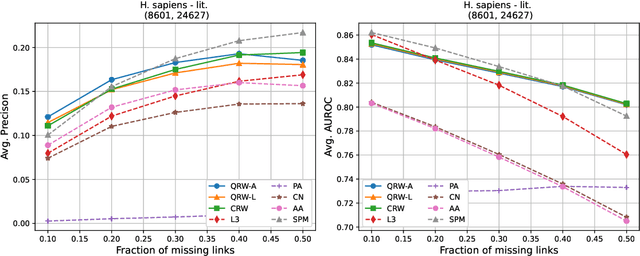
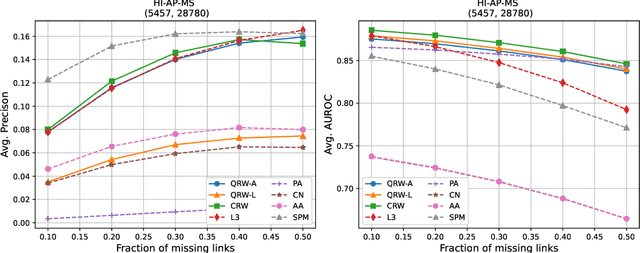
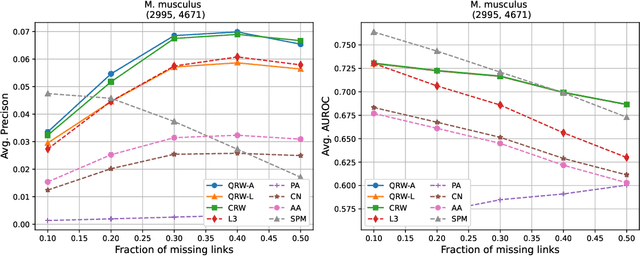
Protein-protein interaction (PPI) networks consist of the physical and/or functional interactions between the proteins of an organism. Since the biophysical and high-throughput methods used to form PPI networks are expensive, time-consuming, and often contain inaccuracies, the resulting networks are usually incomplete. In order to infer missing interactions in these networks, we propose a novel class of link prediction methods based on continuous-time classical and quantum random walks. In the case of quantum walks, we examine the usage of both the network adjacency and Laplacian matrices for controlling the walk dynamics. We define a score function based on the corresponding transition probabilities and perform tests on four real-world PPI datasets. Our results show that continuous-time classical random walks and quantum walks using the network adjacency matrix can successfully predict missing protein-protein interactions, with performance rivalling the state of the art.

Mercator: uncovering faithful hyperbolic embeddings of complex networks

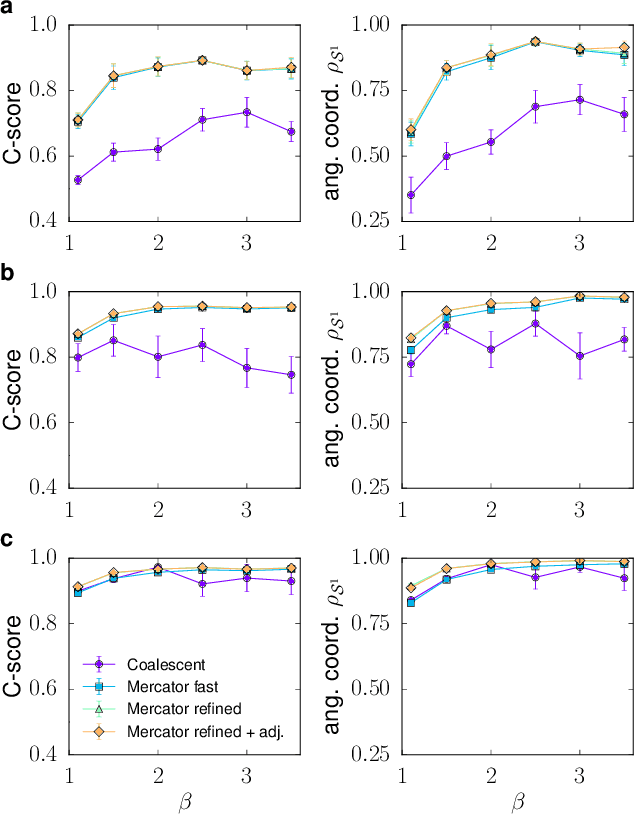
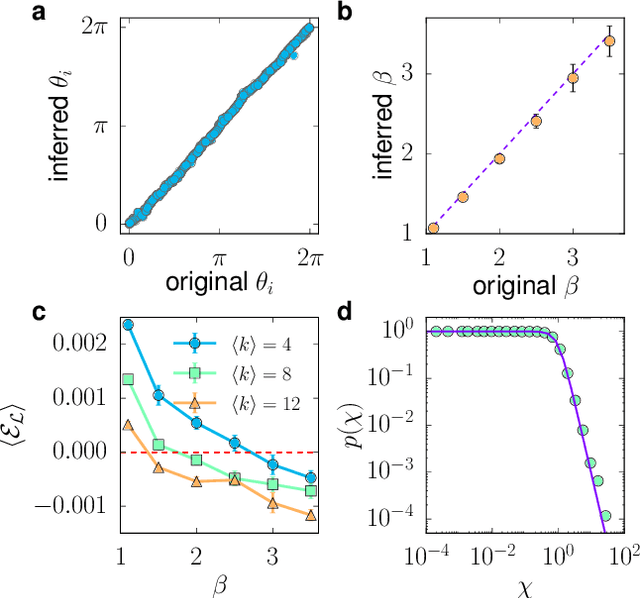
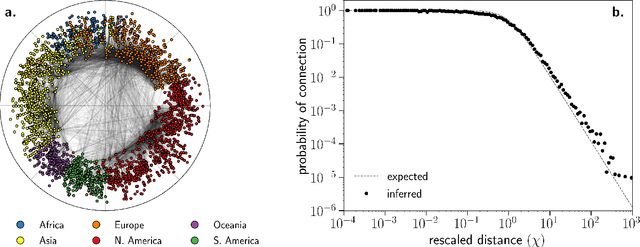
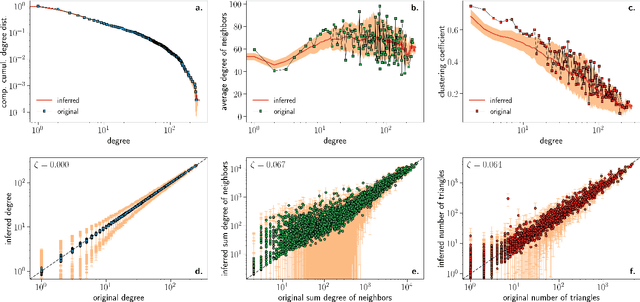
We introduce Mercator, a reliable embedding method to map real complex networks into their hyperbolic latent geometry. The method assumes that the structure of networks is well described by the Popularity$\times$Similarity $\mathbb{S}^1/\mathbb{H}^2$ static geometric network model, which can accommodate arbitrary degree distributions and reproduces many pivotal properties of real networks, including self-similarity patterns. The algorithm mixes machine learning and maximum likelihood approaches to infer the coordinates of the nodes in the underlying hyperbolic disk with the best matching between the observed network topology and the geometric model. In its fast mode, Mercator uses a model-adjusted machine learning technique performing dimensional reduction to produce a fast and accurate map, whose quality already outperform other embedding algorithms in the literature. In the refined Mercator mode, the fast-mode embedding result is taken as an initial condition in a Maximum Likelihood estimation, which significantly improves the quality of the final embedding. Apart from its accuracy as an embedding tool, Mercator has the clear advantage of systematically inferring not only node orderings, or angular positions, but also the hidden degrees and global model parameters, and has the ability to embed networks with arbitrary degree distributions. Overall, our results suggest that mixing machine learning and maximum likelihood techniques in a model-dependent framework can boost the meaningful mapping of complex networks.