Deep learning of stochastic contagion dynamics on complex networks

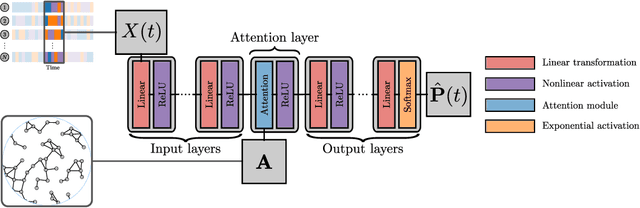
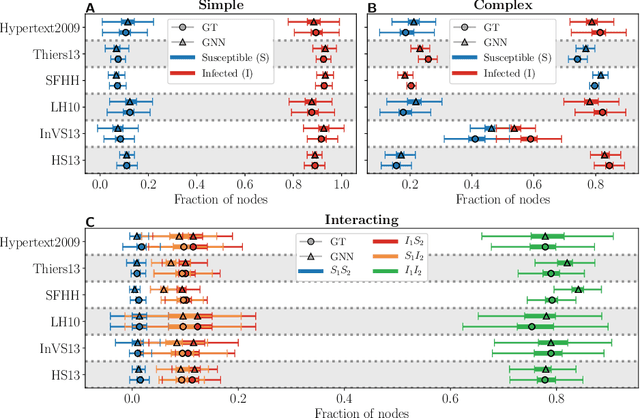
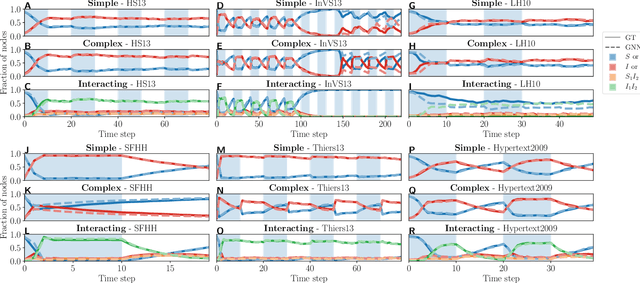
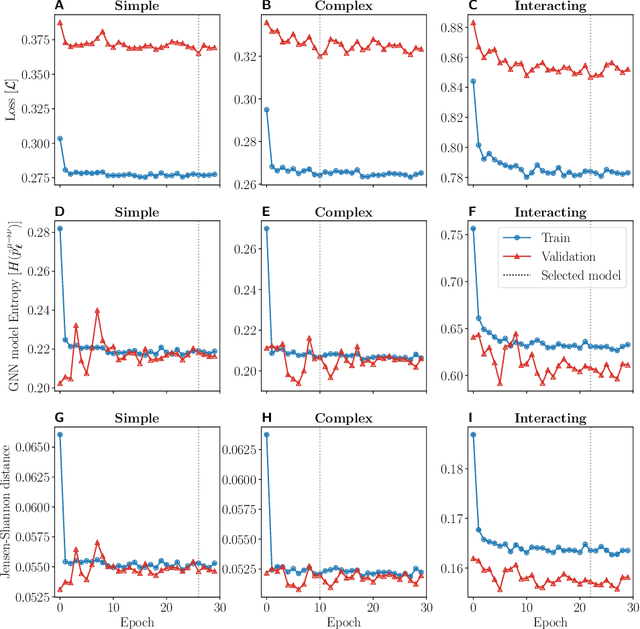
Forecasting the evolution of contagion dynamics is still an open problem to which mechanistic models only offer a partial answer. To remain mathematically and/or computationally tractable, these models must rely on simplifying assumptions, thereby limiting the quantitative accuracy of their predictions and the complexity of the dynamics they can model. Here, we propose a complementary approach based on deep learning where the effective local mechanisms governing a dynamic are learned automatically from time series data. Our graph neural network architecture makes very few assumptions about the dynamics, and we demonstrate its accuracy using stochastic contagion dynamics of increasing complexity on static and temporal networks. By allowing simulations on arbitrary network structures, our approach makes it possible to explore the properties of the learned dynamics beyond the training data. Our results demonstrate how deep learning offers a new and complementary perspective to build effective models of contagion dynamics on networks.

Detecting structural perturbations from time series with deep learning

Small disturbances can trigger functional breakdowns in complex systems. A challenging task is to infer the structural cause of a disturbance in a networked system, soon enough to prevent a catastrophe. We present a graph neural network approach, borrowed from the deep learning paradigm, to infer structural perturbations from functional time series. We show our data-driven approach outperforms typical reconstruction methods while meeting the accuracy of Bayesian inference. We validate the versatility and performance of our approach with epidemic spreading, population dynamics, and neural dynamics, on various network structures: random networks, scale-free networks, 25 real food-web systems, and the C. Elegans connectome. Moreover, we report that our approach is robust to data corruption. This work uncovers a practical avenue to study the resilience of real-world complex systems.

Network archaeology: phase transition in the recoverability of network history

Network growth processes can be understood as generative models of the structure and history of complex networks. This point of view naturally leads to the problem of network archaeology: Reconstructing all the past states of a network from its structure---a difficult permutation inference problem. In this paper, we introduce a Bayesian formulation of network archaeology, with a generalization of preferential attachment as our generative mechanism. We develop a sequential importance sampling algorithm to evaluate the posterior averages of this model, as well as an efficient heuristic that uncovers the history of a network in linear time. We use these methods to identify and characterize a phase transition in the quality of the reconstructed history, when they are applied to artificial networks generated by the model itself. Despite the existence of a no-recovery phase, we find that non-trivial inference is possible in a large portion of the parameter space as well as on empirical data.