Multilayer Networks for Text Analysis with Multiple Data Types

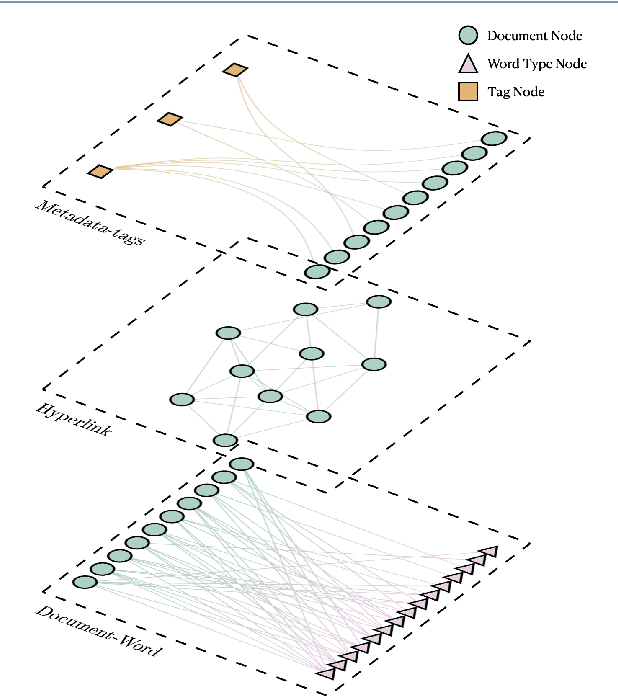
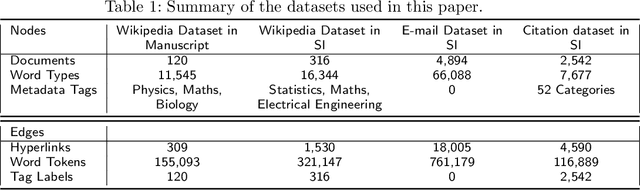
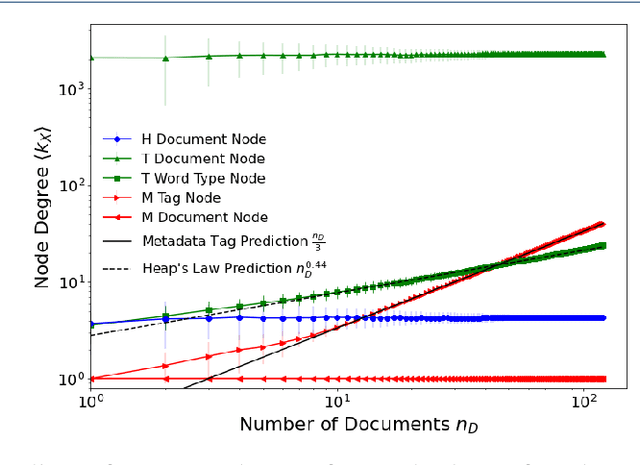
We are interested in the widespread problem of clustering documents and finding topics in large collections of written documents in the presence of metadata and hyperlinks. To tackle the challenge of accounting for these different types of datasets, we propose a novel framework based on Multilayer Networks and Stochastic Block Models. The main innovation of our approach over other techniques is that it applies the same non-parametric probabilistic framework to the different sources of datasets simultaneously. The key difference to other multilayer complex networks is the strong unbalance between the layers, with the average degree of different node types scaling differently with system size. We show that the latter observation is due to generic properties of text, such as Heaps' law, and strongly affects the inference of communities. We present and discuss the performance of our method in different datasets (hundreds of Wikipedia documents, thousands of scientific papers, and thousands of E-mails) showing that taking into account multiple types of information provides a more nuanced view on topic- and document-clusters and increases the ability to predict missing links.

Additive Poisson Process: Learning Intensity of Higher-Order Interaction in Stochastic Processes

We present the Additive Poisson Process (APP), a novel framework that can model the higher-order interaction effects of the intensity functions in stochastic processes using lower dimensional projections. Our model combines the techniques in information geometry to model higher-order interactions on a statistical manifold and in generalized additive models to use lower-dimensional projections to overcome the effects from the curse of dimensionality. Our approach solves a convex optimization problem by minimizing the KL divergence from a sample distribution in lower dimensional projections to the distribution modeled by an intensity function in the stochastic process. Our empirical results show that our model is able to use samples observed in the lower dimensional space to estimate the higher-order intensity function with extremely sparse observations.

Time-varying neural network for stock return prediction

We consider the problem of neural network training in a time-varying context. Machine learning algorithms have excelled in problems that do not change over time. However, problems encountered in financial markets are often non-stationary. We propose the online early stopping algorithm and show that a neural network trained using this algorithm can track a function changing with unknown dynamics. We applied the proposed algorithm to the stock return prediction problem studied in Gu et al. (2019) and achieved mean rank correlation of 4.69%, almost twice as high as the expanding window approach. We also show that prominent factors, such as the size effect and momentum, exhibit time varying stock return predictiveness.

Novel semi-metrics for multivariate change point analysis and anomaly detection

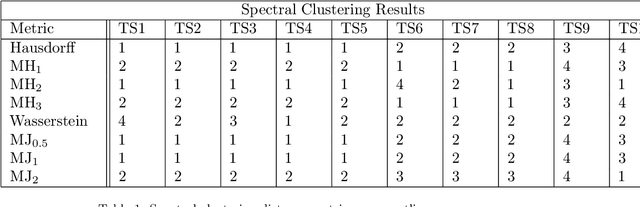
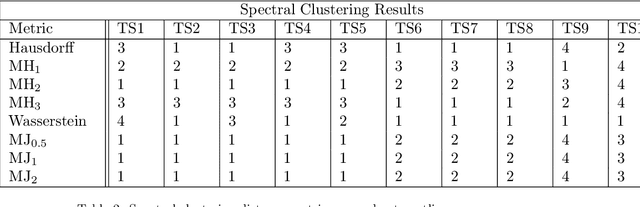
This paper proposes a new method for determining similarity and anomalies between time series, most practically effective in large collections of (likely related) time series, with a particular focus on measuring distances between structural breaks within such a collection. We consolidate and generalise a class of semi-metric distance measures, which we term MJ distances. Experiments on simulated data demonstrate that our proposed family of distances uncover similarity within collections of time series more effectively than measures such as the Hausdorff and Wasserstein metrics. Although our class of distances do not necessarily satisfy the triangle inequality requirement of a metric, we analyse the transitivity properties of respective distance matrices in various contextual scenarios. There, we demonstrate a trade-off between robust performance in the presence of outliers, and the triangle inequality property. We show in experiments using real data that the contrived scenarios that severely violate the transitivity property rarely exhibit themselves in real data; instead, our family of measures satisfies all the properties of a metric most of the time. We illustrate three ways of analysing the distance and similarity matrices, via eigenvalue analysis, hierarchical clustering, and spectral clustering. The results from our hierarchical and spectral clustering experiments on simulated data demonstrate that the Hausdorff and Wasserstein metrics may lead to erroneous inference as to which time series are most similar with respect to their structural breaks, while our semi-metrics provide an improvement.

Hierarchical Probabilistic Model for Blind Source Separation via Legendre Transformation

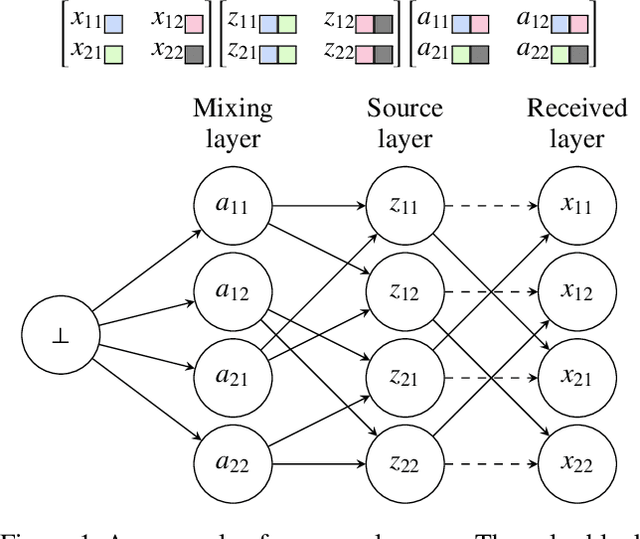
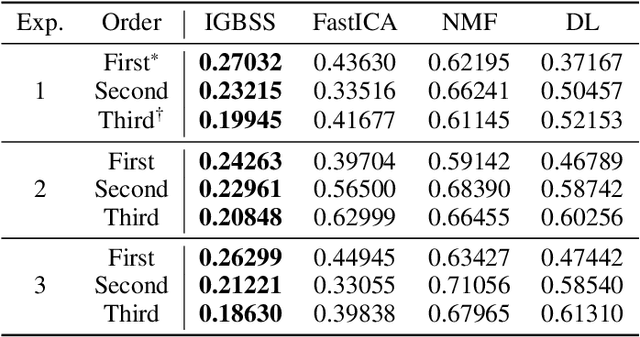
We present a novel blind source separation (BSS) method, called information geometric blind source separation (IGBSS). Our formulation is based on the information geometric log-linear model equipped with a hierarchically structured sample space, which has theoretical guarantees to uniquely recover a set of source signals by minimizing the KL divergence from a set of mixed signals. Source signals, received signals, and mixing matrices are realized as different layers in our hierarchical sample space. Our empirical results have demonstrated on images that our approach is superior to current state-of-the-art techniques and is able to separate signals with complex interactions.