Novel semi-metrics for multivariate change point analysis and anomaly detection

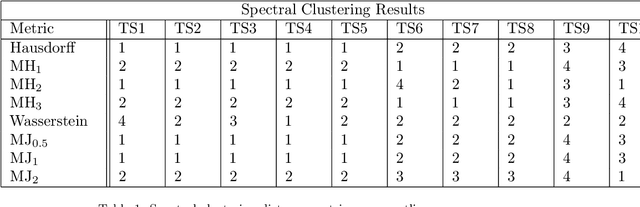
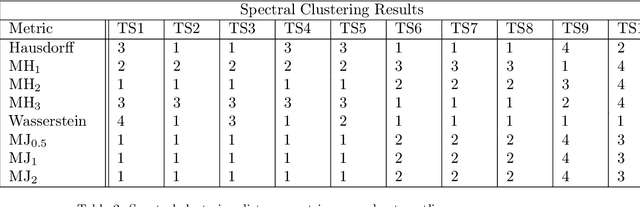
This paper proposes a new method for determining similarity and anomalies between time series, most practically effective in large collections of (likely related) time series, with a particular focus on measuring distances between structural breaks within such a collection. We consolidate and generalise a class of semi-metric distance measures, which we term MJ distances. Experiments on simulated data demonstrate that our proposed family of distances uncover similarity within collections of time series more effectively than measures such as the Hausdorff and Wasserstein metrics. Although our class of distances do not necessarily satisfy the triangle inequality requirement of a metric, we analyse the transitivity properties of respective distance matrices in various contextual scenarios. There, we demonstrate a trade-off between robust performance in the presence of outliers, and the triangle inequality property. We show in experiments using real data that the contrived scenarios that severely violate the transitivity property rarely exhibit themselves in real data; instead, our family of measures satisfies all the properties of a metric most of the time. We illustrate three ways of analysing the distance and similarity matrices, via eigenvalue analysis, hierarchical clustering, and spectral clustering. The results from our hierarchical and spectral clustering experiments on simulated data demonstrate that the Hausdorff and Wasserstein metrics may lead to erroneous inference as to which time series are most similar with respect to their structural breaks, while our semi-metrics provide an improvement.