The Llama 3 Herd of Models

Modern artificial intelligence (AI) systems are powered by foundation models. This paper presents a new set of foundation models, called Llama 3. It is a herd of language models that natively support multilinguality, coding, reasoning, and tool usage. Our largest model is a dense Transformer with 405B parameters and a context window of up to 128K tokens. This paper presents an extensive empirical evaluation of Llama 3. We find that Llama 3 delivers comparable quality to leading language models such as GPT-4 on a plethora of tasks. We publicly release Llama 3, including pre-trained and post-trained versions of the 405B parameter language model and our Llama Guard 3 model for input and output safety. The paper also presents the results of experiments in which we integrate image, video, and speech capabilities into Llama 3 via a compositional approach. We observe this approach performs competitively with the state-of-the-art on image, video, and speech recognition tasks. The resulting models are not yet being broadly released as they are still under development.

Time-varying neural network for stock return prediction

We consider the problem of neural network training in a time-varying context. Machine learning algorithms have excelled in problems that do not change over time. However, problems encountered in financial markets are often non-stationary. We propose the online early stopping algorithm and show that a neural network trained using this algorithm can track a function changing with unknown dynamics. We applied the proposed algorithm to the stock return prediction problem studied in Gu et al. (2019) and achieved mean rank correlation of 4.69%, almost twice as high as the expanding window approach. We also show that prominent factors, such as the size effect and momentum, exhibit time varying stock return predictiveness.

Identifying similarity and anomalies for cryptocurrency moments and distribution extremities

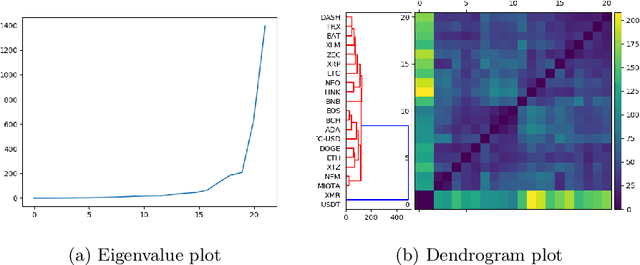
We propose two new methods for identifying similarity and anomalies among collections of time series, and apply these methods to analyse cryptocurrencies. First, we analyse change points with respect to various distribution moments, considering these points as signals of erratic behaviour and potential risk. This technique uses the MJ$_1$ semi-metric, from the more general MJ$_p$ class of semi-metrics \citep{James2019}, to measure distance between these change point sets. Prior work on this topic fails to consider data between change points, and in particular, does not justify the utility of this change point analysis. Therefore, we introduce a second method to determine similarity between time series, in this instance with respect to their extreme values, or tail behaviour. Finally, we measure the consistency between our two methods, that is, structural break versus tail behaviour similarity. With cryptocurrency investment as an apt example of erratic, extreme behaviour, we notice an impressive consistency between these two methods.

Novel semi-metrics for multivariate change point analysis and anomaly detection

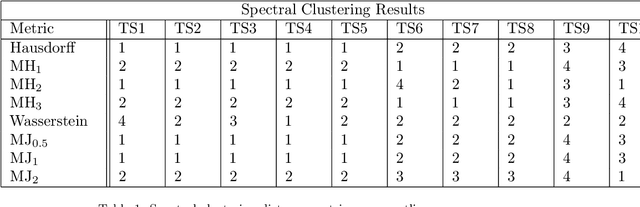
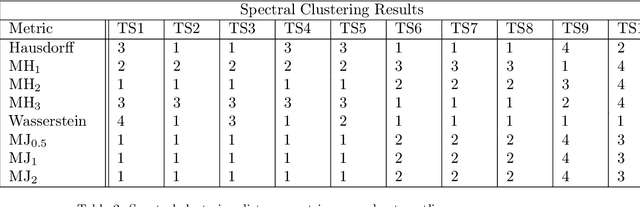
This paper proposes a new method for determining similarity and anomalies between time series, most practically effective in large collections of (likely related) time series, with a particular focus on measuring distances between structural breaks within such a collection. We consolidate and generalise a class of semi-metric distance measures, which we term MJ distances. Experiments on simulated data demonstrate that our proposed family of distances uncover similarity within collections of time series more effectively than measures such as the Hausdorff and Wasserstein metrics. Although our class of distances do not necessarily satisfy the triangle inequality requirement of a metric, we analyse the transitivity properties of respective distance matrices in various contextual scenarios. There, we demonstrate a trade-off between robust performance in the presence of outliers, and the triangle inequality property. We show in experiments using real data that the contrived scenarios that severely violate the transitivity property rarely exhibit themselves in real data; instead, our family of measures satisfies all the properties of a metric most of the time. We illustrate three ways of analysing the distance and similarity matrices, via eigenvalue analysis, hierarchical clustering, and spectral clustering. The results from our hierarchical and spectral clustering experiments on simulated data demonstrate that the Hausdorff and Wasserstein metrics may lead to erroneous inference as to which time series are most similar with respect to their structural breaks, while our semi-metrics provide an improvement.