Clustering volatility regimes for dynamic trading strategies

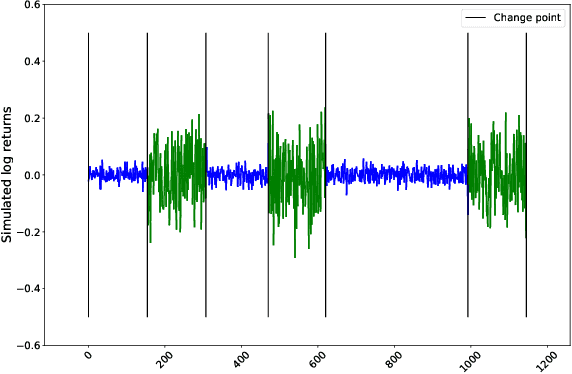
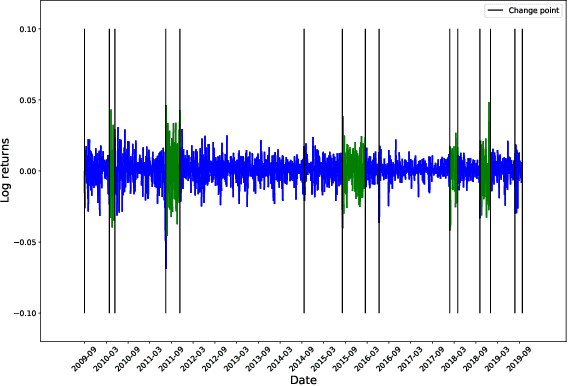
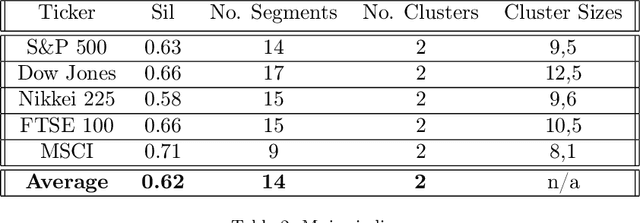
We develop a new method to find the number of volatility regimes in a non-stationary financial time series. We use change point detection to partition a time series into locally stationary segments, then estimate the distributions of each piece. The distributions are clustered into a learned number of discrete volatility regimes via an optimisation routine. Using this method, we investigate and determine a clustering structure for indices, large cap equities and exchange-traded funds. Finally, we create and validate a dynamic portfolio allocation strategy that learns the optimal match between the current distribution of a time series with its past regimes, thereby making online risk-avoidance decisions in the present.

Optimally adaptive Bayesian spectral density estimation

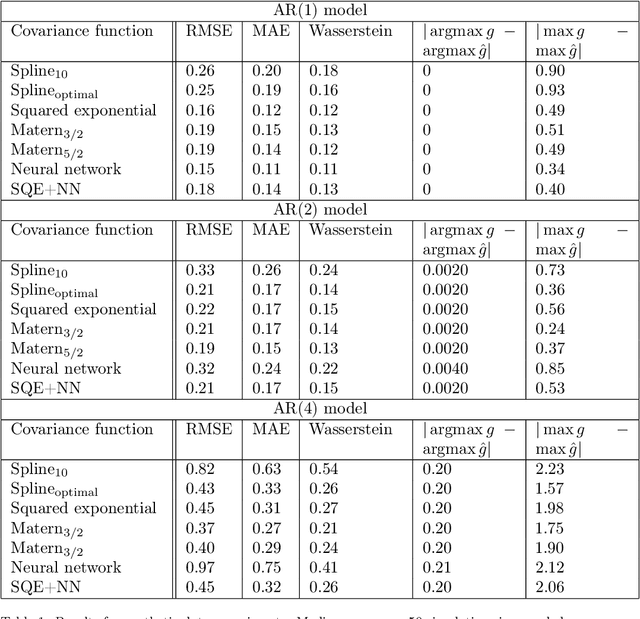
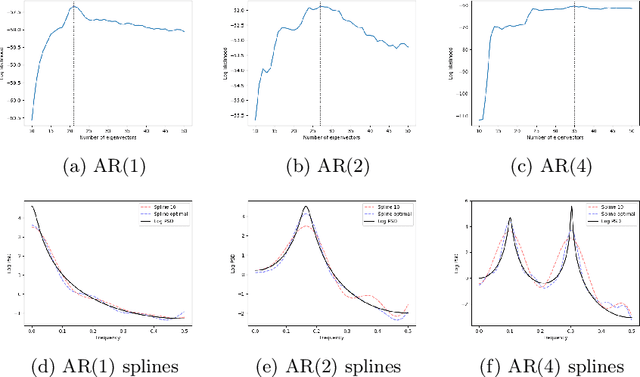
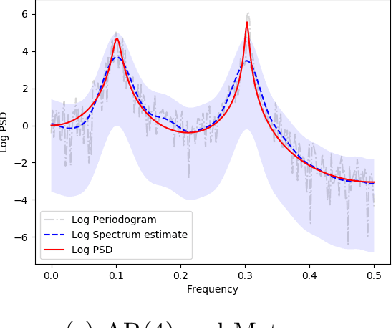
This paper studies spectral density estimates obtained assuming a \emph{Gaussian process} prior, with various stationary and non-stationary covariance structures, modelling the log of the unknown power spectrum. We unify previously disparate techniques from machine learning and statistics, applying various covariance functions to spectral density estimation, and investigate their performance and properties. We show that all covariance functions perform comparatively well, with the smoothing spline model in the existing AdaptSPEC technique performing slightly worse. Subsequently, we propose an improvement on AdaptSPEC based on an optimisation of the number of eigenvectors used. We show this improves on every existing method in the case of stationary time series, and describe an application to non-stationary time series. We introduce new measures of accuracy for the spectral density estimate, inspired from the physical sciences. Finally, we validate our models in an extensive simulation study and with real data, analysing autoregressive processes with known spectra, and sunspot and airline passenger data respectively.

Equivalence relations and $L^p$ distances between time series

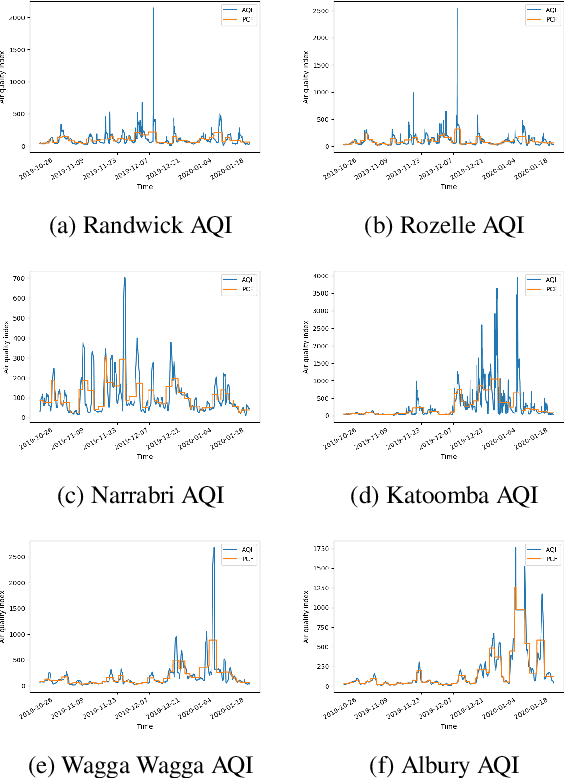
We introduce a general framework for defining equivalence and measuring distances between time series, and a first concrete method for doing so. We prove the existence of equivalence relations on the space of time series, such that the quotient spaces can be equipped with a metrizable topology. We illustrate algorithmically how to calculate such distances among a collection of time series, and perform clustering analysis based on these distances. We apply these insights to analyse the recent bushfires in NSW, Australia. There, we introduce a new method to analyse time series in a cross-contextual setting.

Identifying similarity and anomalies for cryptocurrency moments and distribution extremities

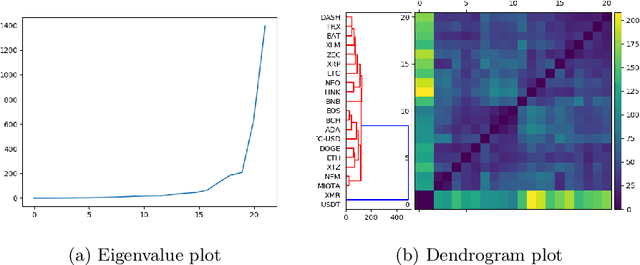
We propose two new methods for identifying similarity and anomalies among collections of time series, and apply these methods to analyse cryptocurrencies. First, we analyse change points with respect to various distribution moments, considering these points as signals of erratic behaviour and potential risk. This technique uses the MJ$_1$ semi-metric, from the more general MJ$_p$ class of semi-metrics \citep{James2019}, to measure distance between these change point sets. Prior work on this topic fails to consider data between change points, and in particular, does not justify the utility of this change point analysis. Therefore, we introduce a second method to determine similarity between time series, in this instance with respect to their extreme values, or tail behaviour. Finally, we measure the consistency between our two methods, that is, structural break versus tail behaviour similarity. With cryptocurrency investment as an apt example of erratic, extreme behaviour, we notice an impressive consistency between these two methods.

Novel semi-metrics for multivariate change point analysis and anomaly detection

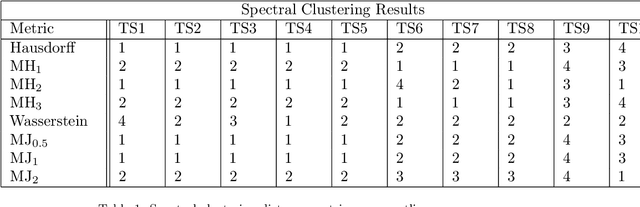
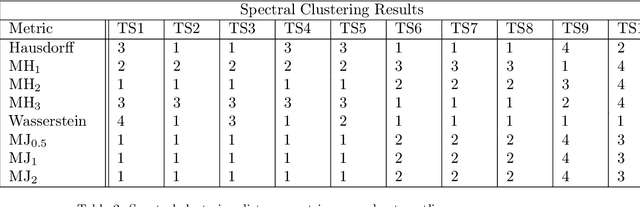
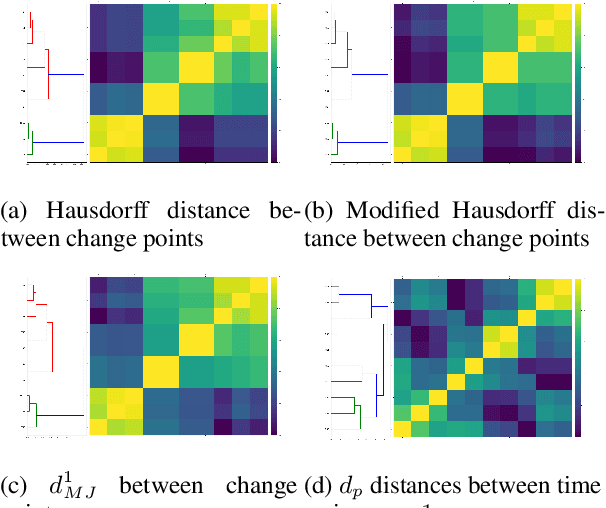
This paper proposes a new method for determining similarity and anomalies between time series, most practically effective in large collections of (likely related) time series, with a particular focus on measuring distances between structural breaks within such a collection. We consolidate and generalise a class of semi-metric distance measures, which we term MJ distances. Experiments on simulated data demonstrate that our proposed family of distances uncover similarity within collections of time series more effectively than measures such as the Hausdorff and Wasserstein metrics. Although our class of distances do not necessarily satisfy the triangle inequality requirement of a metric, we analyse the transitivity properties of respective distance matrices in various contextual scenarios. There, we demonstrate a trade-off between robust performance in the presence of outliers, and the triangle inequality property. We show in experiments using real data that the contrived scenarios that severely violate the transitivity property rarely exhibit themselves in real data; instead, our family of measures satisfies all the properties of a metric most of the time. We illustrate three ways of analysing the distance and similarity matrices, via eigenvalue analysis, hierarchical clustering, and spectral clustering. The results from our hierarchical and spectral clustering experiments on simulated data demonstrate that the Hausdorff and Wasserstein metrics may lead to erroneous inference as to which time series are most similar with respect to their structural breaks, while our semi-metrics provide an improvement.