MANDERA: Malicious Node Detection in Federated Learning via Ranking

Federated learning is a distributed learning paradigm which seeks to preserve the privacy of each participating node's data. However, federated learning is vulnerable to attacks, specifically to our interest, model integrity attacks. In this paper, we propose a novel method for malicious node detection called MANDERA. By transferring the original message matrix into a ranking matrix whose column shows the relative rankings of all local nodes along different parameter dimensions, our approach seeks to distinguish the malicious nodes from the benign ones with high efficiency based on key characteristics of the rank domain. We have proved, under mild conditions, that MANDERA is guaranteed to detect all malicious nodes under typical Byzantine attacks with no prior knowledge or history about the participating nodes. The effectiveness of the proposed approach is further confirmed by experiments on two classic datasets, CIFAR-10 and MNIST. Compared to the state-of-art methods in the literature for defending Byzantine attacks, MANDERA is unique in its way to identify the malicious nodes by ranking and its robustness to effectively defense a wide range of attacks.

Additive Poisson Process: Learning Intensity of Higher-Order Interaction in Stochastic Processes

We present the Additive Poisson Process (APP), a novel framework that can model the higher-order interaction effects of the intensity functions in stochastic processes using lower dimensional projections. Our model combines the techniques in information geometry to model higher-order interactions on a statistical manifold and in generalized additive models to use lower-dimensional projections to overcome the effects from the curse of dimensionality. Our approach solves a convex optimization problem by minimizing the KL divergence from a sample distribution in lower dimensional projections to the distribution modeled by an intensity function in the stochastic process. Our empirical results show that our model is able to use samples observed in the lower dimensional space to estimate the higher-order intensity function with extremely sparse observations.

Semi-supervised Learning Approach to Generate Neuroimaging Modalities with Adversarial Training

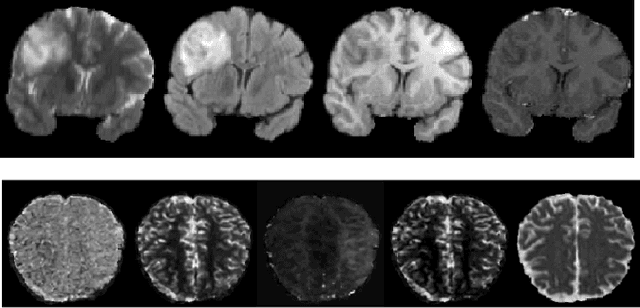
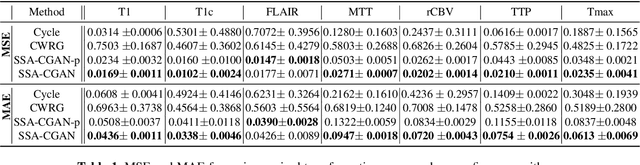
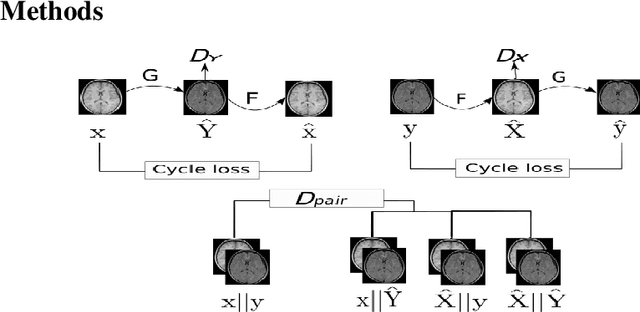
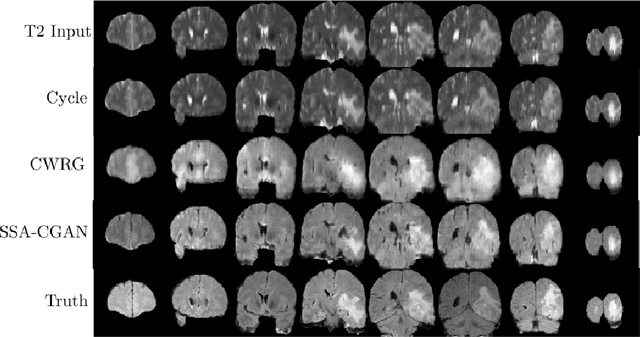
Magnetic Resonance Imaging (MRI) of the brain can come in the form of different modalities such as T1-weighted and Fluid Attenuated Inversion Recovery (FLAIR) which has been used to investigate a wide range of neurological disorders. Current state-of-the-art models for brain tissue segmentation and disease classification require multiple modalities for training and inference. However, the acquisition of all of these modalities are expensive, time-consuming, inconvenient and the required modalities are often not available. As a result, these datasets contain large amounts of \emph{unpaired} data, where examples in the dataset do not contain all modalities. On the other hand, there is smaller fraction of examples that contain all modalities (\emph{paired} data) and furthermore each modality is high dimensional when compared to number of datapoints. In this work, we develop a method to address these issues with semi-supervised learning in translating between two neuroimaging modalities. Our proposed model, Semi-Supervised Adversarial CycleGAN (SSA-CGAN), uses an adversarial loss to learn from \emph{unpaired} data points, cycle loss to enforce consistent reconstructions of the mappings and another adversarial loss to take advantage of \emph{paired} data points. Our experiments demonstrate that our proposed framework produces an improvement in reconstruction error and reduced variance for the pairwise translation of multiple modalities and is more robust to thermal noise when compared to existing methods.

Hierarchical Probabilistic Model for Blind Source Separation via Legendre Transformation

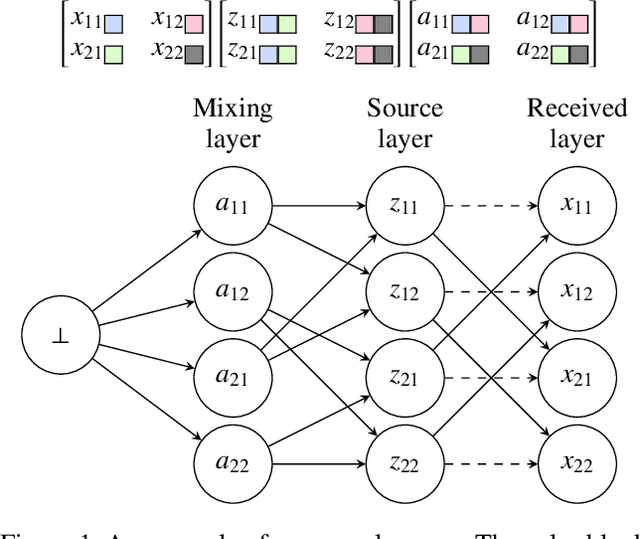
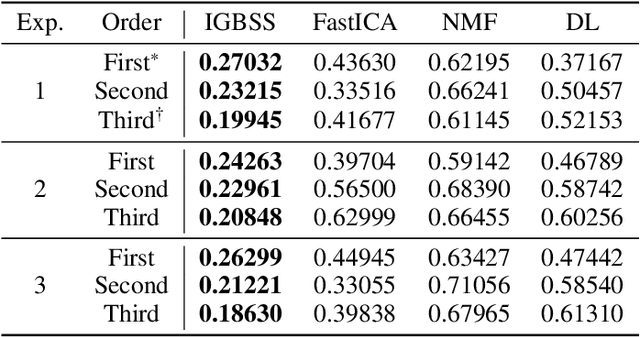
We present a novel blind source separation (BSS) method, called information geometric blind source separation (IGBSS). Our formulation is based on the information geometric log-linear model equipped with a hierarchically structured sample space, which has theoretical guarantees to uniquely recover a set of source signals by minimizing the KL divergence from a set of mixed signals. Source signals, received signals, and mixing matrices are realized as different layers in our hierarchical sample space. Our empirical results have demonstrated on images that our approach is superior to current state-of-the-art techniques and is able to separate signals with complex interactions.

Bias-Variance Trade-Off in Hierarchical Probabilistic Models Using Higher-Order Feature Interactions

Hierarchical probabilistic models are able to use a large number of parameters to create a model with a high representation power. However, it is well known that increasing the number of parameters also increases the complexity of the model which leads to a bias-variance trade-off. Although it is a classical problem, the bias-variance trade-off between hidden layers and higher-order interactions have not been well studied. In our study, we propose an efficient inference algorithm for the log-linear formulation of the higher-order Boltzmann machine using a combination of Gibbs sampling and annealed importance sampling. We then perform a bias-variance decomposition to study the differences in hidden layers and higher-order interactions. Our results have shown that using hidden layers and higher-order interactions have a comparable error with a similar order of magnitude and using higher-order interactions produce less variance for smaller sample size.