Quantifying the Dissimilarity of Texts

Quantifying the dissimilarity of two texts is an important aspect of a number of natural language processing tasks, including semantic information retrieval, topic classification, and document clustering. In this paper, we compared the properties and performance of different dissimilarity measures $D$ using three different representations of texts -- vocabularies, word frequency distributions, and vector embeddings -- and three simple tasks -- clustering texts by author, subject, and time period. Using the Project Gutenberg database, we found that the generalised Jensen--Shannon divergence applied to word frequencies performed strongly across all tasks, that $D$'s based on vector embedding representations led to stronger performance for smaller texts, and that the optimal choice of approach was ultimately task-dependent. We also investigated, both analytically and numerically, the behaviour of the different $D$'s when the two texts varied in length by a factor $h$. We demonstrated that the (natural) estimator of the Jaccard distance between vocabularies was inconsistent and computed explicitly the $h$-dependency of the bias of the estimator of the generalised Jensen--Shannon divergence applied to word frequencies. We also found numerically that the Jensen--Shannon divergence and embedding-based approaches were robust to changes in $h$, while the Jaccard distance was not.

Multilayer Networks for Text Analysis with Multiple Data Types

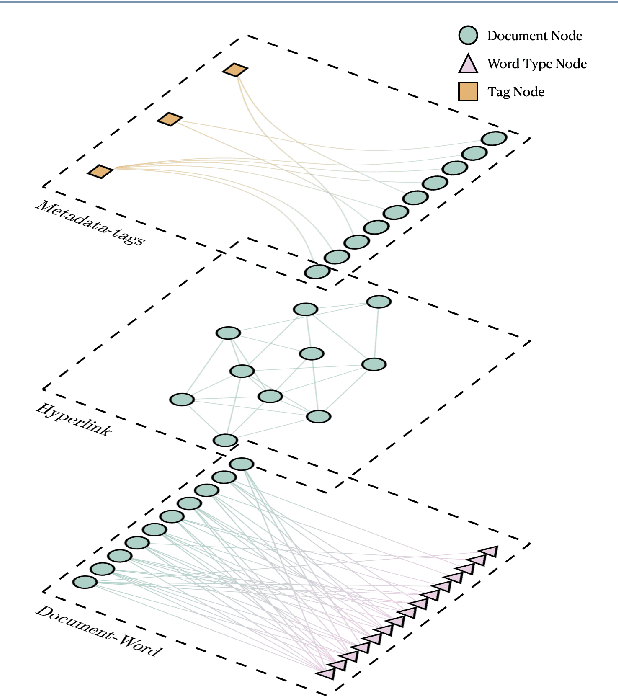
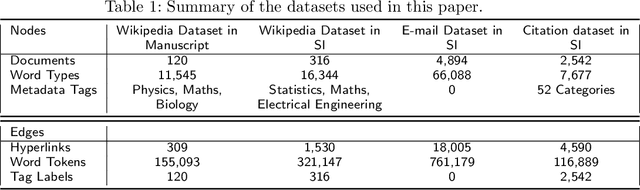
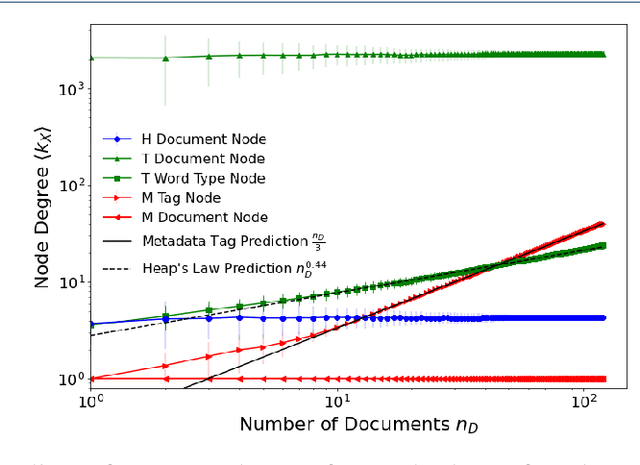
We are interested in the widespread problem of clustering documents and finding topics in large collections of written documents in the presence of metadata and hyperlinks. To tackle the challenge of accounting for these different types of datasets, we propose a novel framework based on Multilayer Networks and Stochastic Block Models. The main innovation of our approach over other techniques is that it applies the same non-parametric probabilistic framework to the different sources of datasets simultaneously. The key difference to other multilayer complex networks is the strong unbalance between the layers, with the average degree of different node types scaling differently with system size. We show that the latter observation is due to generic properties of text, such as Heaps' law, and strongly affects the inference of communities. We present and discuss the performance of our method in different datasets (hundreds of Wikipedia documents, thousands of scientific papers, and thousands of E-mails) showing that taking into account multiple types of information provides a more nuanced view on topic- and document-clusters and increases the ability to predict missing links.

A network approach to topic models

One of the main computational and scientific challenges in the modern age is to extract useful information from unstructured texts. Topic models are one popular machine-learning approach which infers the latent topical structure of a collection of documents. Despite their success --- in particular of its most widely used variant called Latent Dirichlet Allocation (LDA) --- and numerous applications in sociology, history, and linguistics, topic models are known to suffer from severe conceptual and practical problems, e.g. a lack of justification for the Bayesian priors, discrepancies with statistical properties of real texts, and the inability to properly choose the number of topics. Here we obtain a fresh view on the problem of identifying topical structures by relating it to the problem of finding communities in complex networks. This is achieved by representing text corpora as bipartite networks of documents and words. By adapting existing community-detection methods -- using a stochastic block model (SBM) with non-parametric priors -- we obtain a more versatile and principled framework for topic modeling (e.g., it automatically detects the number of topics and hierarchically clusters both the words and documents). The analysis of artificial and real corpora demonstrates that our SBM approach leads to better topic models than LDA in terms of statistical model selection. More importantly, our work shows how to formally relate methods from community detection and topic modeling, opening the possibility of cross-fertilization between these two fields.

Generalized Entropies and the Similarity of Texts

We show how generalized Gibbs-Shannon entropies can provide new insights on the statistical properties of texts. The universal distribution of word frequencies (Zipf's law) implies that the generalized entropies, computed at the word level, are dominated by words in a specific range of frequencies. Here we show that this is the case not only for the generalized entropies but also for the generalized (Jensen-Shannon) divergences, used to compute the similarity between different texts. This finding allows us to identify the contribution of specific words (and word frequencies) for the different generalized entropies and also to estimate the size of the databases needed to obtain a reliable estimation of the divergences. We test our results in large databases of books (from the Google n-gram database) and scientific papers (indexed by Web of Science).

Similarity of symbol frequency distributions with heavy tails

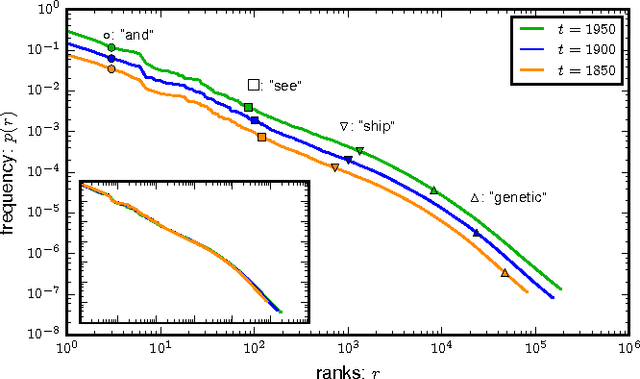
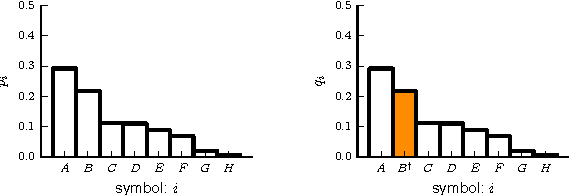
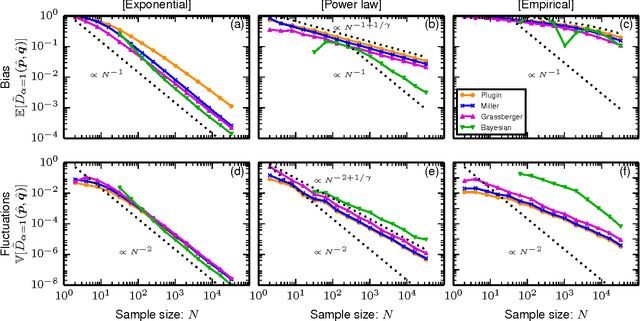
Quantifying the similarity between symbolic sequences is a traditional problem in Information Theory which requires comparing the frequencies of symbols in different sequences. In numerous modern applications, ranging from DNA over music to texts, the distribution of symbol frequencies is characterized by heavy-tailed distributions (e.g., Zipf's law). The large number of low-frequency symbols in these distributions poses major difficulties to the estimation of the similarity between sequences, e.g., they hinder an accurate finite-size estimation of entropies. Here we show analytically how the systematic (bias) and statistical (fluctuations) errors in these estimations depend on the sample size~$N$ and on the exponent~$\gamma$ of the heavy-tailed distribution. Our results are valid for the Shannon entropy $(\alpha=1)$, its corresponding similarity measures (e.g., the Jensen-Shanon divergence), and also for measures based on the generalized entropy of order $\alpha$. For small $\alpha$'s, including $\alpha=1$, the errors decay slower than the $1/N$-decay observed in short-tailed distributions. For $\alpha$ larger than a critical value $\alpha^* = 1+1/\gamma \leq 2$, the $1/N$-decay is recovered. We show the practical significance of our results by quantifying the evolution of the English language over the last two centuries using a complete $\alpha$-spectrum of measures. We find that frequent words change more slowly than less frequent words and that $\alpha=2$ provides the most robust measure to quantify language change.

Statistical laws in linguistics

Zipf's law is just one out of many universal laws proposed to describe statistical regularities in language. Here we review and critically discuss how these laws can be statistically interpreted, fitted, and tested (falsified). The modern availability of large databases of written text allows for tests with an unprecedent statistical accuracy and also a characterization of the fluctuations around the typical behavior. We find that fluctuations are usually much larger than expected based on simplifying statistical assumptions (e.g., independence and lack of correlations between observations).These simplifications appear also in usual statistical tests so that the large fluctuations can be erroneously interpreted as a falsification of the law. Instead, here we argue that linguistic laws are only meaningful (falsifiable) if accompanied by a model for which the fluctuations can be computed (e.g., a generative model of the text). The large fluctuations we report show that the constraints imposed by linguistic laws on the creativity process of text generation are not as tight as one could expect.

Scaling laws and fluctuations in the statistics of word frequencies

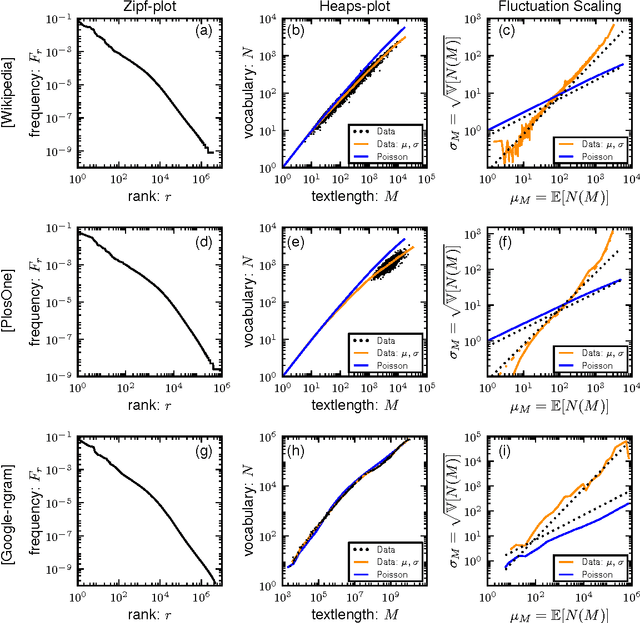
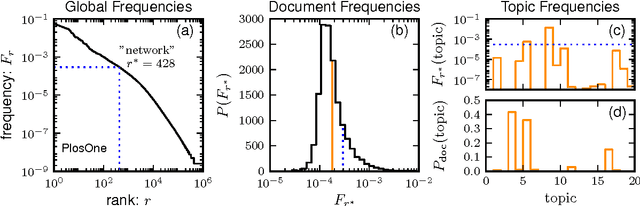
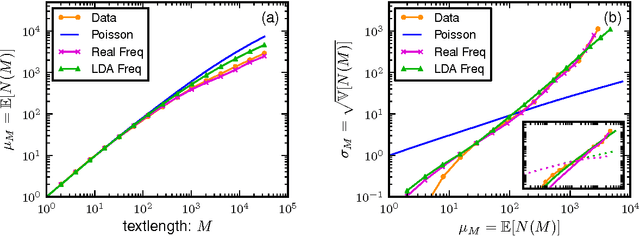
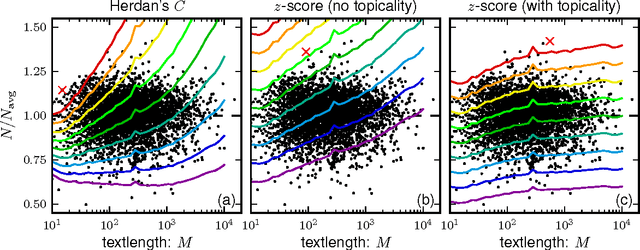
In this paper we combine statistical analysis of large text databases and simple stochastic models to explain the appearance of scaling laws in the statistics of word frequencies. Besides the sublinear scaling of the vocabulary size with database size (Heaps' law), here we report a new scaling of the fluctuations around this average (fluctuation scaling analysis). We explain both scaling laws by modeling the usage of words by simple stochastic processes in which the overall distribution of word-frequencies is fat tailed (Zipf's law) and the frequency of a single word is subject to fluctuations across documents (as in topic models). In this framework, the mean and the variance of the vocabulary size can be expressed as quenched averages, implying that: i) the inhomogeneous dissemination of words cause a reduction of the average vocabulary size in comparison to the homogeneous case, and ii) correlations in the co-occurrence of words lead to an increase in the variance and the vocabulary size becomes a non-self-averaging quantity. We address the implications of these observations to the measurement of lexical richness. We test our results in three large text databases (Google-ngram, Enlgish Wikipedia, and a collection of scientific articles).

Extracting information from S-curves of language change

It is well accepted that adoption of innovations are described by S-curves (slow start, accelerating period, and slow end). In this paper, we analyze how much information on the dynamics of innovation spreading can be obtained from a quantitative description of S-curves. We focus on the adoption of linguistic innovations for which detailed databases of written texts from the last 200 years allow for an unprecedented statistical precision. Combining data analysis with simulations of simple models (e.g., the Bass dynamics on complex networks) we identify signatures of endogenous and exogenous factors in the S-curves of adoption. We propose a measure to quantify the strength of these factors and three different methods to estimate it from S-curves. We obtain cases in which the exogenous factors are dominant (in the adoption of German orthographic reforms and of one irregular verb) and cases in which endogenous factors are dominant (in the adoption of conventions for romanization of Russian names and in the regularization of most studied verbs). These results show that the shape of S-curve is not universal and contains information on the adoption mechanism. (published at "J. R. Soc. Interface, vol. 11, no. 101, (2014) 1044"; DOI: http://dx.doi.org/10.1098/rsif.2014.1044)

Stochastic model for the vocabulary growth in natural languages

We propose a stochastic model for the number of different words in a given database which incorporates the dependence on the database size and historical changes. The main feature of our model is the existence of two different classes of words: (i) a finite number of core-words which have higher frequency and do not affect the probability of a new word to be used; and (ii) the remaining virtually infinite number of noncore-words which have lower frequency and once used reduce the probability of a new word to be used in the future. Our model relies on a careful analysis of the google-ngram database of books published in the last centuries and its main consequence is the generalization of Zipf's and Heaps' law to two scaling regimes. We confirm that these generalizations yield the best simple description of the data among generic descriptive models and that the two free parameters depend only on the language but not on the database. From the point of view of our model the main change on historical time scales is the composition of the specific words included in the finite list of core-words, which we observe to decay exponentially in time with a rate of approximately 30 words per year for English.

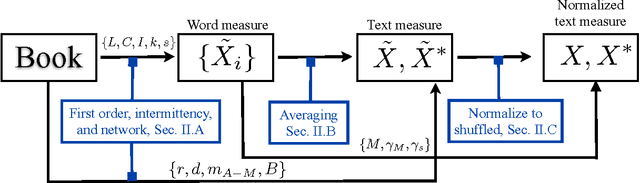
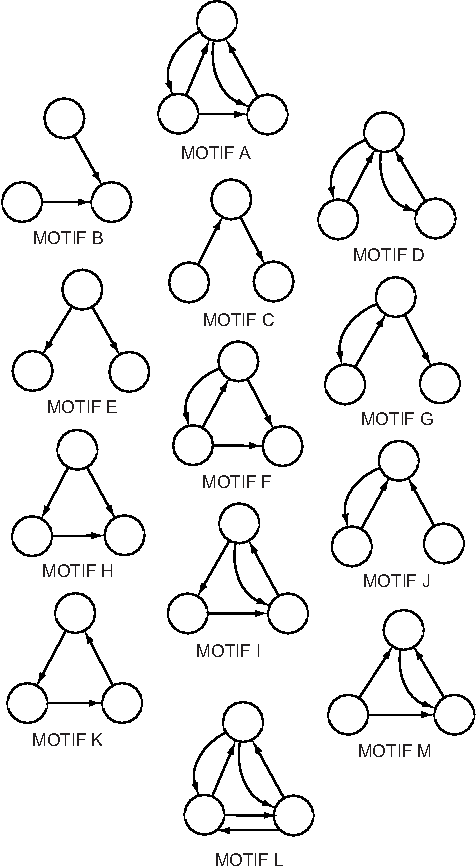
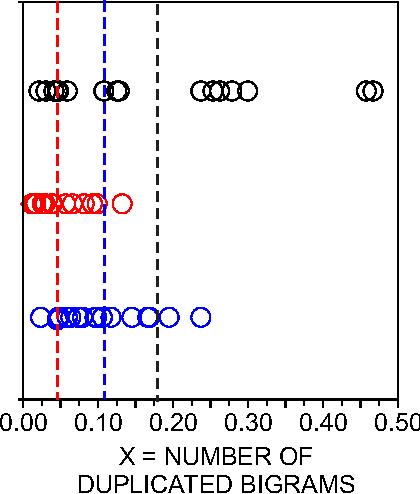
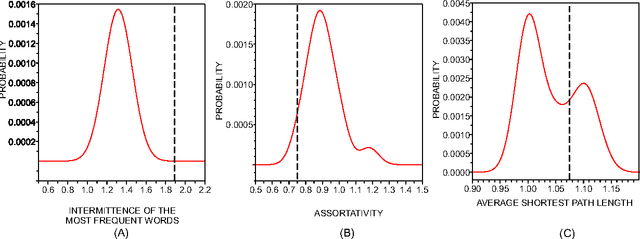
Probing the statistical properties of unknown texts: application to the Voynich Manuscript

While the use of statistical physics methods to analyze large corpora has been useful to unveil many patterns in texts, no comprehensive investigation has been performed investigating the properties of statistical measurements across different languages and texts. In this study we propose a framework that aims at determining if a text is compatible with a natural language and which languages are closest to it, without any knowledge of the meaning of the words. The approach is based on three types of statistical measurements, i.e. obtained from first-order statistics of word properties in a text, from the topology of complex networks representing text, and from intermittency concepts where text is treated as a time series. Comparative experiments were performed with the New Testament in 15 different languages and with distinct books in English and Portuguese in order to quantify the dependency of the different measurements on the language and on the story being told in the book. The metrics found to be informative in distinguishing real texts from their shuffled versions include assortativity, degree and selectivity of words. As an illustration, we analyze an undeciphered medieval manuscript known as the Voynich Manuscript. We show that it is mostly compatible with natural languages and incompatible with random texts. We also obtain candidates for key-words of the Voynich Manuscript which could be helpful in the effort of deciphering it. Because we were able to identify statistical measurements that are more dependent on the syntax than on the semantics, the framework may also serve for text analysis in language-dependent applications.