A standardized Project Gutenberg corpus for statistical analysis of natural language and quantitative linguistics

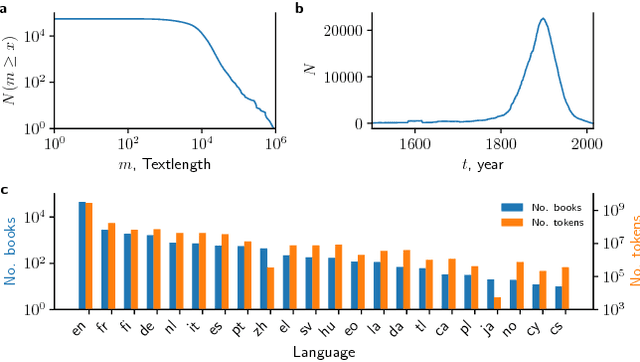
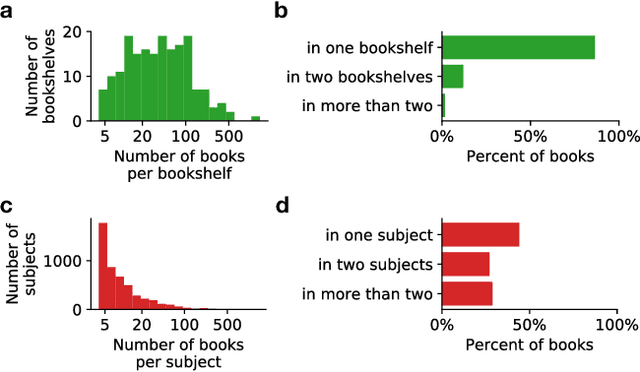
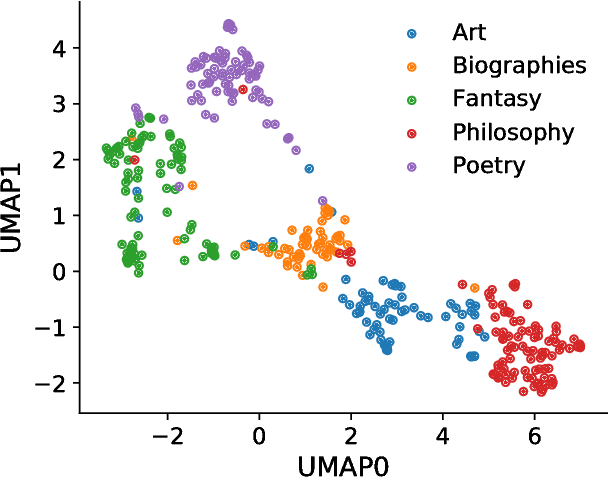
The use of Project Gutenberg (PG) as a text corpus has been extremely popular in statistical analysis of language for more than 25 years. However, in contrast to other major linguistic datasets of similar importance, no consensual full version of PG exists to date. In fact, most PG studies so far either consider only a small number of manually selected books, leading to potential biased subsets, or employ vastly different pre-processing strategies (often specified in insufficient details), raising concerns regarding the reproducibility of published results. In order to address these shortcomings, here we present the Standardized Project Gutenberg Corpus (SPGC), an open science approach to a curated version of the complete PG data containing more than 50,000 books and more than $3 \times 10^9$ word-tokens. Using different sources of annotated metadata, we not only provide a broad characterization of the content of PG, but also show different examples highlighting the potential of SPGC for investigating language variability across time, subjects, and authors. We publish our methodology in detail, the code to download and process the data, as well as the obtained corpus itself on 3 different levels of granularity (raw text, timeseries of word tokens, and counts of words). In this way, we provide a reproducible, pre-processed, full-size version of Project Gutenberg as a new scientific resource for corpus linguistics, natural language processing, and information retrieval.

Similarity of symbol frequency distributions with heavy tails

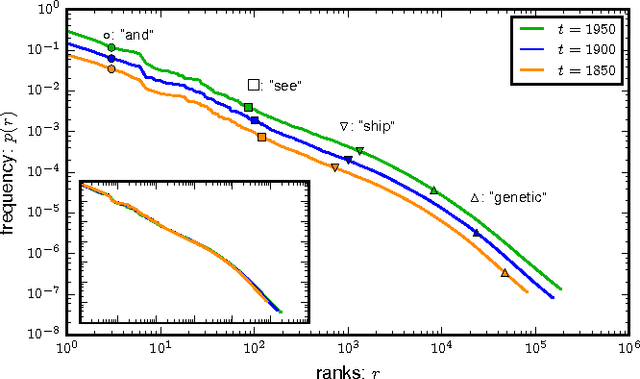
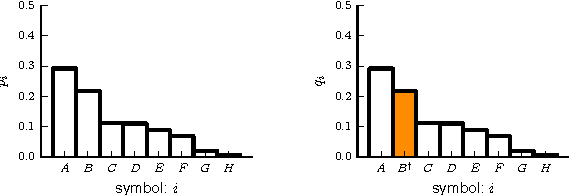
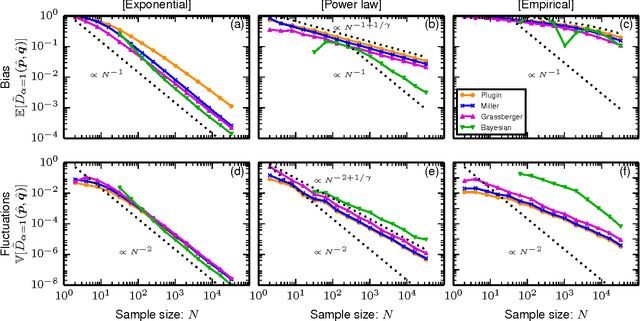
Quantifying the similarity between symbolic sequences is a traditional problem in Information Theory which requires comparing the frequencies of symbols in different sequences. In numerous modern applications, ranging from DNA over music to texts, the distribution of symbol frequencies is characterized by heavy-tailed distributions (e.g., Zipf's law). The large number of low-frequency symbols in these distributions poses major difficulties to the estimation of the similarity between sequences, e.g., they hinder an accurate finite-size estimation of entropies. Here we show analytically how the systematic (bias) and statistical (fluctuations) errors in these estimations depend on the sample size~$N$ and on the exponent~$\gamma$ of the heavy-tailed distribution. Our results are valid for the Shannon entropy $(\alpha=1)$, its corresponding similarity measures (e.g., the Jensen-Shanon divergence), and also for measures based on the generalized entropy of order $\alpha$. For small $\alpha$'s, including $\alpha=1$, the errors decay slower than the $1/N$-decay observed in short-tailed distributions. For $\alpha$ larger than a critical value $\alpha^* = 1+1/\gamma \leq 2$, the $1/N$-decay is recovered. We show the practical significance of our results by quantifying the evolution of the English language over the last two centuries using a complete $\alpha$-spectrum of measures. We find that frequent words change more slowly than less frequent words and that $\alpha=2$ provides the most robust measure to quantify language change.