Scaling laws and fluctuations in the statistics of word frequencies

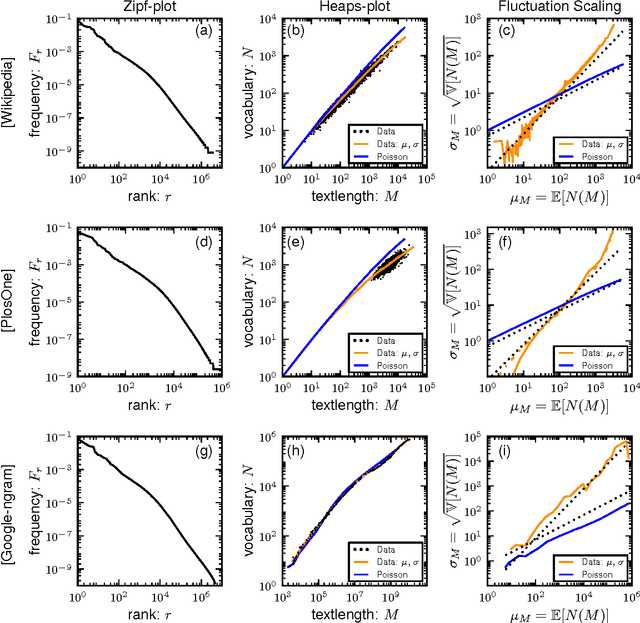
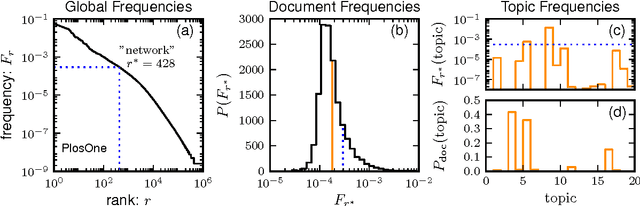
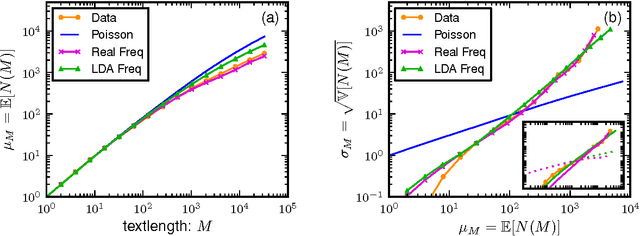
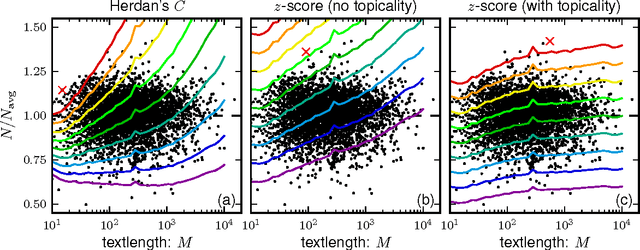
In this paper we combine statistical analysis of large text databases and simple stochastic models to explain the appearance of scaling laws in the statistics of word frequencies. Besides the sublinear scaling of the vocabulary size with database size (Heaps' law), here we report a new scaling of the fluctuations around this average (fluctuation scaling analysis). We explain both scaling laws by modeling the usage of words by simple stochastic processes in which the overall distribution of word-frequencies is fat tailed (Zipf's law) and the frequency of a single word is subject to fluctuations across documents (as in topic models). In this framework, the mean and the variance of the vocabulary size can be expressed as quenched averages, implying that: i) the inhomogeneous dissemination of words cause a reduction of the average vocabulary size in comparison to the homogeneous case, and ii) correlations in the co-occurrence of words lead to an increase in the variance and the vocabulary size becomes a non-self-averaging quantity. We address the implications of these observations to the measurement of lexical richness. We test our results in three large text databases (Google-ngram, Enlgish Wikipedia, and a collection of scientific articles).