Normalization in Proportional Feature Spaces

The subject of features normalization plays an important central role in data representation, characterization, visualization, analysis, comparison, classification, and modeling, as it can substantially influence and be influenced by all of these activities and respective aspects. The selection of an appropriate normalization method needs to take into account the type and characteristics of the involved features, the methods to be used subsequently for the just mentioned data processing, as well as the specific questions being considered. After briefly considering how normalization constitutes one of the many interrelated parts typically involved in data analysis and modeling, the present work addressed the important issue of feature normalization from the perspective of uniform and proportional (right skewed) features and comparison operations. More general right skewed features are also considered in an approximated manner. Several concepts, properties, and results are described and discussed, including the description of a duality relationship between uniform and proportional feature spaces and respective comparisons, specifying conditions for consistency between comparisons in each of the two domains. Two normalization possibilities based on non-centralized dispersion of features are also presented, and also described is a modified version of the Jaccard similarity index which incorporates intrinsically normalization. Preliminary experiments are presented in order to illustrate the developed concepts and methods.

Supervised Pattern Recognition Involving Skewed Feature Densities

Pattern recognition constitutes a particularly important task underlying a great deal of scientific and technologica activities. At the same time, pattern recognition involves several challenges, including the choice of features to represent the data elements, as well as possible respective transformations. In the present work, the classification potential of the Euclidean distance and a dissimilarity index based on the coincidence similarity index are compared by using the k-neighbors supervised classification method respectively to features resulting from several types of transformations of one- and two-dimensional symmetric densities. Given two groups characterized by respective densities without or with overlap, different types of respective transformations are obtained and employed to quantitatively evaluate the performance of k-neighbors methodologies based on the Euclidean distance an coincidence similarity index. More specifically, the accuracy of classifying the intersection point between the densities of two adjacent groups is taken into account for the comparison. Several interesting results are described and discussed, including the enhanced potential of the dissimilarity index for classifying datasets with right skewed feature densities, as well as the identification that the sharpness of the comparison between data elements can be independent of the respective supervised classification performance.

Two Approaches to Supervised Image Segmentation

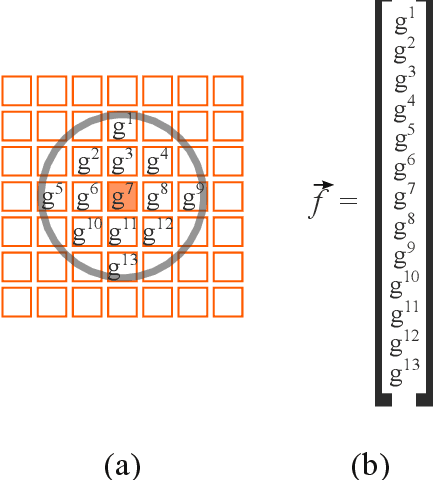
Though performed almost effortlessly by humans, segmenting 2D gray-scale or color images in terms of regions of interest (e.g.~background, objects, or portions of objects) constitutes one of the greatest challenges in science and technology as a consequence of the involved dimensionality reduction(3D to 2D), noise, reflections, shades, and occlusions, among many other possible effects. While a large number of interesting related approaches have been suggested along the last decades, it was mainly thanks to the recent development of deep learning that more effective and general solutions have been obtained, currently constituting the basic comparison reference for this type of operation. Also developed recently, a multiset-based methodology has been described that is capable of encouraging image segmentation performance while combining spatial accuracy, stability, and robustness while requiring little computational resources (hardware and/or training and recognition time). The interesting features of the multiset neurons methodology mostly follow from the enhanced selectivity and sensitivity, as well as good robustness to data perturbations and outliers, allowed by the coincidence similarity index on which the multiset approach to supervised image segmentation is based. After describing the deep learning and multiset neurons approaches, the present work develops two comparison experiments between them which are primarily aimed at illustrating their respective main interesting features when applied to the adopted specific type of data and parameter configurations. While the deep learning approach confirmed its potential for performing image segmentation, the alternative multiset methodology allowed for enhanced accuracy while requiring little computational resources.

Using Full-Text Content to Characterize and Identify Best Seller Books

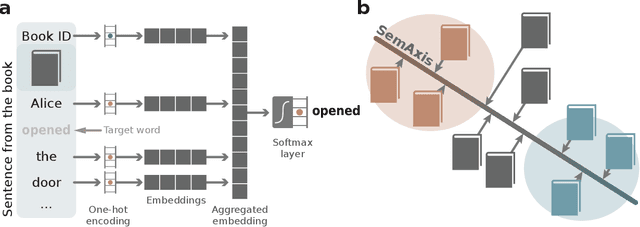
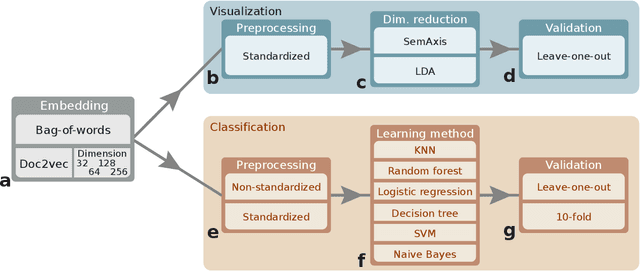
Artistic pieces can be studied from several perspectives, one example being their reception among readers over time. In the present work, we approach this interesting topic from the standpoint of literary works, particularly assessing the task of predicting whether a book will become a best seller. Dissimilarly from previous approaches, we focused on the full content of books and considered visualization and classification tasks. We employed visualization for the preliminary exploration of the data structure and properties, involving SemAxis and linear discriminant analyses. Then, to obtain quantitative and more objective results, we employed various classifiers. Such approaches were used along with a dataset containing (i) books published from 1895 to 1924 and consecrated as best sellers by the \emph{Publishers Weekly Bestseller Lists} and (ii) literary works published in the same period but not being mentioned in that list. Our comparison of methods revealed that the best-achieved result - combining a bag-of-words representation with a logistic regression classifier - led to an average accuracy of 0.75 both for the leave-one-out and 10-fold cross-validations. Such an outcome suggests that it is unfeasible to predict the success of books with high accuracy using only the full content of the texts. Nevertheless, our findings provide insights into the factors leading to the relative success of a literary work.

Accessibility and Trajectory-Based Text Characterization

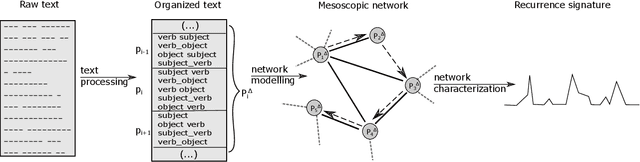
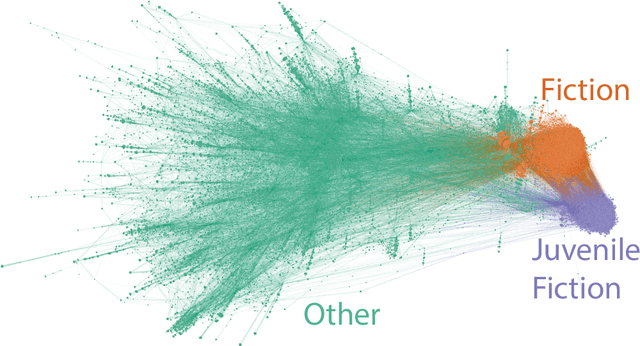
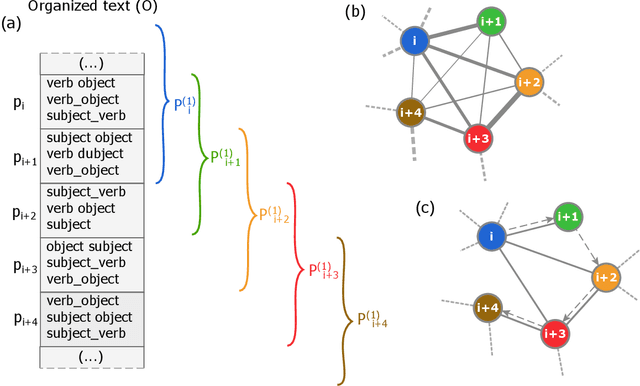
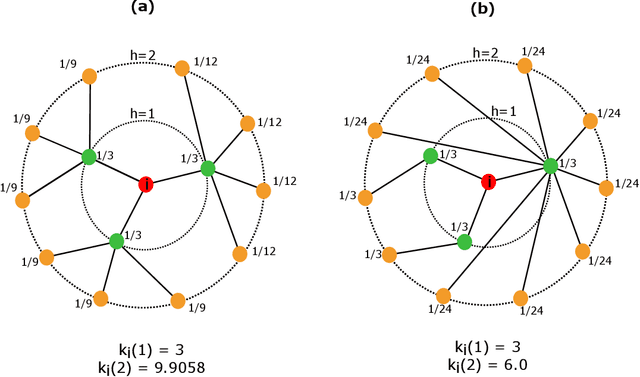
Several complex systems are characterized by presenting intricate characteristics extending along many scales. These characterizations are used in various applications, including text classification, better understanding of diseases, and comparison between cities, among others. In particular, texts are also characterized by a hierarchical structure that can be approached by using multi-scale concepts and methods. The present work aims at developing these possibilities while focusing on mesoscopic representations of networks. More specifically, we adopt an extension to the mesoscopic approach to represent text narratives, in which only the recurrent relationships among tagged parts of speech are considered to establish connections among sequential pieces of text (e.g., paragraphs). The characterization of the texts was then achieved by considering scale-dependent complementary methods: accessibility, symmetry and recurrence signatures. In order to evaluate the potential of these concepts and methods, we approached the problem of distinguishing between literary genres (fiction and non-fiction). A set of 300 books organized into the two genres was considered and were compared by using the aforementioned approaches. All the methods were capable of differentiating to some extent between the two genres. The accessibility and symmetry reflected the narrative asymmetries, while the recurrence signature provide a more direct indication about the non-sequential semantic connections taking place along the narrative.

Comparing Cross Correlation-Based Similarities

The real-valued Jaccard and coincidence indices, in addition to their conceptual and computational simplicity, have been verified to be able to provide promising results in tasks such as template matching, tending to yield peaks that are sharper and narrower than those typically obtained by standard cross-correlation, while also attenuating substantially secondary matchings. In this work, the multiset-based correlations based on the real-valued multiset Jaccard and coincidence indices are compared from the perspective of template matching, with encouraging results which have implications for pattern recognition, deep learning, and scientific modeling in general. The multiset-based correlation methods, and especially the coincidence index, presented remarkable performance characterized by sharper and narrower peaks while secondary peaks were attenuated, which was maintained even in presence of intense levels of noise. In particular, the two methods derived from the coincidence index led to particularly interesting results. The cross correlation, however, presented the best robustness to symmetric additive noise, which suggested a new combination of the considered approaches. After a preliminary investigation of the relative performance of the multiset approaches, as well as the classic cross-correlation, a systematic comparison framework is proposed and applied for the study of the aforementioned methods. Several results are reported, including the confirmation, at least for the considered type of data, of the coincidence correlation as providing enhanced performance regarding detection of narrow, sharp peaks while secondary matches are duly attenuated. The combined method also resulted promising for dealing with signals in presence of intense additive noise.

Multiset Signal Processing and Electronics

Multisets are an intuitive extension of the traditional concept of sets that allow repetition of elements, with the number of times each element appears being understood as the respective multiplicity. Recent generalizations of multisets to real-valued functions, accounting for possibly negative values, have paved the way to a number of interesting implications and applications, including respective implementations as electronic systems. The basic multiset operations include the set complementation (sign change), intersection (minimum between two values), union (maximum between two values), difference and sum (identical to the algebraic counterparts). When applied to functions or signals, the sign and conjoint sign functions are also required. Given that signals are functions, it becomes possible to effectively translate the multiset and multifunction operations to analog electronics, which is the objective of the present work. It is proposed that effective multiset operations capable of high performance self and cross-correlation can be obtained with relative simplicity in either discrete or integrated circuits. The problem of switching noise is also briefly discussed. The present results have great potential for applications and related developments in analog and digital electronics, as well as for pattern recognition, signal processing, and deep learning.

Common Product Neurons

The present work develops a comparative performance of artificial neurons obtained in terms of the recently introduced real-valued Jaccard and coincidence indices and respective functionals. The interiority index and classic cross-correlation are also included in our study. After presenting the basic concepts related to multisets and the adopted similarity metrics, including new results about the generalization of the family of real-valued Jaccard and conicidence indices to higher orders, we proceed to studying the response of a single neuron, not taking into account the output non-linearity (e.g.~sigmoid), respectively to the detection of a gaussian stimulus in presence of displacement, magnification, intensity variation, noise and interference from additional patterns. It is shown that the real-valued Jaccard and coincidence approaches are substantially more robust and effective than the interiority index and the classic cross-correlation. The coincidence based neurons are shown to have the best overall performance for the considered type of data and perturbations. The reported concepts, methods, and results, have substantial implications not only for patter recognition and deep learning, but also regarding neurobiology and neuroscience.

On Similarity

The objective quantification of similarity between two mathematical structures constitutes a recurrent issue in science and technology. In the present work, we developed a principled approach that took the Kronecker's delta function of two scalar values as the prototypical reference for similarity quantification and then derived for more yielding indices, three of which bound between 0 and 1. Generalizations of these indices to take into account the sign of the scalar values were then presented and developed to multisets, vectors, and functions in real spaces. Several important results have been obtained, including the interpretation of the Jaccard index as a yielding implementation of the Kronecker's delta function. When generalized to real functions, the four described similarity indices become respective functionals, which can then be employed to obtain associated operations of convolution and correlation.

Further Generalizations of the Jaccard Index

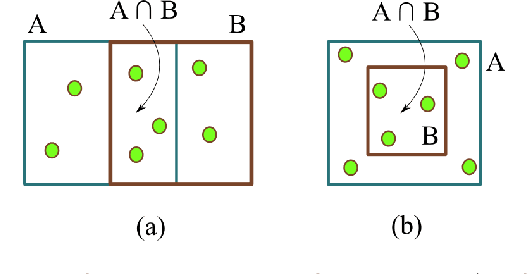
Quantifying the similarity between two sets constitutes a particularly interesting and useful operation in several theoretical and applied problems involving set theory. Aimed at quantifying the similarity between two sets, the Jaccard index has been extensively used in the most diverse types of problems, also motivating respective generalizations. The present work addressew further generalizations of this index, including its modification into a coincidence index capable of accounting also for the level of interiority of the sets, an extension for sets in continuous vector spaces, the consideration of weights associated to the involved set elements, the generalization to multiset addition, densities and generic scalar fields, as well as a means to quantify the joint interdependence between random variables. The also interesting possibility to take into account more than two sets was also addressed, including the description of an index capable of quantifying the level of chaining between three sets. Several of the described and suggested generalizations have been illustrated with respect to numeric case examples. It is also posited that these indices can play an important role while analyzing and integrating datasets in modeling approaches and pattern recognition activities.