Alexandre Benatti
Normalization in Proportional Feature Spaces
Sep 17, 2024Abstract:The subject of features normalization plays an important central role in data representation, characterization, visualization, analysis, comparison, classification, and modeling, as it can substantially influence and be influenced by all of these activities and respective aspects. The selection of an appropriate normalization method needs to take into account the type and characteristics of the involved features, the methods to be used subsequently for the just mentioned data processing, as well as the specific questions being considered. After briefly considering how normalization constitutes one of the many interrelated parts typically involved in data analysis and modeling, the present work addressed the important issue of feature normalization from the perspective of uniform and proportional (right skewed) features and comparison operations. More general right skewed features are also considered in an approximated manner. Several concepts, properties, and results are described and discussed, including the description of a duality relationship between uniform and proportional feature spaces and respective comparisons, specifying conditions for consistency between comparisons in each of the two domains. Two normalization possibilities based on non-centralized dispersion of features are also presented, and also described is a modified version of the Jaccard similarity index which incorporates intrinsically normalization. Preliminary experiments are presented in order to illustrate the developed concepts and methods.
Supervised Pattern Recognition Involving Skewed Feature Densities
Sep 02, 2024



Abstract:Pattern recognition constitutes a particularly important task underlying a great deal of scientific and technologica activities. At the same time, pattern recognition involves several challenges, including the choice of features to represent the data elements, as well as possible respective transformations. In the present work, the classification potential of the Euclidean distance and a dissimilarity index based on the coincidence similarity index are compared by using the k-neighbors supervised classification method respectively to features resulting from several types of transformations of one- and two-dimensional symmetric densities. Given two groups characterized by respective densities without or with overlap, different types of respective transformations are obtained and employed to quantitatively evaluate the performance of k-neighbors methodologies based on the Euclidean distance an coincidence similarity index. More specifically, the accuracy of classifying the intersection point between the densities of two adjacent groups is taken into account for the comparison. Several interesting results are described and discussed, including the enhanced potential of the dissimilarity index for classifying datasets with right skewed feature densities, as well as the identification that the sharpness of the comparison between data elements can be independent of the respective supervised classification performance.
Multilayer Multiset Neuronal Networks -- MMNNs
Aug 28, 2023



Abstract:The coincidence similarity index, based on a combination of the Jaccard and overlap similarity indices, has noticeable properties in comparing and classifying data, including enhanced selectivity and sensitivity, intrinsic normalization, and robustness to data perturbations and outliers. These features allow multiset neurons, which are based on the coincidence similarity operation, to perform effective pattern recognition applications, including the challenging task of image segmentation. A few prototype points have been used in previous related approaches to represent each pattern to be identified, each of them being associated with respective multiset neurons. The segmentation of the regions can then proceed by taking into account the outputs of these neurons. The present work describes multilayer multiset neuronal networks incorporating two or more layers of coincidence similarity neurons. In addition, as a means to improve performance, this work also explores the utilization of counter-prototype points, which are assigned to the image regions to be avoided. This approach is shown to allow effective segmentation of complex regions despite considering only one prototype and one counter-prototype point. As reported here, the balanced accuracy landscapes to be optimized in order to identify the weight of the neurons in subsequent layers have been found to be relatively smooth, while typically involving more than one attraction basin. The use of a simple gradient-based optimization methodology has been demonstrated to effectively train the considered neural networks with several architectures, at least for the given data type, configuration of parameters, and network architecture.
Two Approaches to Supervised Image Segmentation
Aug 03, 2023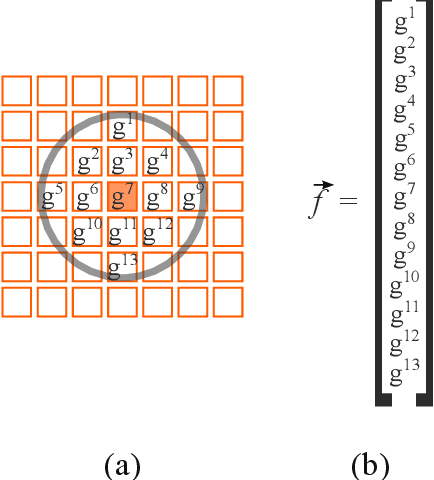



Abstract:Though performed almost effortlessly by humans, segmenting 2D gray-scale or color images in terms of regions of interest (e.g.~background, objects, or portions of objects) constitutes one of the greatest challenges in science and technology as a consequence of the involved dimensionality reduction(3D to 2D), noise, reflections, shades, and occlusions, among many other possible effects. While a large number of interesting related approaches have been suggested along the last decades, it was mainly thanks to the recent development of deep learning that more effective and general solutions have been obtained, currently constituting the basic comparison reference for this type of operation. Also developed recently, a multiset-based methodology has been described that is capable of encouraging image segmentation performance while combining spatial accuracy, stability, and robustness while requiring little computational resources (hardware and/or training and recognition time). The interesting features of the multiset neurons methodology mostly follow from the enhanced selectivity and sensitivity, as well as good robustness to data perturbations and outliers, allowed by the coincidence similarity index on which the multiset approach to supervised image segmentation is based. After describing the deep learning and multiset neurons approaches, the present work develops two comparison experiments between them which are primarily aimed at illustrating their respective main interesting features when applied to the adopted specific type of data and parameter configurations. While the deep learning approach confirmed its potential for performing image segmentation, the alternative multiset methodology allowed for enhanced accuracy while requiring little computational resources.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge