Multilayer Multiset Neuronal Networks -- MMNNs

The coincidence similarity index, based on a combination of the Jaccard and overlap similarity indices, has noticeable properties in comparing and classifying data, including enhanced selectivity and sensitivity, intrinsic normalization, and robustness to data perturbations and outliers. These features allow multiset neurons, which are based on the coincidence similarity operation, to perform effective pattern recognition applications, including the challenging task of image segmentation. A few prototype points have been used in previous related approaches to represent each pattern to be identified, each of them being associated with respective multiset neurons. The segmentation of the regions can then proceed by taking into account the outputs of these neurons. The present work describes multilayer multiset neuronal networks incorporating two or more layers of coincidence similarity neurons. In addition, as a means to improve performance, this work also explores the utilization of counter-prototype points, which are assigned to the image regions to be avoided. This approach is shown to allow effective segmentation of complex regions despite considering only one prototype and one counter-prototype point. As reported here, the balanced accuracy landscapes to be optimized in order to identify the weight of the neurons in subsequent layers have been found to be relatively smooth, while typically involving more than one attraction basin. The use of a simple gradient-based optimization methodology has been demonstrated to effectively train the considered neural networks with several architectures, at least for the given data type, configuration of parameters, and network architecture.

Unraveling the graph structure of tabular datasets through Bayesian and spectral analysis

In the big-data age tabular datasets are being generated and analyzed everywhere. As a consequence, finding and understanding the relationships between the features of these datasets are of great relevance. Here, to encompass these relationships we propose a methodology that maps an entire tabular dataset or just an observation into a weighted directed graph using the Shapley additive explanations technique. With this graph of relationships, we show that the inference of the hierarchical modular structure obtained by the nested stochastic block model (nSBM) as well as the study of the spectral space of the magnetic Laplacian can help us identify the classes of features and unravel non-trivial relationships. As a case study, we analyzed a socioeconomic survey conducted with students in Brazil: the PeNSE survey. The spectral embedding of the columns suggested that questions related to physical activities form a separate group. The application of the nSBM approach, corroborated with that and allowed complementary findings about the modular structure: some groups of questions showed a high adherence with the divisions qualitatively defined by the designers of the survey. However, questions from the class \textit{Safety} were partly grouped by our method in the class \textit{Drugs}. Surprisingly, by inspecting these questions, we observed that they were related to both these topics, suggesting an alternative interpretation of these questions. Our method can provide guidance for tabular data analysis as well as the design of future surveys.

Scilab and SIP for Image Processing

This paper is an overview of Image Processing and Analysis using Scilab, a free prototyping environment for numerical calculations similar to Matlab. We demonstrate the capabilities of SIP -- the Scilab Image Processing Toolbox -- which extends Scilab with many functions to read and write images in over 100 major file formats, including PNG, JPEG, BMP, and TIFF. It also provides routines for image filtering, edge detection, blurring, segmentation, shape analysis, and image recognition. Basic directions to install Scilab and SIP are given, and also a mini-tutorial on Scilab. Three practical examples of image analysis are presented, in increasing degrees of complexity, showing how advanced image analysis techniques seems uncomplicated in this environment.

A Complex Networks Approach for Data Clustering

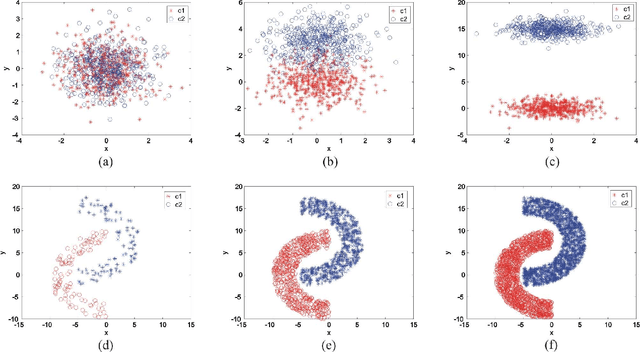
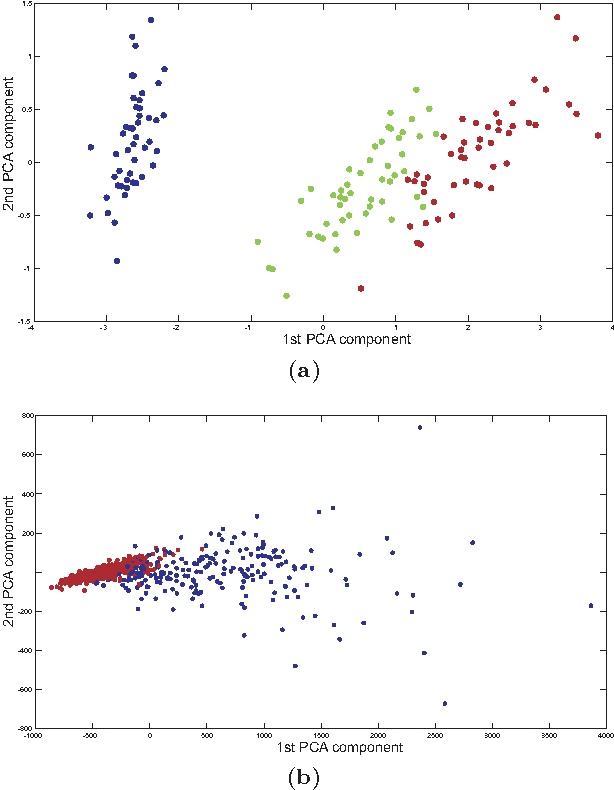
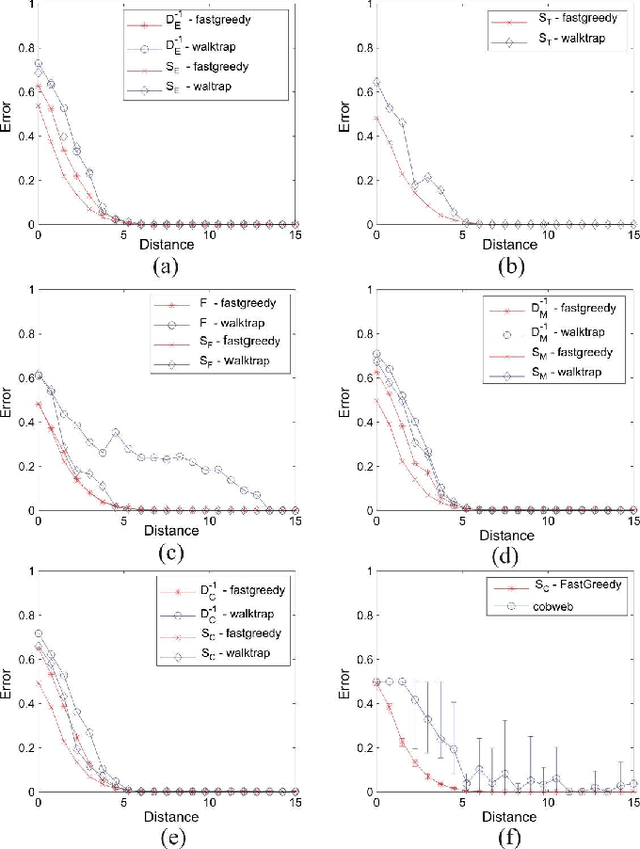
Many methods have been developed for data clustering, such as k-means, expectation maximization and algorithms based on graph theory. In this latter case, graphs are generally constructed by taking into account the Euclidian distance as a similarity measure, and partitioned using spectral methods. However, these methods are not accurate when the clusters are not well separated. In addition, it is not possible to automatically determine the number of clusters. These limitations can be overcome by taking into account network community identification algorithms. In this work, we propose a methodology for data clustering based on complex networks theory. We compare different metrics for quantifying the similarity between objects and take into account three community finding techniques. This approach is applied to two real-world databases and to two sets of artificially generated data. By comparing our method with traditional clustering approaches, we verify that the proximity measures given by the Chebyshev and Manhattan distances are the most suitable metrics to quantify the similarity between objects. In addition, the community identification method based on the greedy optimization provides the smallest misclassification rates.

Complex Networks: New Concepts and Tools for Real-Time Imaging and Vision

This article discusses how concepts and methods of complex networks can be applied to real-time imaging and computer vision. After a brief introduction of complex networks basic concepts, their use as means to represent and characterize images, as well as for modeling visual saliency, are briefly described. The possibility to apply complex networks in order to model and simulate the performance of parallel and distributed computing systems for performance of visual methods is also proposed.

Learning about knowledge: A complex network approach

This article describes an approach to modeling knowledge acquisition in terms of walks along complex networks. Each subset of knowledge is represented as a node, and relations between such knowledge are expressed as edges. Two types of edges are considered, corresponding to free and conditional transitions. The latter case implies that a node can only be reached after visiting previously a set of nodes (the required conditions). The process of knowledge acquisition can then be simulated by considering the number of nodes visited as a single agent moves along the network, starting from its lowest layer. It is shown that hierarchical networks, i.e. networks composed of successive interconnected layers, arise naturally as a consequence of compositions of the prerequisite relationships between the nodes. In order to avoid deadlocks, i.e. unreachable nodes, the subnetwork in each layer is assumed to be a connected component. Several configurations of such hierarchical knowledge networks are simulated and the performance of the moving agent quantified in terms of the percentage of visited nodes after each movement. The Barab\'asi-Albert and random models are considered for the layer and interconnecting subnetworks. Although all subnetworks in each realization have the same number of nodes, several interconnectivities, defined by the average node degree of the interconnection networks, have been considered. Two visiting strategies are investigated: random choice among the existing edges and preferential choice to so far untracked edges. A series of interesting results are obtained, including the identification of a series of plateaux of knowledge stagnation in the case of the preferential movements strategy in presence of conditional edges.

A Fast and Accurate Nonlinear Spectral Method for Image Recognition and Registration

This article addresses the problem of two- and higher dimensional pattern matching, i.e. the identification of instances of a template within a larger signal space, which is a form of registration. Unlike traditional correlation, we aim at obtaining more selective matchings by considering more strict comparisons of gray-level intensity. In order to achieve fast matching, a nonlinear thresholded version of the fast Fourier transform is applied to a gray-level decomposition of the original 2D image. The potential of the method is substantiated with respect to real data involving the selective identification of neuronal cell bodies in gray-level images.

Statistical Mechanics Characterization of Neuronal Mosaics

The spatial distribution of neuronal cells is an important requirement for achieving proper neuronal function in several parts of the nervous system of most animals. For instance, specific distribution of photoreceptors and related neuronal cells, particularly the ganglion cells, in mammal's retina is required in order to properly sample the projected scene. This work presents how two concepts from the areas of statistical mechanics and complex systems, namely the \emph{lacunarity} and the \emph{multiscale entropy} (i.e. the entropy calculated over progressively diffused representations of the cell mosaic), have allowed effective characterization of the spatial distribution of retinal cells.

Correlation over Decomposed Signals: A Non-Linear Approach to Fast and Effective Sequences Comparison

A novel non-linear approach to fast and effective comparison of sequences is presented, compared to the traditional cross-correlation operator, and illustrated with respect to DNA sequences.