Guilherme Ferraz de Arruda
A Complex Networks Approach for Data Clustering
Jan 26, 2011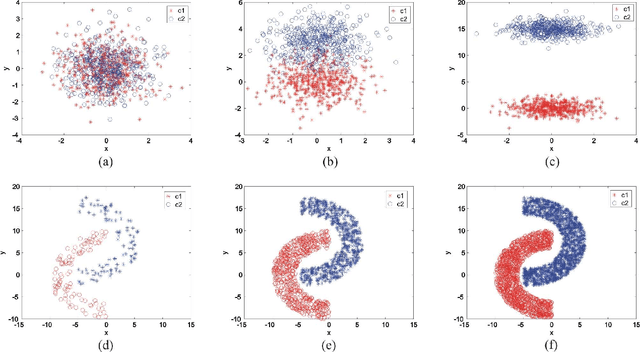
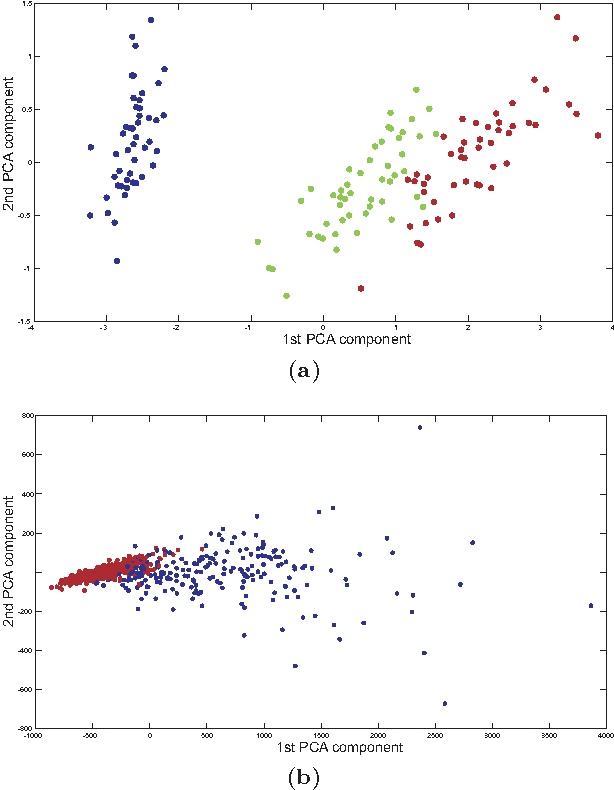

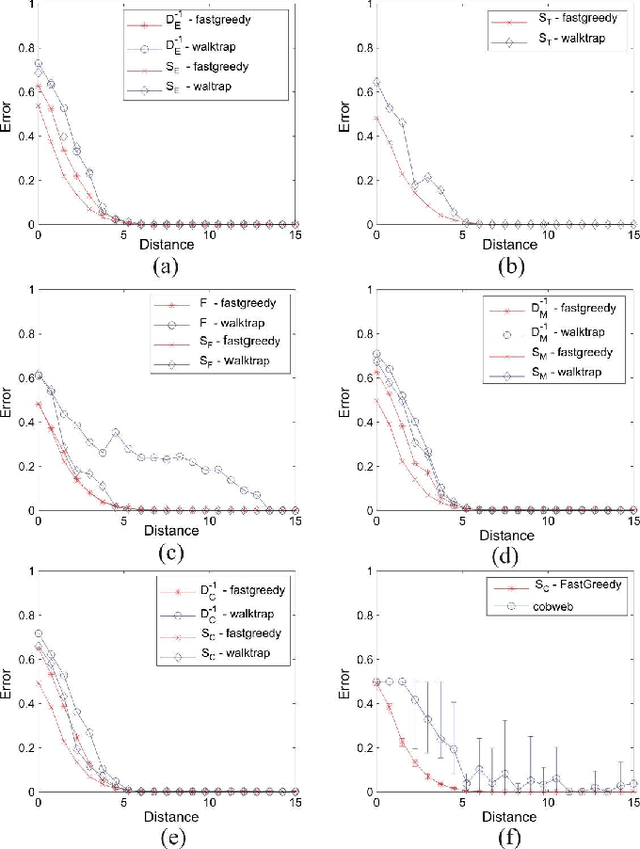
Abstract:Many methods have been developed for data clustering, such as k-means, expectation maximization and algorithms based on graph theory. In this latter case, graphs are generally constructed by taking into account the Euclidian distance as a similarity measure, and partitioned using spectral methods. However, these methods are not accurate when the clusters are not well separated. In addition, it is not possible to automatically determine the number of clusters. These limitations can be overcome by taking into account network community identification algorithms. In this work, we propose a methodology for data clustering based on complex networks theory. We compare different metrics for quantifying the similarity between objects and take into account three community finding techniques. This approach is applied to two real-world databases and to two sets of artificially generated data. By comparing our method with traditional clustering approaches, we verify that the proximity measures given by the Chebyshev and Manhattan distances are the most suitable metrics to quantify the similarity between objects. In addition, the community identification method based on the greedy optimization provides the smallest misclassification rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge