Scale-free networks: improved inference

The power-law distribution plays a crucial role in complex networks as well as various applied sciences. Investigating whether the degree distribution of a network follows a power-law distribution is an important concern. The commonly used inferential methods for estimating the model parameters often yield biased estimates, which can lead to the rejection of the hypothesis that a model conforms to a power-law. In this paper, we discuss improved methods that utilize Bayesian inference to obtain accurate estimates and precise credibility intervals. The inferential methods are derived for both continuous and discrete distributions. These methods reveal that objective Bayesian approaches return nearly unbiased estimates for the parameters of both models. Notably, in the continuous case, we identify an explicit posterior distribution. This work enhances the power of goodness-of-fit tests, enabling us to accurately discern whether a network or any other dataset adheres to a power-law distribution. We apply the proposed approach to fit degree distributions for more than 5,000 synthetic networks and over 3,000 real networks. The results indicate that our method is more suitable in practice, as it yields a frequency of acceptance close to the specified nominal level.

Machine learning in physics: a short guide

Machine learning is a rapidly growing field with the potential to revolutionize many areas of science, including physics. This review provides a brief overview of machine learning in physics, covering the main concepts of supervised, unsupervised, and reinforcement learning, as well as more specialized topics such as causal inference, symbolic regression, and deep learning. We present some of the principal applications of machine learning in physics and discuss the associated challenges and perspectives.

Forecasting new diseases in low-data settings using transfer learning

Recent infectious disease outbreaks, such as the COVID-19 pandemic and the Zika epidemic in Brazil, have demonstrated both the importance and difficulty of accurately forecasting novel infectious diseases. When new diseases first emerge, we have little knowledge of the transmission process, the level and duration of immunity to reinfection, or other parameters required to build realistic epidemiological models. Time series forecasts and machine learning, while less reliant on assumptions about the disease, require large amounts of data that are also not available in early stages of an outbreak. In this study, we examine how knowledge of related diseases can help make predictions of new diseases in data-scarce environments using transfer learning. We implement both an empirical and a theoretical approach. Using empirical data from Brazil, we compare how well different machine learning models transfer knowledge between two different disease pairs: (i) dengue and Zika, and (ii) influenza and COVID-19. In the theoretical analysis, we generate data using different transmission and recovery rates with an SIR compartmental model, and then compare the effectiveness of different transfer learning methods. We find that transfer learning offers the potential to improve predictions, even beyond a model based on data from the target disease, though the appropriate source disease must be chosen carefully. While imperfect, these models offer an additional input for decision makers during pandemic response.

EEG functional connectivity and deep learning for automatic diagnosis of brain disorders: Alzheimer's disease and schizophrenia

Mental disorders are among the leading causes of disability worldwide. The first step in treating these conditions is to obtain an accurate diagnosis, but the absence of established clinical tests makes this task challenging. Machine learning algorithms can provide a possible solution to this problem, as we describe in this work. We present a method for the automatic diagnosis of mental disorders based on the matrix of connections obtained from EEG time series and deep learning. We show that our approach can classify patients with Alzheimer's disease and schizophrenia with a high level of accuracy. The comparison with the traditional cases, that use raw EEG time series, shows that our method provides the highest precision. Therefore, the application of deep neural networks on data from brain connections is a very promising method to the diagnosis of neurological disorders.

Neural Networks for Dengue Prediction: A Systematic Review

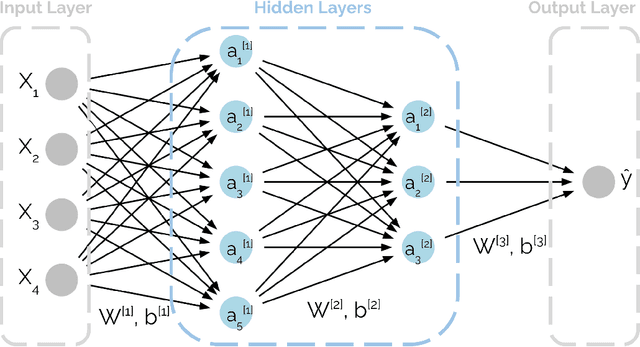
Due to a lack of treatments and universal vaccine, early forecasts of Dengue are an important tool for disease control. Neural networks are powerful predictive models that have made contributions to many areas of public health. In this systematic review, we provide an introduction to the neural networks relevant to Dengue forecasting and review their applications in the literature. The objective is to help inform model design for future work. Following the PRISMA guidelines, we conduct a systematic search of studies that use neural networks to forecast Dengue in human populations. We summarize the relative performance of neural networks and comparator models, model architectures and hyper-parameters, as well as choices of input features. Nineteen papers were included. Most studies implement shallow neural networks using historical Dengue incidence and meteorological input features. Prediction horizons tend to be short. Building on the strengths of neural networks, most studies use granular observations at the city or sub-national level. Performance of neural networks relative to comparators such as Support Vector Machines varies across study contexts. The studies suggest that neural networks can provide good predictions of Dengue and should be included in the set of candidate models. The use of convolutional, recurrent, or deep networks is relatively unexplored but offers promising avenues for further research, as does the use of a broader set of input features such as social media or mobile phone data.

Pattern Recognition Approach to Violin Shapes of MIMO database

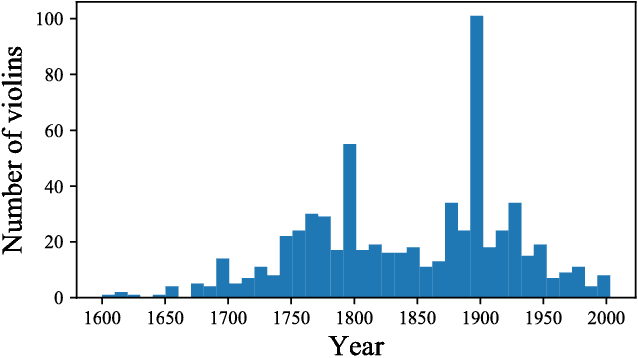
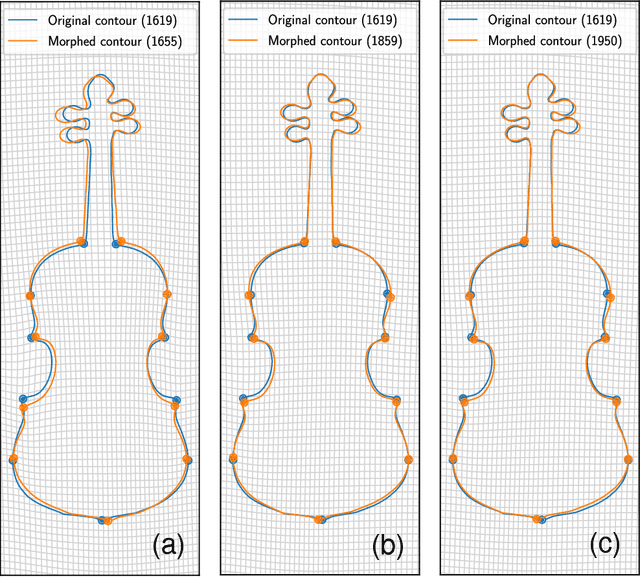
Since the landmarks established by the Cremonese school in the 16th century, the history of violin design has been marked by experimentation. While great effort has been invested since the early 19th century by the scientific community on researching violin acoustics, substantially less attention has been given to the statistical characterization of how the violin shape evolved over time. In this paper we study the morphology of violins retrieved from the Musical Instrument Museums Online (MIMO) database -- the largest freely accessible platform providing information about instruments held in public museums. From the violin images, we derive a set of measurements that reflect relevant geometrical features of the instruments. The application of Principal Component Analysis (PCA) uncovered similarities between violin makers and their respective copyists, as well as among luthiers belonging to the same family lineage, in the context of historical narrative. Combined with a time-windowed approach, thin plate splines visualizations revealed that the average violin outline has remained mostly stable over time, not adhering to any particular trends of design across different periods in music history.

Clustering Algorithms: A Comparative Approach

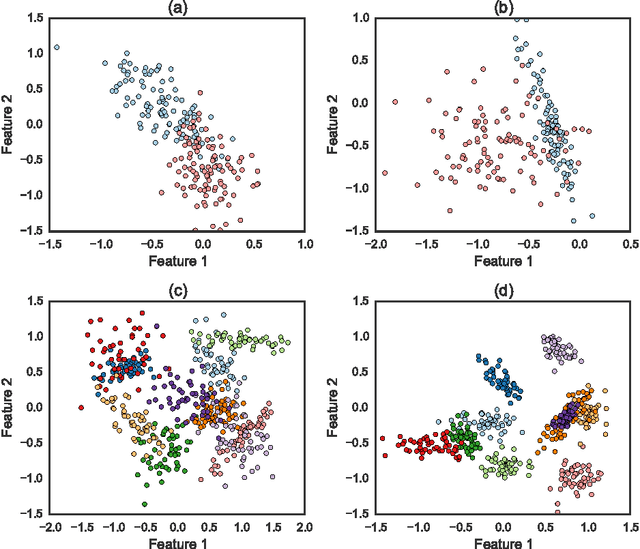
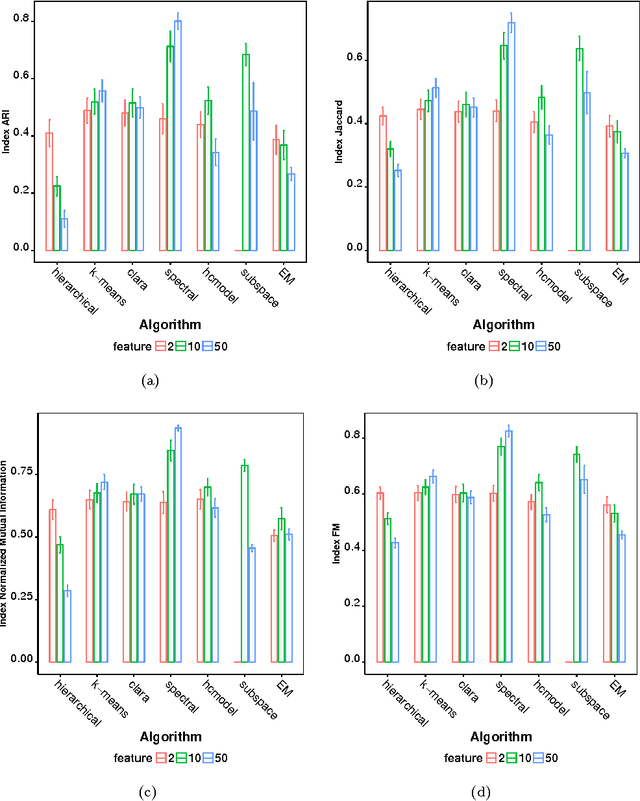
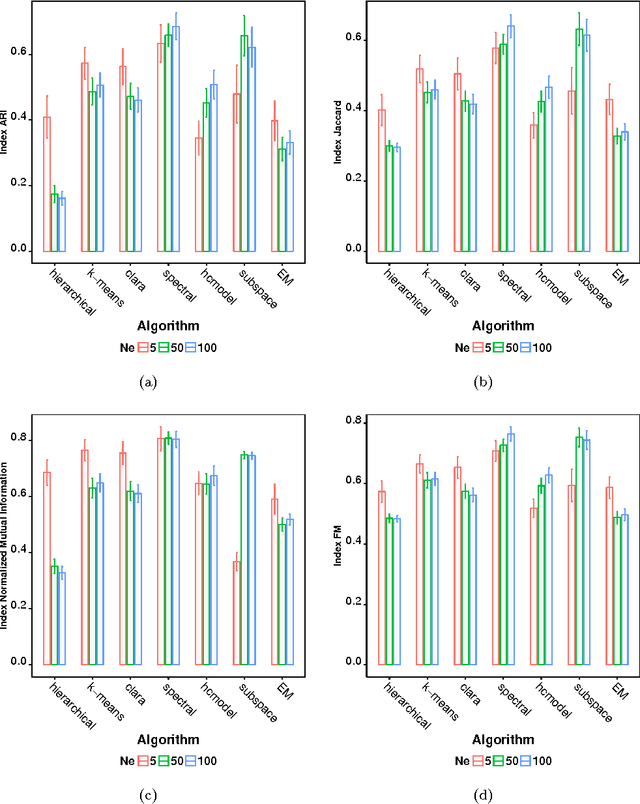
Many real-world systems can be studied in terms of pattern recognition tasks, so that proper use (and understanding) of machine learning methods in practical applications becomes essential. While a myriad of classification methods have been proposed, there is no consensus on which methods are more suitable for a given dataset. As a consequence, it is important to comprehensively compare methods in many possible scenarios. In this context, we performed a systematic comparison of 7 well-known clustering methods available in the R language. In order to account for the many possible variations of data, we considered artificial datasets with several tunable properties (number of classes, separation between classes, etc). In addition, we also evaluated the sensitivity of the clustering methods with regard to their parameters configuration. The results revealed that, when considering the default configurations of the adopted methods, the spectral approach usually outperformed the other clustering algorithms. We also found that the default configuration of the adopted implementations was not accurate. In these cases, a simple approach based on random selection of parameters values proved to be a good alternative to improve the performance. All in all, the reported approach provides subsidies guiding the choice of clustering algorithms.

Complex systems: features, similarity and connectivity

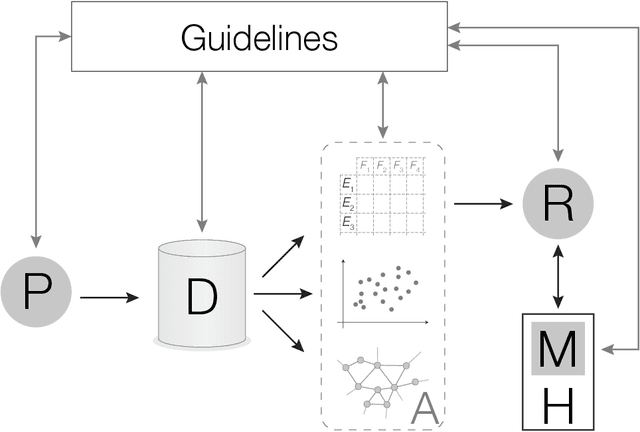
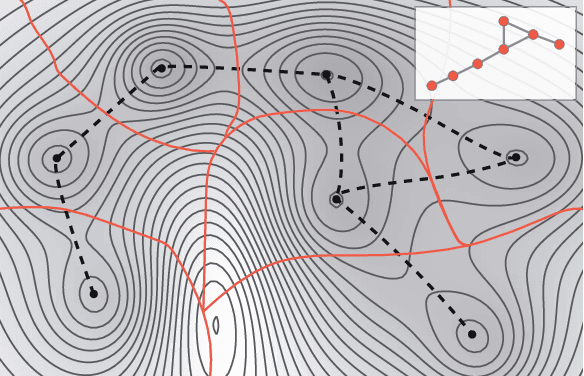
The increasing interest in complex networks research has been a consequence of several intrinsic features of this area, such as the generality of the approach to represent and model virtually any discrete system, and the incorporation of concepts and methods deriving from many areas, from statistical physics to sociology, which are often used in an independent way. Yet, for this same reason, it would be desirable to integrate these various aspects into a more coherent and organic framework, which would imply in several benefits normally allowed by the systematization in science, including the identification of new types of problems and the cross-fertilization between fields. More specifically, the identification of the main areas to which the concepts frequently used in complex networks can be applied paves the way to adopting and applying a larger set of concepts and methods deriving from those respective areas. Among the several areas that have been used in complex networks research, pattern recognition, optimization, linear algebra, and time series analysis seem to play a more basic and recurrent role. In the present manuscript, we propose a systematic way to integrate the concepts from these diverse areas regarding complex networks research. In order to do so, we start by grouping the multidisciplinary concepts into three main groups, namely features, similarity, and network connectivity. Then we show that several of the analysis and modeling approaches to complex networks can be thought as a composition of maps between these three groups, with emphasis on nine main types of mappings, which are presented and illustrated. Such a systematization of principles and approaches also provides an opportunity to review some of the most closely related works in the literature, which is also developed in this article.

A Complex Networks Approach for Data Clustering

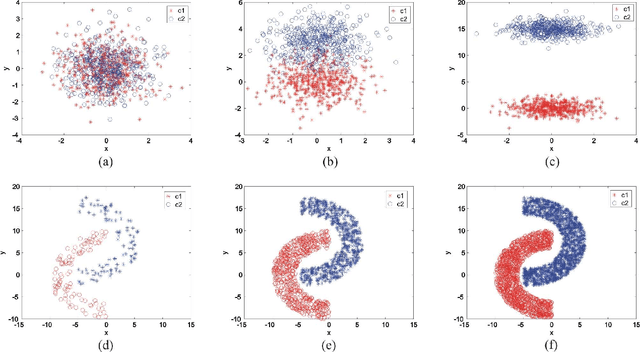
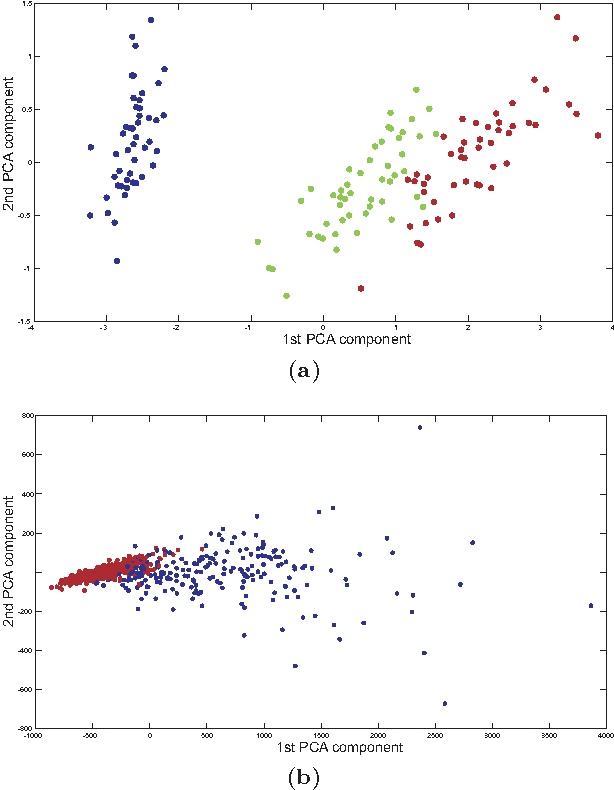
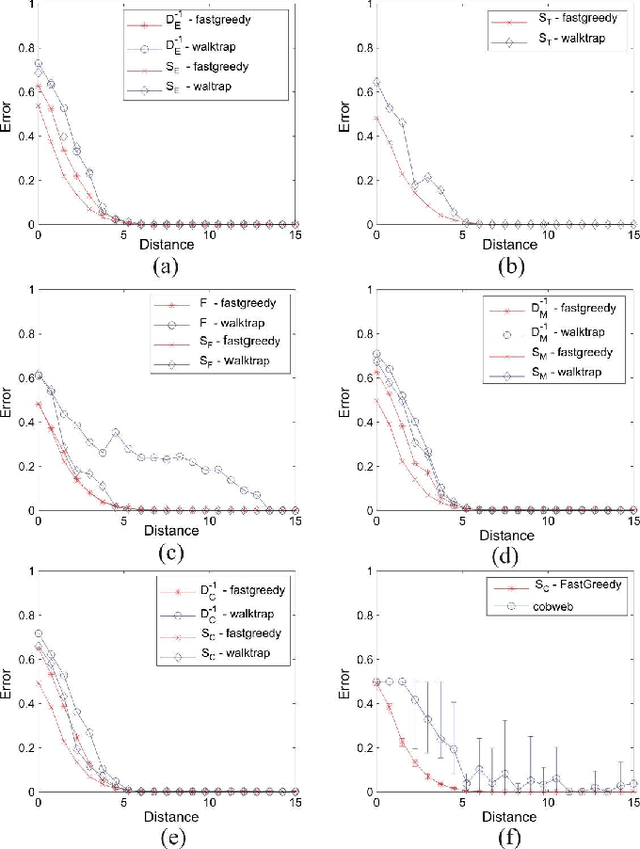
Many methods have been developed for data clustering, such as k-means, expectation maximization and algorithms based on graph theory. In this latter case, graphs are generally constructed by taking into account the Euclidian distance as a similarity measure, and partitioned using spectral methods. However, these methods are not accurate when the clusters are not well separated. In addition, it is not possible to automatically determine the number of clusters. These limitations can be overcome by taking into account network community identification algorithms. In this work, we propose a methodology for data clustering based on complex networks theory. We compare different metrics for quantifying the similarity between objects and take into account three community finding techniques. This approach is applied to two real-world databases and to two sets of artificially generated data. By comparing our method with traditional clustering approaches, we verify that the proximity measures given by the Chebyshev and Manhattan distances are the most suitable metrics to quantify the similarity between objects. In addition, the community identification method based on the greedy optimization provides the smallest misclassification rates.