VessShape: Few-shot 2D blood vessel segmentation by leveraging shape priors from synthetic images

Semantic segmentation of blood vessels is an important task in medical image analysis, but its progress is often hindered by the scarcity of large annotated datasets and the poor generalization of models across different imaging modalities. A key aspect is the tendency of Convolutional Neural Networks (CNNs) to learn texture-based features, which limits their performance when applied to new domains with different visual characteristics. We hypothesize that leveraging geometric priors of vessel shapes, such as their tubular and branching nature, can lead to more robust and data-efficient models. To investigate this, we introduce VessShape, a methodology for generating large-scale 2D synthetic datasets designed to instill a shape bias in segmentation models. VessShape images contain procedurally generated tubular geometries combined with a wide variety of foreground and background textures, encouraging models to learn shape cues rather than textures. We demonstrate that a model pre-trained on VessShape images achieves strong few-shot segmentation performance on two real-world datasets from different domains, requiring only four to ten samples for fine-tuning. Furthermore, the model exhibits notable zero-shot capabilities, effectively segmenting vessels in unseen domains without any target-specific training. Our results indicate that pre-training with a strong shape bias can be an effective strategy to overcome data scarcity and improve model generalization in blood vessel segmentation.

An Analysis of the Influence of Transfer Learning When Measuring the Tortuosity of Blood Vessels

Characterizing blood vessels in digital images is important for the diagnosis of many types of diseases as well as for assisting current researches regarding vascular systems. The automated analysis of blood vessels typically requires the identification, or segmentation, of the blood vessels in an image or a set of images, which is usually a challenging task. Convolutional Neural Networks (CNNs) have been shown to provide excellent results regarding the segmentation of blood vessels. One important aspect of CNNs is that they can be trained on large amounts of data and then be made available, for instance, in image processing software for wide use. The pre-trained CNNs can then be easily applied in downstream blood vessel characterization tasks such as the calculation of the length, tortuosity, or caliber of the blood vessels. Yet, it is still unclear if pre-trained CNNs can provide robust, unbiased, results on downstream tasks when applied to datasets that they were not trained on. Here, we focus on measuring the tortuosity of blood vessels and investigate to which extent CNNs may provide biased tortuosity values even after fine-tuning the network to the new dataset under study. We show that the tortuosity values obtained by a CNN trained from scratch on a dataset may not agree with those obtained by a fine-tuned network that was pre-trained on a dataset having different tortuosity statistics. In addition, we show that the improvement in segmentation performance when fine-tuning the network does not necessarily lead to a respective improvement on the estimation of the tortuosity. To mitigate the aforementioned issues, we propose the application of specific data augmentation techniques even in situations where they do not improve segmentation performance.

Revisiting Agglomerative Clustering

In data clustering, emphasis is often placed in finding groups of points. An equally important subject concerns the avoidance of false positives. As it could be expected, these two goals oppose one another, in the sense that emphasis on finding clusters tends to imply in higher probability of obtaining false positives. The present work addresses this problem considering some traditional agglomerative methods, namely single, average, median, complete, centroid and Ward's applied to unimodal and bimodal datasets following uniform, gaussian, exponential and power-law distributions. More importantly, we adopt a generic model of clusters involving a higher density core surrounded by a transition zone, followed by a sparser set of outliers. Combined with preliminary specification of the size of the expected clusters, this model paved the way to the implementation of an objective means for identifying the clusters from dendrograms. In addition, the adopted model also allowed the relevance of the detected clusters to be estimated in terms of the height of the subtrees corresponding to the identified clusters. More specifically, the lower this height, the more compact and relevant the clusters tend to be. Several interesting results have been obtained, including the tendency of several of the considered methods to detect two clusters in unimodal data. The single-linkage method has been found to provide the best resilience to this tendency. In addition, several methods tended to detect clusters that do not correspond directly to the cores, therefore characterized by lower relevance. The possibility of identifying the type of distribution of points from the adopted measurements was also investigated.

Clustering Algorithms: A Comparative Approach

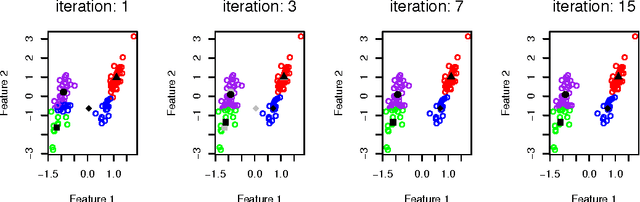
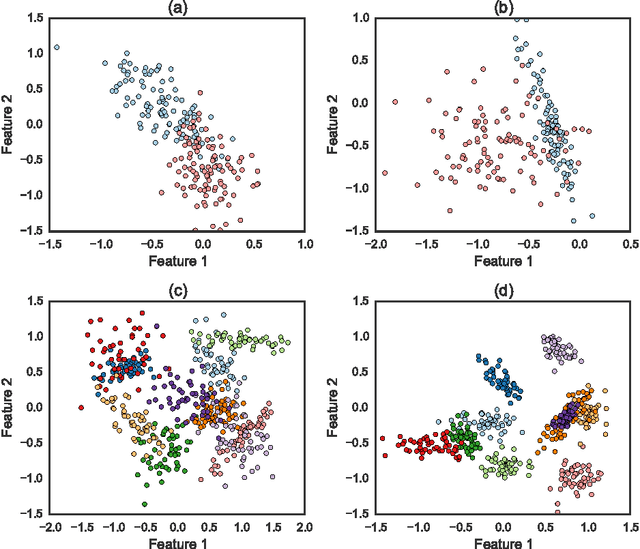
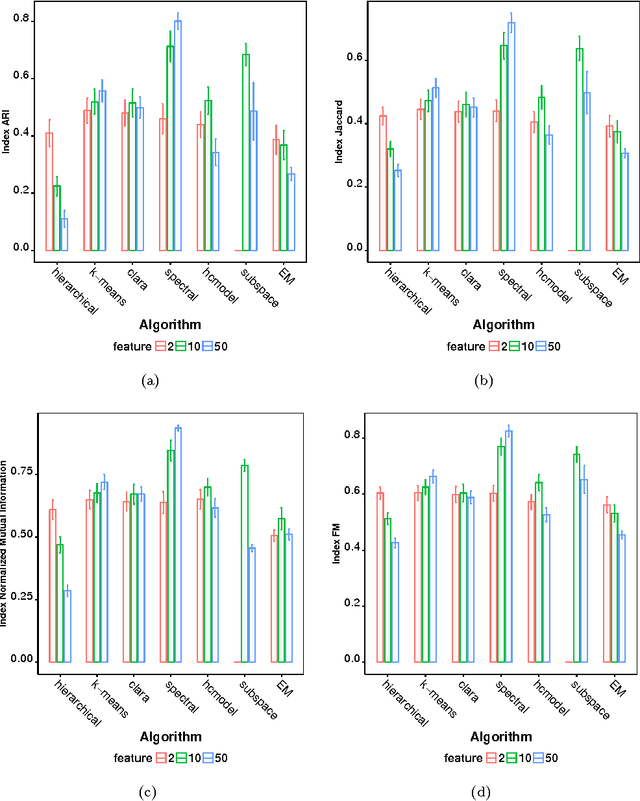
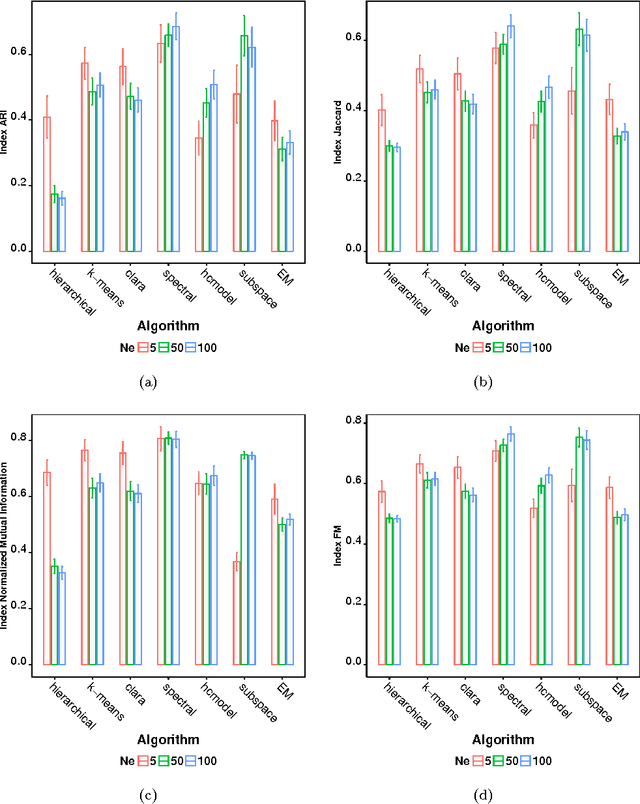
Many real-world systems can be studied in terms of pattern recognition tasks, so that proper use (and understanding) of machine learning methods in practical applications becomes essential. While a myriad of classification methods have been proposed, there is no consensus on which methods are more suitable for a given dataset. As a consequence, it is important to comprehensively compare methods in many possible scenarios. In this context, we performed a systematic comparison of 7 well-known clustering methods available in the R language. In order to account for the many possible variations of data, we considered artificial datasets with several tunable properties (number of classes, separation between classes, etc). In addition, we also evaluated the sensitivity of the clustering methods with regard to their parameters configuration. The results revealed that, when considering the default configurations of the adopted methods, the spectral approach usually outperformed the other clustering algorithms. We also found that the default configuration of the adopted implementations was not accurate. In these cases, a simple approach based on random selection of parameters values proved to be a good alternative to improve the performance. All in all, the reported approach provides subsidies guiding the choice of clustering algorithms.

Complex systems: features, similarity and connectivity

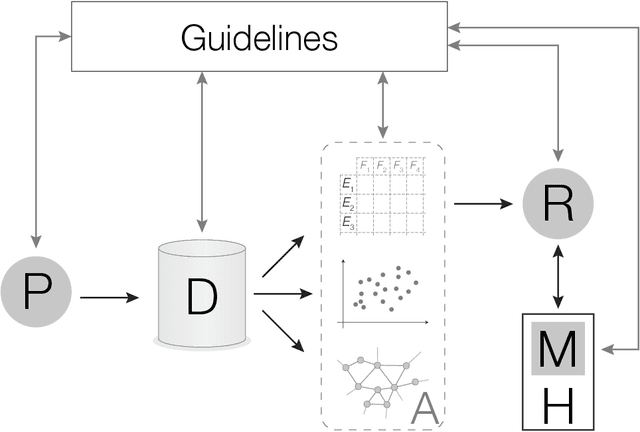
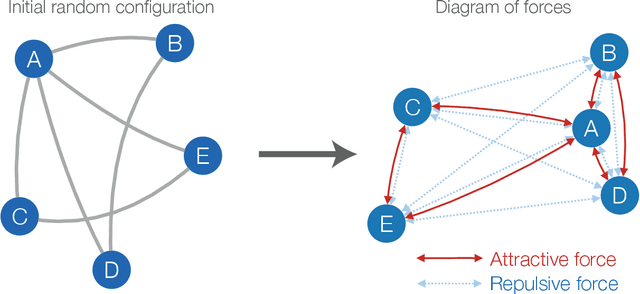
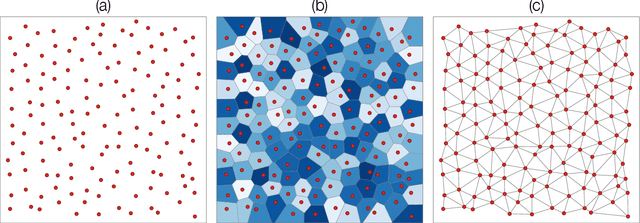
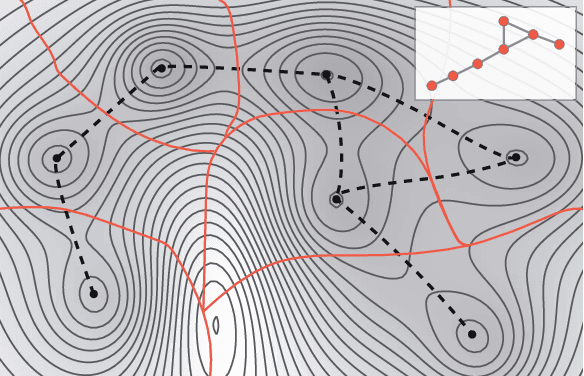
The increasing interest in complex networks research has been a consequence of several intrinsic features of this area, such as the generality of the approach to represent and model virtually any discrete system, and the incorporation of concepts and methods deriving from many areas, from statistical physics to sociology, which are often used in an independent way. Yet, for this same reason, it would be desirable to integrate these various aspects into a more coherent and organic framework, which would imply in several benefits normally allowed by the systematization in science, including the identification of new types of problems and the cross-fertilization between fields. More specifically, the identification of the main areas to which the concepts frequently used in complex networks can be applied paves the way to adopting and applying a larger set of concepts and methods deriving from those respective areas. Among the several areas that have been used in complex networks research, pattern recognition, optimization, linear algebra, and time series analysis seem to play a more basic and recurrent role. In the present manuscript, we propose a systematic way to integrate the concepts from these diverse areas regarding complex networks research. In order to do so, we start by grouping the multidisciplinary concepts into three main groups, namely features, similarity, and network connectivity. Then we show that several of the analysis and modeling approaches to complex networks can be thought as a composition of maps between these three groups, with emphasis on nine main types of mappings, which are presented and illustrated. Such a systematization of principles and approaches also provides an opportunity to review some of the most closely related works in the literature, which is also developed in this article.