Disentangling homophily, community structure and triadic closure in networks
Paper and Code
Jan 10, 2021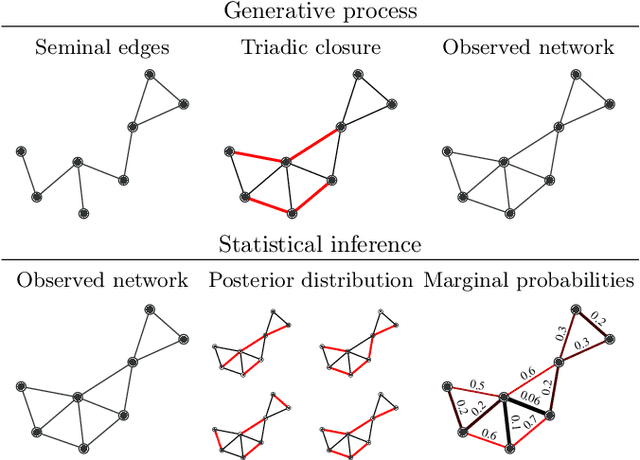
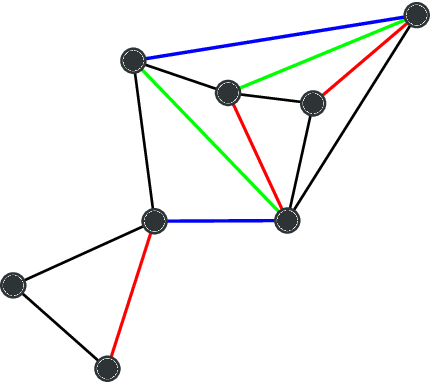
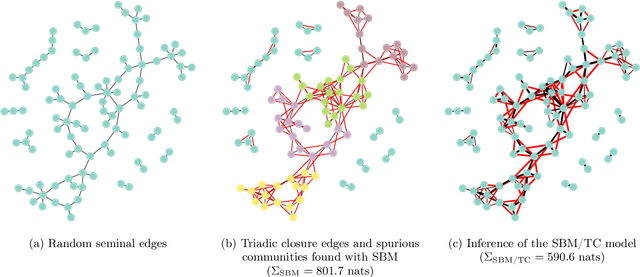
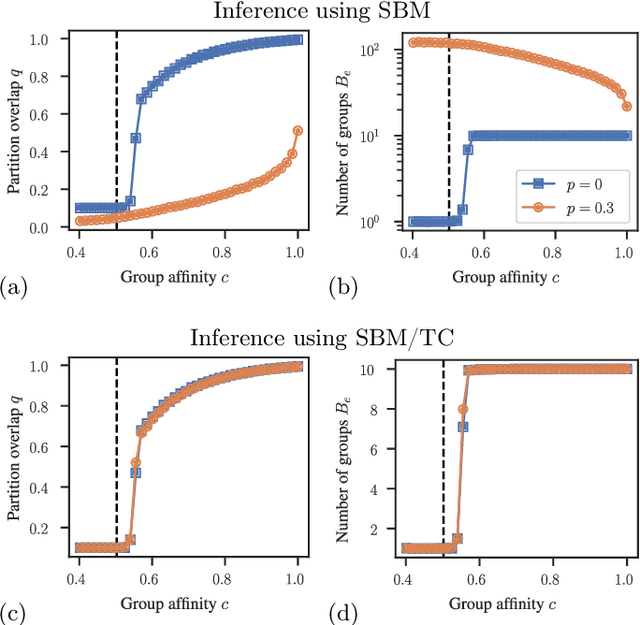
Network homophily, the tendency of similar nodes to be connected, and transitivity, the tendency of two nodes being connected if they share a common neighbor, are conflated properties in network analysis, since one mechanism can drive the other. Here we present a generative model and corresponding inference procedure that is capable of distinguishing between both mechanisms. Our approach is based on a variation of the stochastic block model (SBM) with the addition of triadic closure edges, and its inference can identify the most plausible mechanism responsible for the existence of every edge in the network, in addition to the underlying community structure itself. We show how the method can evade the detection of spurious communities caused solely by the formation of triangles in the network, and how it can improve the performance of link prediction when compared to the pure version of the SBM without triadic closure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge