Rankings from multimodal pairwise comparisons
Paper and Code
Jun 27, 2022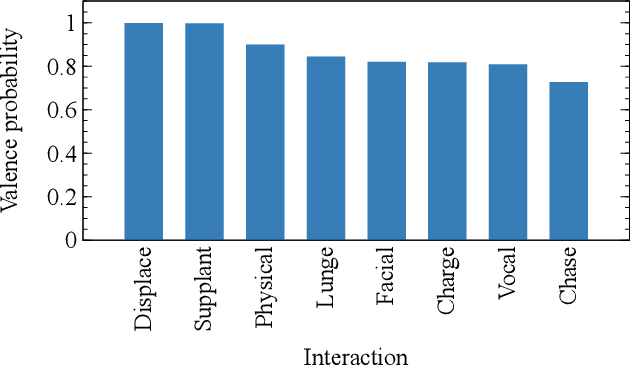
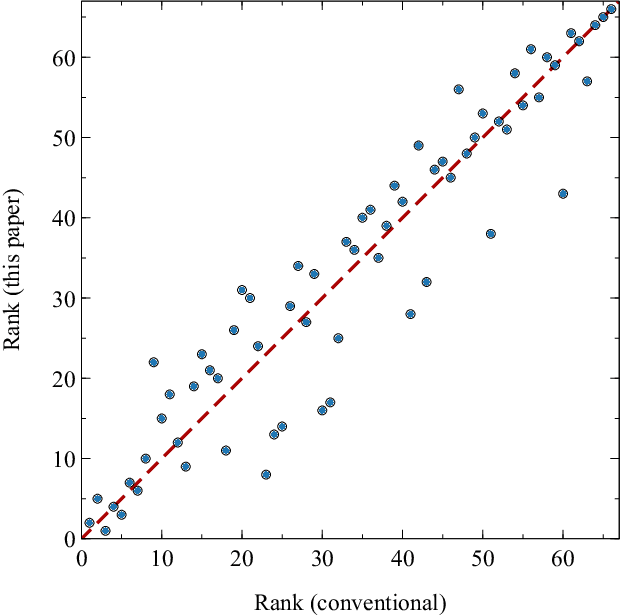
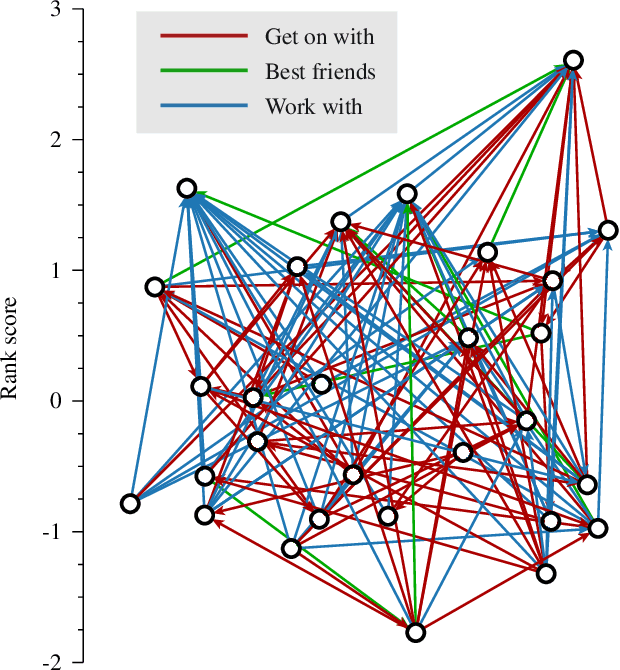
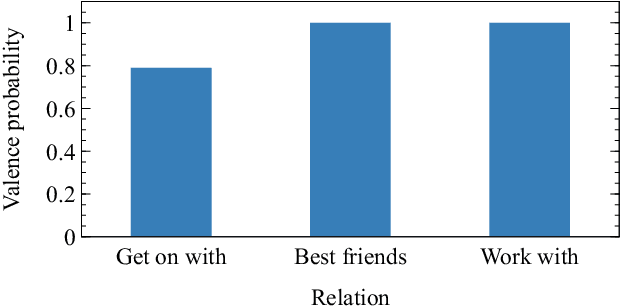
The task of ranking individuals or teams, based on a set of comparisons between pairs, arises in various contexts, including sporting competitions and the analysis of dominance hierarchies among animals and humans. Given data on which competitors beat which others, the challenge is to rank the competitors from best to worst. Here we study the problem of computing rankings when there are multiple, potentially conflicting modes of comparison, such as multiple types of dominance behaviors among animals. We assume that we do not know a priori what information each behavior conveys about the ranking, or even whether they convey any information at all. Nonetheless we show that it is possible to compute a ranking in this situation and present a fast method for doing so, based on a combination of an expectation-maximization algorithm and a modified Bradley-Terry model. We give a selection of example applications to both animal and human competition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge