Approximate sampling and estimation of partition functions using neural networks
Paper and Code
Sep 21, 2022
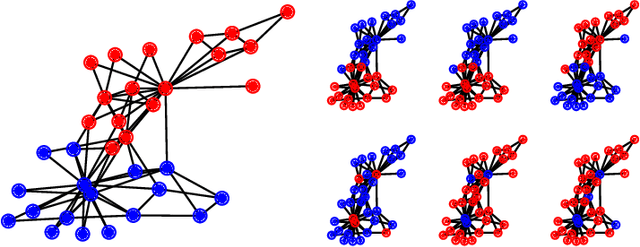
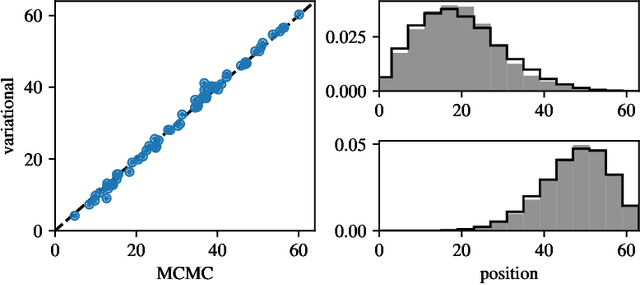
We consider the closely related problems of sampling from a distribution known up to a normalizing constant, and estimating said normalizing constant. We show how variational autoencoders (VAEs) can be applied to this task. In their standard applications, VAEs are trained to fit data drawn from an intractable distribution. We invert the logic and train the VAE to fit a simple and tractable distribution, on the assumption of a complex and intractable latent distribution, specified up to normalization. This procedure constructs approximations without the use of training data or Markov chain Monte Carlo sampling. We illustrate our method on three examples: the Ising model, graph clustering, and ranking.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge