Detectability of hierarchical communities in networks

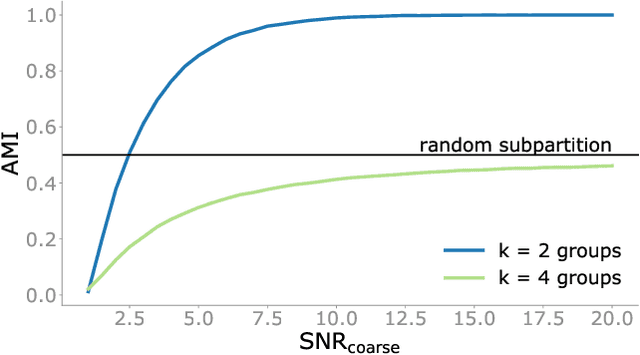
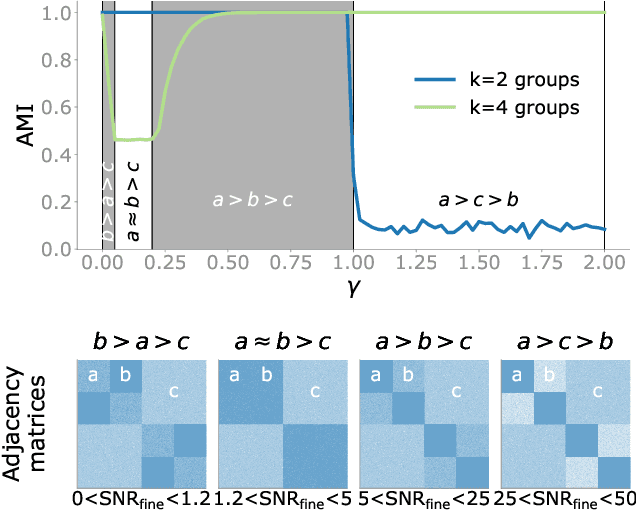
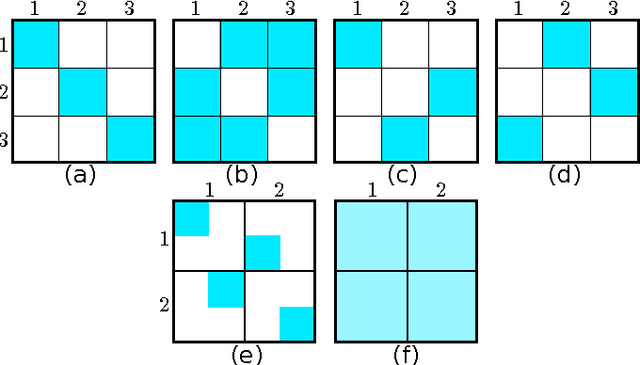
We study the problem of recovering a planted hierarchy of partitions in a network. The detectability of a single planted partition has previously been analysed in detail and a phase transition has been identified below which the partition cannot be detected. Here we show that, in the hierarchical setting, there exist additional phases in which the presence of multiple consistent partitions can either help or hinder detection. Accordingly, the detectability limit for non-hierarchical partitions typically provides insufficient information about the detectability of the complete hierarchical structure, as we highlight with several constructive examples.

Hierarchical community structure in networks

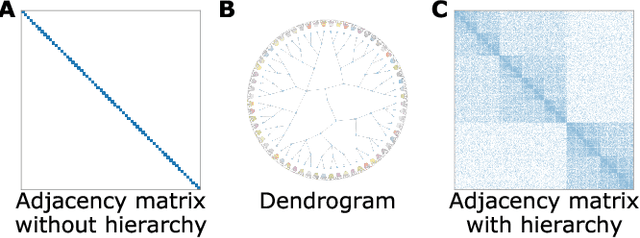
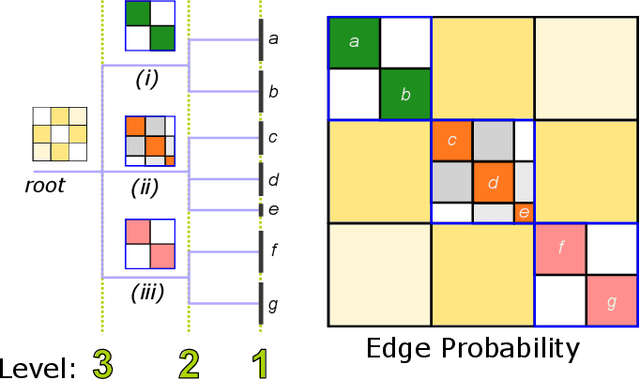
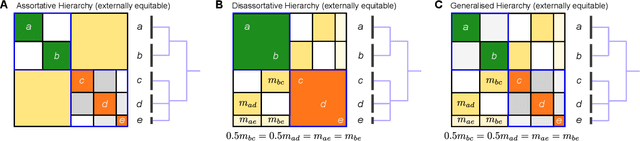
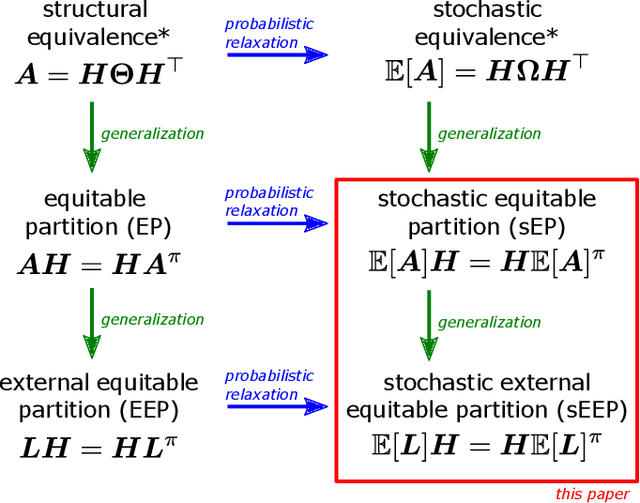
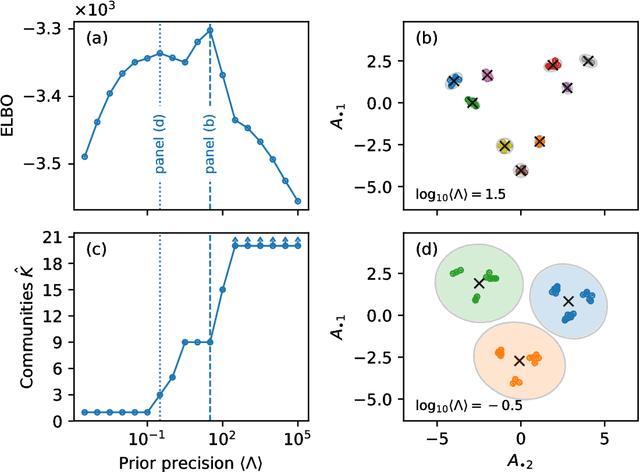
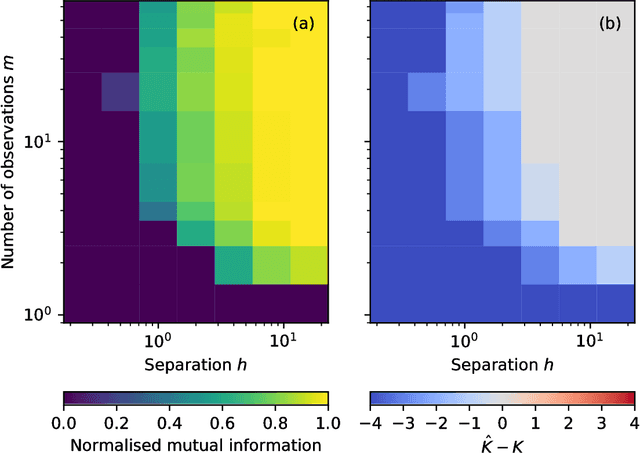
Modular and hierarchical structures are pervasive in real-world complex systems. A great deal of effort has gone into trying to detect and study these structures. Important theoretical advances in the detection of modular, or "community", structures have included identifying fundamental limits of detectability by formally defining community structure using probabilistic generative models. Detecting hierarchical community structure introduces additional challenges alongside those inherited from community detection. Here we present a theoretical study on hierarchical community structure in networks, which has thus far not received the same rigorous attention. We address the following questions: 1)~How should we define a valid hierarchy of communities? 2)~How should we determine if a hierarchical structure exists in a network? and 3)~how can we detect hierarchical structure efficiently? We approach these questions by introducing a definition of hierarchy based on the concept of stochastic externally equitable partitions and their relation to probabilistic models, such as the popular stochastic block model. We enumerate the challenges involved in detecting hierarchies and, by studying the spectral properties of hierarchical structure, present an efficient and principled method for detecting them.

Community detection in networks with unobserved edges

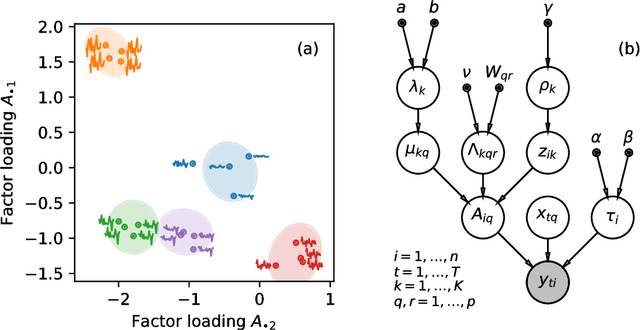
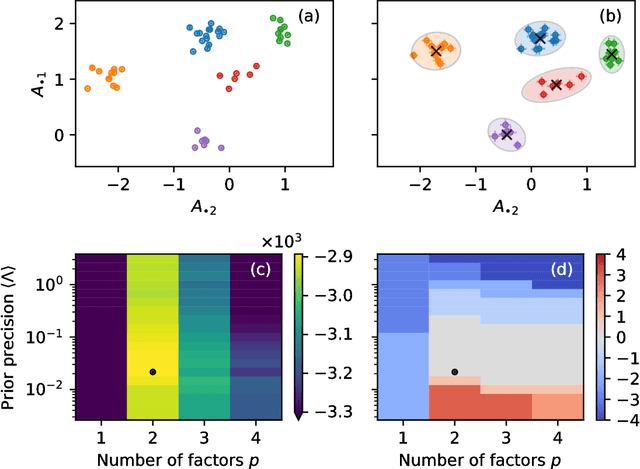
We develop a Bayesian hierarchical model to identify communities in networks for which we do not observe the edges directly, but instead observe a series of interdependent signals for each of the nodes. Fitting the model provides an end-to-end community detection algorithm that does not extract information as a sequence of point estimates but propagates uncertainties from the raw data to the community labels. Our approach naturally supports multiscale community detection as well as the selection of an optimal scale using model comparison. We study the properties of the algorithm using synthetic data and apply it to daily returns of constituents of the S&P100 index as well as climate data from US cities.

The ground truth about metadata and community detection in networks

Across many scientific domains, there is a common need to automatically extract a simplified view or coarse-graining of how a complex system's components interact. This general task is called community detection in networks and is analogous to searching for clusters in independent vector data. It is common to evaluate the performance of community detection algorithms by their ability to find so-called "ground truth" communities. This works well in synthetic networks with planted communities because such networks' links are formed explicitly based on those known communities. However, there are no planted communities in real world networks. Instead, it is standard practice to treat some observed discrete-valued node attributes, or metadata, as ground truth. Here, we show that metadata are not the same as ground truth, and that treating them as such induces severe theoretical and practical problems. We prove that no algorithm can uniquely solve community detection, and we prove a general No Free Lunch theorem for community detection, which implies that there can be no algorithm that is optimal for all possible community detection tasks. However, community detection remains a powerful tool and node metadata still have value so a careful exploration of their relationship with network structure can yield insights of genuine worth. We illustrate this point by introducing two statistical techniques that can quantify the relationship between metadata and community structure for a broad class of models. We demonstrate these techniques using both synthetic and real-world networks, and for multiple types of metadata and community structure.

Graph-based semi-supervised learning for relational networks

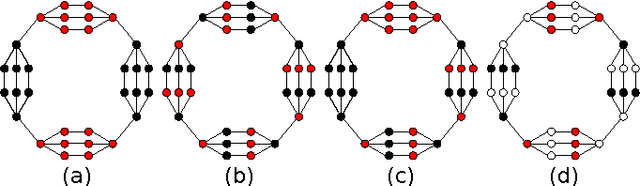
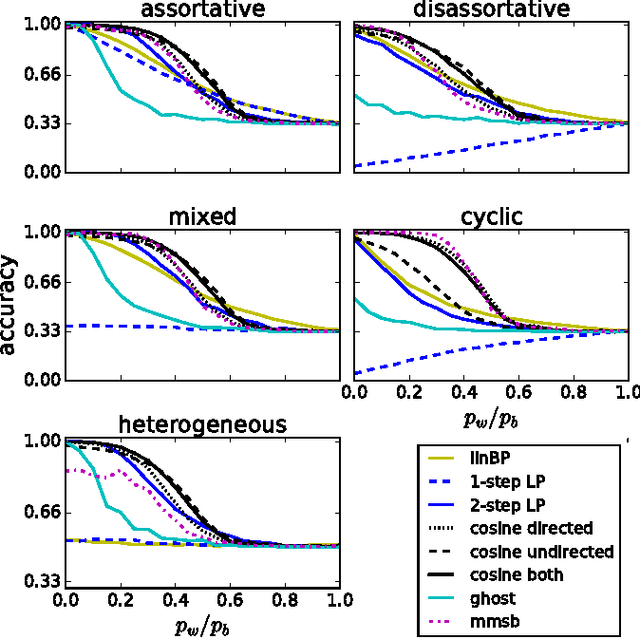
We address the problem of semi-supervised learning in relational networks, networks in which nodes are entities and links are the relationships or interactions between them. Typically this problem is confounded with the problem of graph-based semi-supervised learning (GSSL), because both problems represent the data as a graph and predict the missing class labels of nodes. However, not all graphs are created equally. In GSSL a graph is constructed, often from independent data, based on similarity. As such, edges tend to connect instances with the same class label. Relational networks, however, can be more heterogeneous and edges do not always indicate similarity. For instance, instead of links being more likely to connect nodes with the same class label, they may occur more frequently between nodes with different class labels (link-heterogeneity). Or nodes with the same class label do not necessarily have the same type of connectivity across the whole network (class-heterogeneity), e.g. in a network of sexual interactions we may observe links between opposite genders in some parts of the graph and links between the same genders in others. Performing classification in networks with different types of heterogeneity is a hard problem that is made harder still when we do not know a-priori the type or level of heterogeneity. Here we present two scalable approaches for graph-based semi-supervised learning for the more general case of relational networks. We demonstrate these approaches on synthetic and real-world networks that display different link patterns within and between classes. Compared to state-of-the-art approaches, ours give better classification performance without prior knowledge of how classes interact. In particular, our two-step label propagation algorithm gives consistently good accuracy and runs on networks of over 1.6 million nodes and 30 million edges in around 12 seconds.

Detectability thresholds and optimal algorithms for community structure in dynamic networks

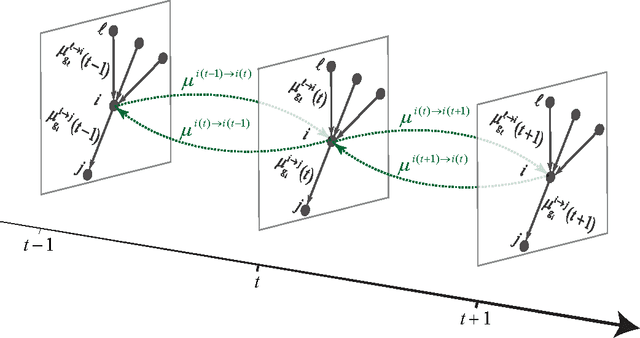
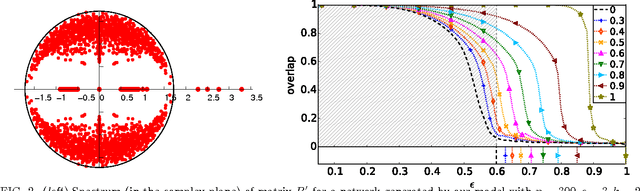
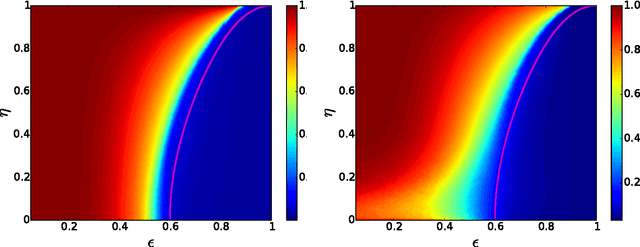
We study the fundamental limits on learning latent community structure in dynamic networks. Specifically, we study dynamic stochastic block models where nodes change their community membership over time, but where edges are generated independently at each time step. In this setting (which is a special case of several existing models), we are able to derive the detectability threshold exactly, as a function of the rate of change and the strength of the communities. Below this threshold, we claim that no algorithm can identify the communities better than chance. We then give two algorithms that are optimal in the sense that they succeed all the way down to this limit. The first uses belief propagation (BP), which gives asymptotically optimal accuracy, and the second is a fast spectral clustering algorithm, based on linearizing the BP equations. We verify our analytic and algorithmic results via numerical simulation, and close with a brief discussion of extensions and open questions.

Detecting change points in the large-scale structure of evolving networks

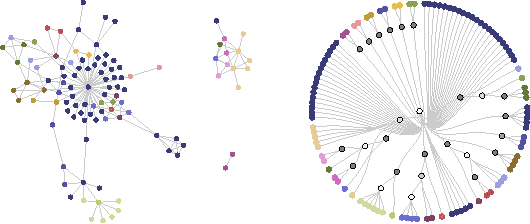
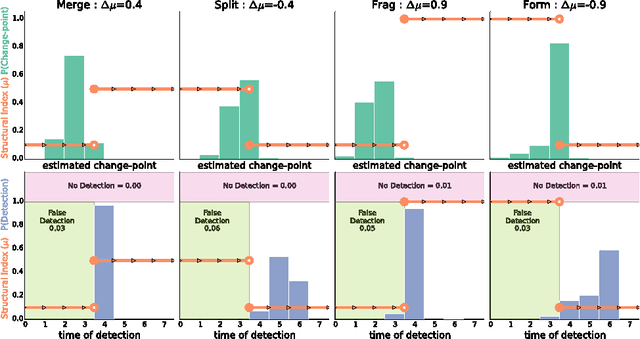
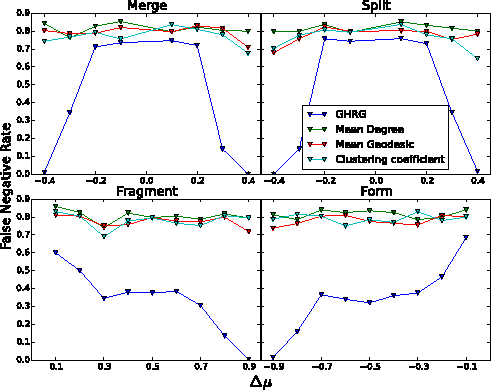
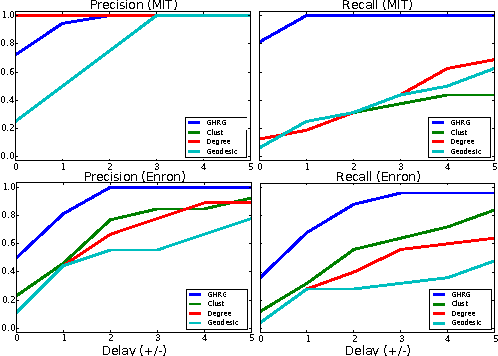
Interactions among people or objects are often dynamic in nature and can be represented as a sequence of networks, each providing a snapshot of the interactions over a brief period of time. An important task in analyzing such evolving networks is change-point detection, in which we both identify the times at which the large-scale pattern of interactions changes fundamentally and quantify how large and what kind of change occurred. Here, we formalize for the first time the network change-point detection problem within an online probabilistic learning framework and introduce a method that can reliably solve it. This method combines a generalized hierarchical random graph model with a Bayesian hypothesis test to quantitatively determine if, when, and precisely how a change point has occurred. We analyze the detectability of our method using synthetic data with known change points of different types and magnitudes, and show that this method is more accurate than several previously used alternatives. Applied to two high-resolution evolving social networks, this method identifies a sequence of change points that align with known external "shocks" to these networks.

Active Discovery of Network Roles for Predicting the Classes of Network Nodes

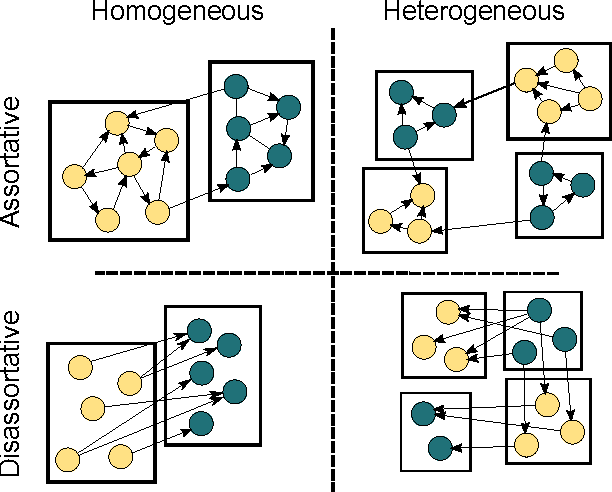
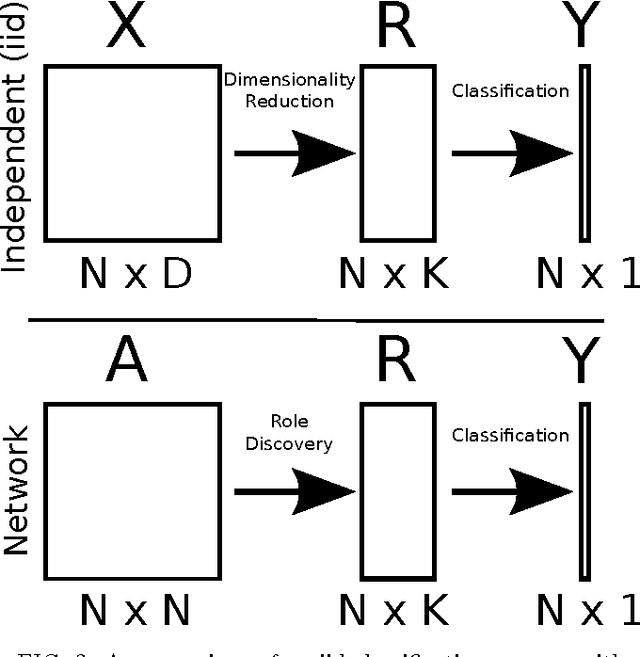
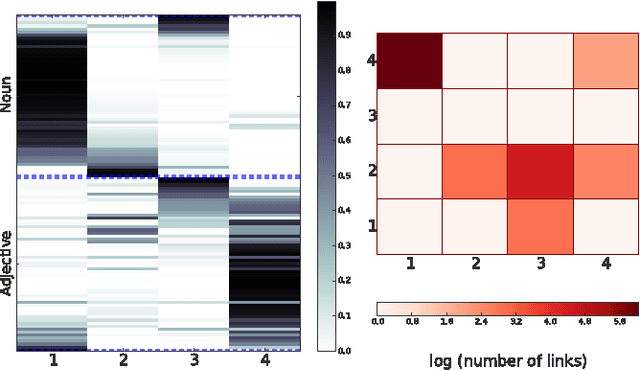
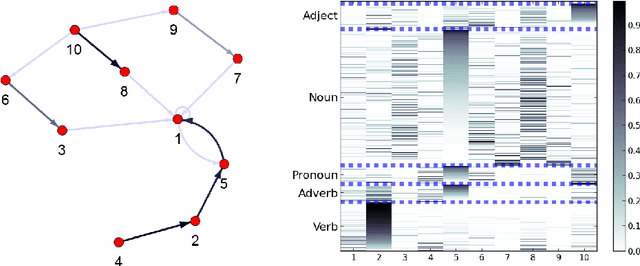
Nodes in real world networks often have class labels, or underlying attributes, that are related to the way in which they connect to other nodes. Sometimes this relationship is simple, for instance nodes of the same class are may be more likely to be connected. In other cases, however, this is not true, and the way that nodes link in a network exhibits a different, more complex relationship to their attributes. Here, we consider networks in which we know how the nodes are connected, but we do not know the class labels of the nodes or how class labels relate to the network links. We wish to identify the best subset of nodes to label in order to learn this relationship between node attributes and network links. We can then use this discovered relationship to accurately predict the class labels of the rest of the network nodes. We present a model that identifies groups of nodes with similar link patterns, which we call network roles, using a generative blockmodel. The model then predicts labels by learning the mapping from network roles to class labels using a maximum margin classifier. We choose a subset of nodes to label according to an iterative margin-based active learning strategy. By integrating the discovery of network roles with the classifier optimisation, the active learning process can adapt the network roles to better represent the network for node classification. We demonstrate the model by exploring a selection of real world networks, including a marine food web and a network of English words. We show that, in contrast to other network classifiers, this model achieves good classification accuracy for a range of networks with different relationships between class labels and network links.

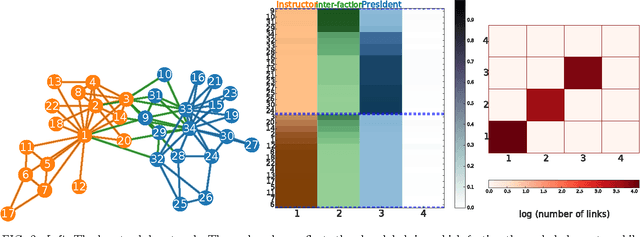
Supervised Blockmodelling

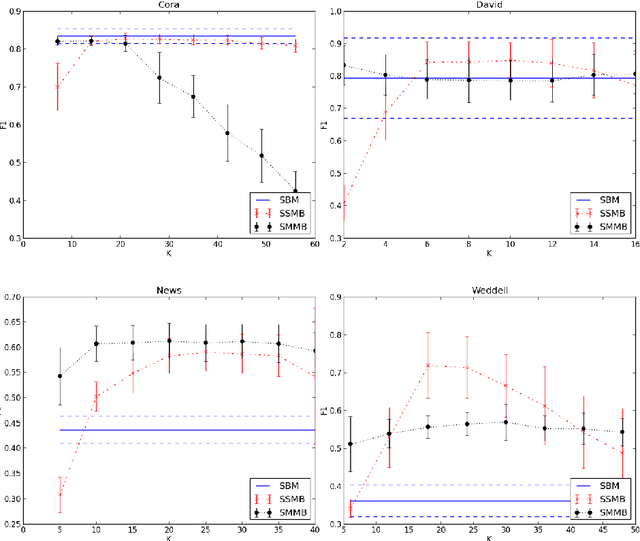
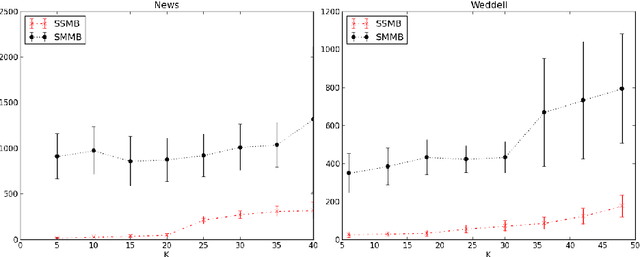
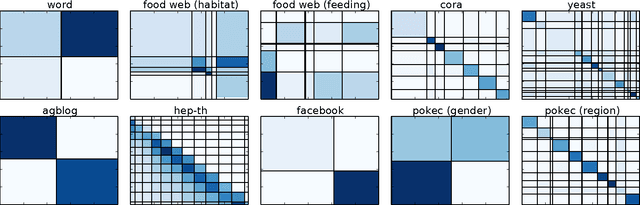
Collective classification models attempt to improve classification performance by taking into account the class labels of related instances. However, they tend not to learn patterns of interactions between classes and/or make the assumption that instances of the same class link to each other (assortativity assumption). Blockmodels provide a solution to these issues, being capable of modelling assortative and disassortative interactions, and learning the pattern of interactions in the form of a summary network. The Supervised Blockmodel provides good classification performance using link structure alone, whilst simultaneously providing an interpretable summary of network interactions to allow a better understanding of the data. This work explores three variants of supervised blockmodels of varying complexity and tests them on four structurally different real world networks.