Matrix-weighted networks for modeling multidimensional dynamics

Networks are powerful tools for modeling interactions in complex systems. While traditional networks use scalar edge weights, many real-world systems involve multidimensional interactions. For example, in social networks, individuals often have multiple interconnected opinions that can affect different opinions of other individuals, which can be better characterized by matrices. We propose a novel, general framework for modeling such multidimensional interacting dynamics: matrix-weighted networks (MWNs). We present the mathematical foundations of MWNs and examine consensus dynamics and random walks within this context. Our results reveal that the coherence of MWNs gives rise to non-trivial steady states that generalize the notions of communities and structural balance in traditional networks.

Strong and Weak Random Walks on Signed Networks

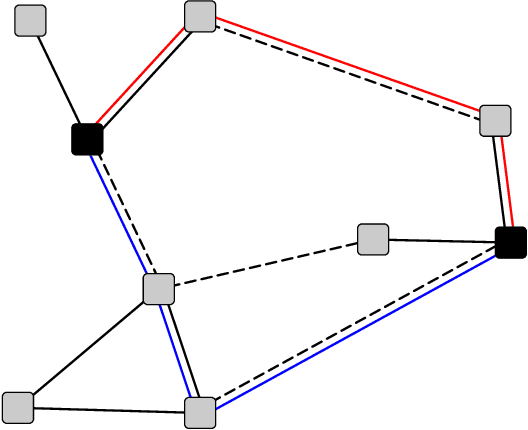
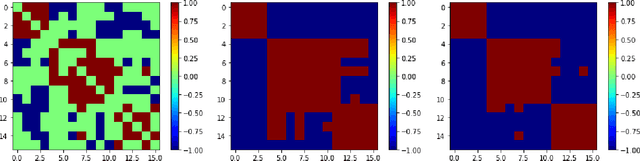
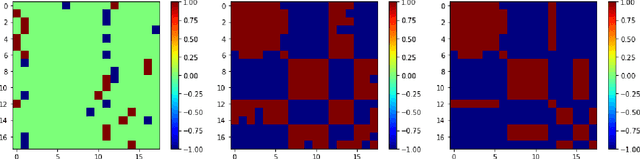
Random walks play an important role in probing the structure of complex networks. On traditional networks, they can be used to extract community structure, understand node centrality, perform link prediction, or capture the similarity between nodes. On signed networks, where the edge weights can be either positive or negative, it is non-trivial to design a random walk which can be used to extract information about the signed structure of the network, in particular the ability to partition the graph into communities with positive edges inside and negative edges in between. Prior works on signed network random walks focus on the case where there are only two such communities (strong balance), which is rarely the case in empirical networks. In this paper, we propose a signed network random walk which can capture the structure of a network with more than two such communities (weak balance). The walk results in a similarity matrix which can be used to cluster the nodes into antagonistic communities. We compare the characteristics of the so-called strong and weak random walks, in terms of walk length and stationarity. We show through a series of experiments on synthetic and empirical networks that the similarity matrix based on weak walks can be used for both unsupervised and semi-supervised clustering, outperforming the same similarity matrix based on strong walks when the graph has more than two communities, or exhibits asymmetry in the density of links. These results suggest that other random-walk based algorithms for signed networks could be improved simply by running them with weak walks instead of strong walks.

Link Me Baby One More Time: Social Music Discovery on Spotify

We explore the social and contextual factors that influence the outcome of person-to-person music recommendations and discovery. Specifically, we use data from Spotify to investigate how a link sent from one user to another results in the receiver engaging with the music of the shared artist. We consider several factors that may influence this process, such as the strength of the sender-receiver relationship, the user's role in the Spotify social network, their music social cohesion, and how similar the new artist is to the receiver's taste. We find that the receiver of a link is more likely to engage with a new artist when (1) they have similar music taste to the sender and the shared track is a good fit for their taste, (2) they have a stronger and more intimate tie with the sender, and (3) the shared artist is popular with the receiver's connections. Finally, we use these findings to build a Random Forest classifier to predict whether a shared music track will result in the receiver's engagement with the shared artist. This model elucidates which type of social and contextual features are most predictive, although peak performance is achieved when a diverse set of features are included. These findings provide new insights into the multifaceted mechanisms underpinning the interplay between music discovery and social processes.

Structural Balance and Random Walks on Complex Networks with Complex Weights

Complex numbers define the relationship between entities in many situations. A canonical example would be the off-diagonal terms in a Hamiltonian matrix in quantum physics. Recent years have seen an increasing interest to extend the tools of network science when the weight of edges are complex numbers. Here, we focus on the case when the weight matrix is Hermitian, a reasonable assumption in many applications, and investigate both structural and dynamical properties of the complex-weighted networks. Building on concepts from signed graphs, we introduce a classification of complex-weighted networks based on the notion of structural balance, and illustrate the shared spectral properties within each type. We then apply the results to characterise the dynamics of random walks on complex-weighted networks, where local consensus can be achieved asymptotically when the graph is structurally balanced, while global consensus will be obtained when it is strictly unbalanced. Finally, we explore potential applications of our findings by generalising the notion of cut, and propose an associated spectral clustering algorithm. We also provide further characteristics of the magnetic Laplacian, associating directed networks to complex-weighted ones. The performance of the algorithm is verified on both synthetic and real networks.

Exploring QSAR Models for Activity-Cliff Prediction

Pairs of similar compounds that only differ by a small structural modification but exhibit a large difference in their binding affinity for a given target are known as activity cliffs (ACs). It has been hypothesised that quantitative structure-activity relationship (QSAR) models struggle to predict ACs and that ACs thus form a major source of prediction error. However, a study to explore the AC-prediction power of modern QSAR methods and its relationship to general QSAR-prediction performance is lacking. We systematically construct nine distinct QSAR models by combining three molecular representation methods (extended-connectivity fingerprints, physicochemical-descriptor vectors and graph isomorphism networks) with three regression techniques (random forests, k-nearest neighbours and multilayer perceptrons); we then use each resulting model to classify pairs of similar compounds as ACs or non-ACs and to predict the activities of individual molecules in three case studies: dopamine receptor D2, factor Xa, and SARS-CoV-2 main protease. We observe low AC-sensitivity amongst the tested models when the activities of both compounds are unknown, but a substantial increase in AC-sensitivity when the actual activity of one of the compounds is given. Graph isomorphism features are found to be competitive with or superior to classical molecular representations for AC-classification and can thus be employed as baseline AC-prediction models or simple compound-optimisation tools. For general QSAR-prediction, however, extended-connectivity fingerprints still consistently deliver the best performance. Our results provide strong support for the hypothesis that indeed QSAR methods frequently fail to predict ACs. We propose twin-network training for deep learning models as a potential future pathway to increase AC-sensitivity and thus overall QSAR performance.

Community detection in networks with unobserved edges

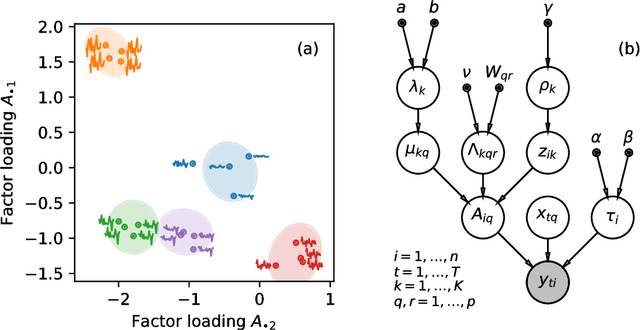
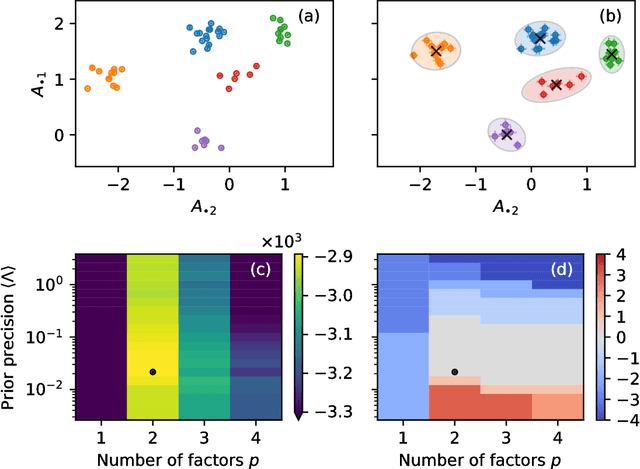
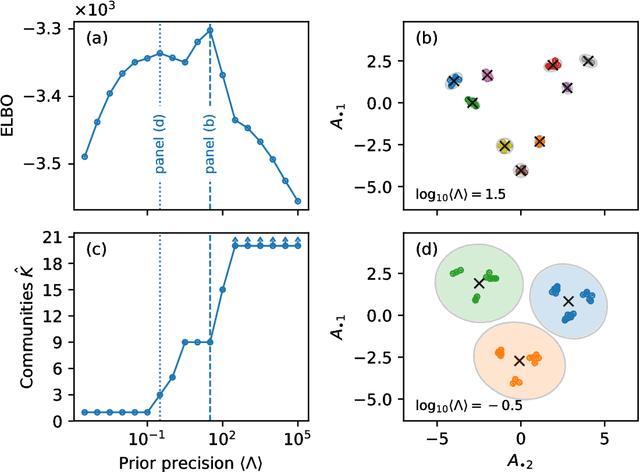
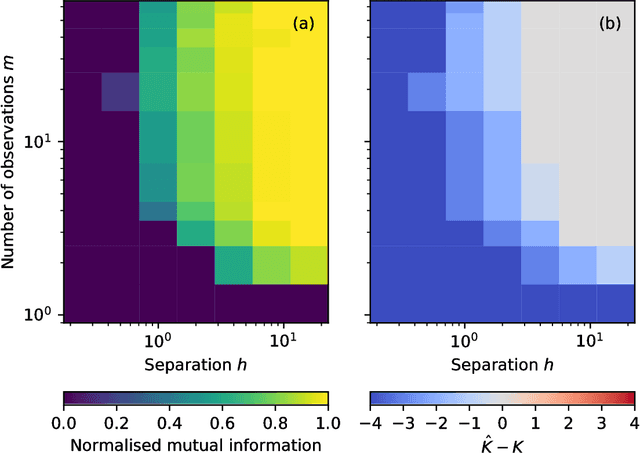
We develop a Bayesian hierarchical model to identify communities in networks for which we do not observe the edges directly, but instead observe a series of interdependent signals for each of the nodes. Fitting the model provides an end-to-end community detection algorithm that does not extract information as a sequence of point estimates but propagates uncertainties from the raw data to the community labels. Our approach naturally supports multiscale community detection as well as the selection of an optimal scale using model comparison. We study the properties of the algorithm using synthetic data and apply it to daily returns of constituents of the S&P100 index as well as climate data from US cities.

RankMerging: A supervised learning-to-rank framework to predict links in large social network

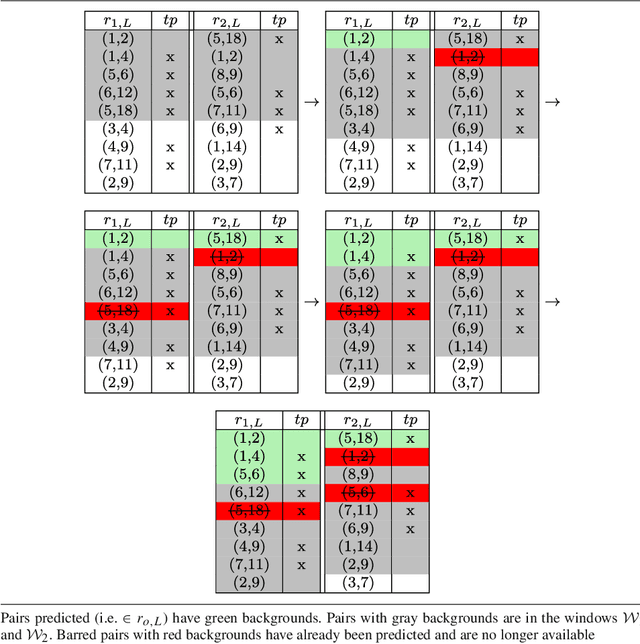
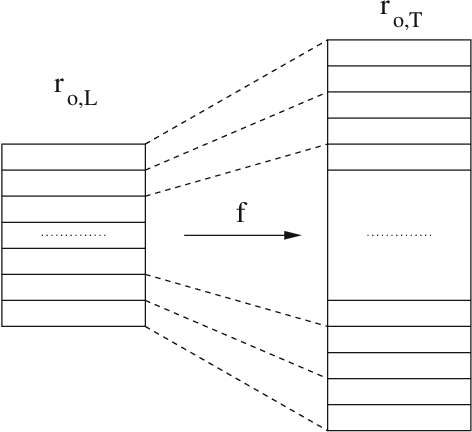
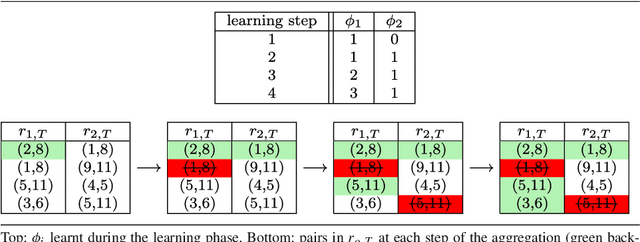
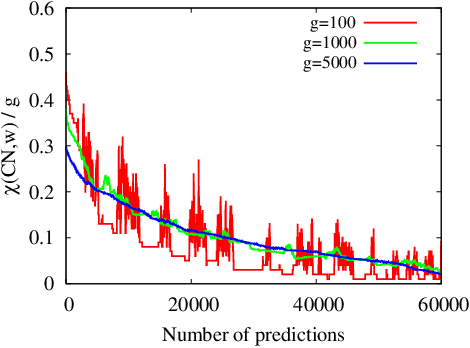
Uncovering unknown or missing links in social networks is a difficult task because of their sparsity and because links may represent different types of relationships, characterized by different structural patterns. In this paper, we define a simple yet efficient supervised learning-to-rank framework, called RankMerging, which aims at combining information provided by various unsupervised rankings. We illustrate our method on three different kinds of social networks and show that it substantially improves the performances of unsupervised metrics of ranking. We also compare it to other combination strategies based on standard methods. Finally, we explore various aspects of RankMerging, such as feature selection and parameter estimation and discuss its area of relevance: the prediction of an adjustable number of links on large networks.