Geodesic statistics for random network families

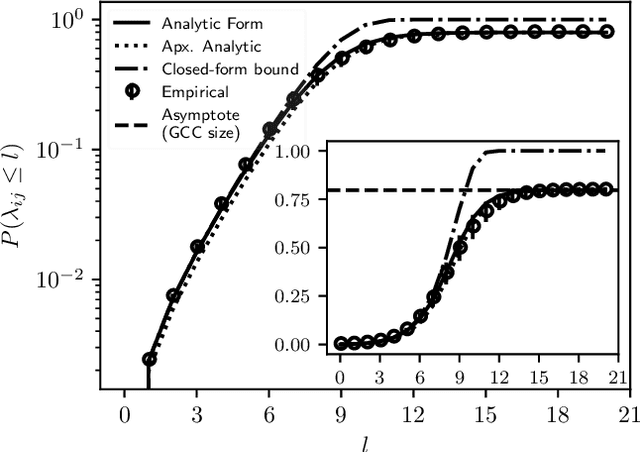
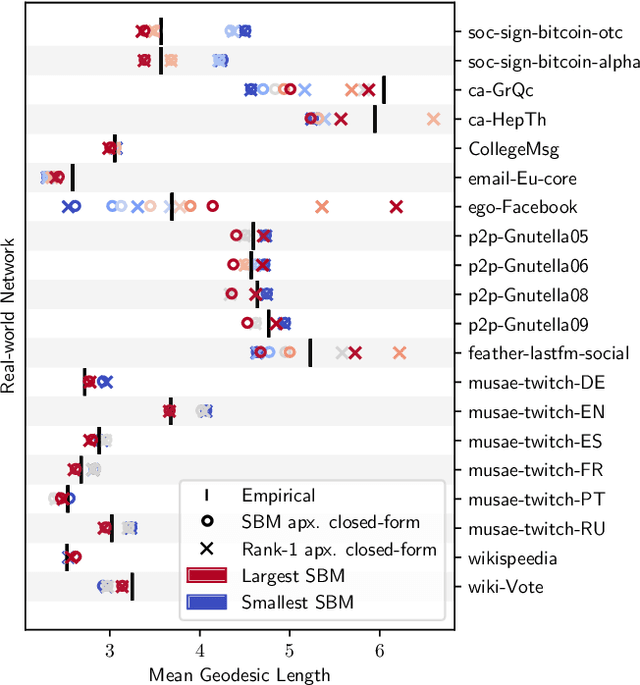
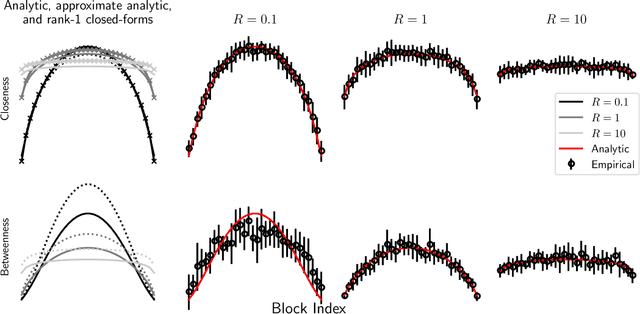
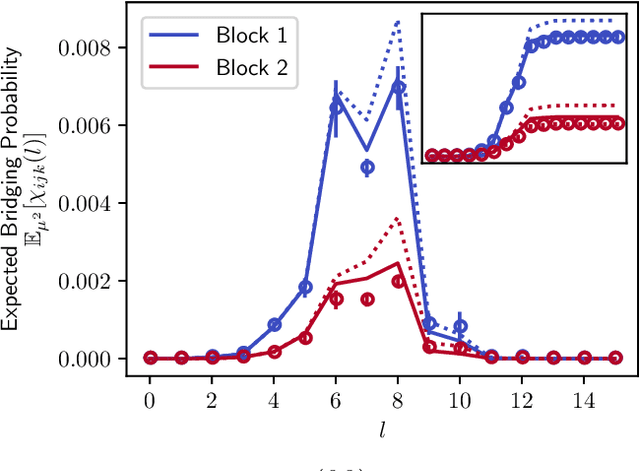
A key task in the study of networked systems is to derive local and global properties that impact connectivity, synchronizability, and robustness. Computing shortest paths or geodesics in the network yields measures of node centrality and network connectivity that can contribute to explain such phenomena. We derive an analytic distribution of shortest path lengths, on the giant component in the supercritical regime or on small components in the subcritical regime, of any sparse (possibly directed) graph with conditionally independent edges, in the infinite-size limit. We provide specific results for widely used network families like stochastic block models, dot-product graphs, random geometric graphs, and graphons. The survival function of the shortest path length distribution possesses a simple closed-form lower bound which is asymptotically tight for finite lengths, has a natural interpretation of traversing independent geodesics in the network, and delivers novel insight in the above network families. Notably, the shortest path length distribution allows us to derive, for the network families above, important graph properties like the bond percolation threshold, size of the giant component, average shortest path length, and closeness and betweenness centralities. We also provide a corroborative analysis of a set of 20 empirical networks. This unifying framework demonstrates how geodesic statistics for a rich family of random graphs can be computed cheaply without having access to true or simulated networks, especially when they are sparse but prohibitively large.

Modularity maximisation for graphons

Networks are a widely-used tool to investigate the large-scale connectivity structure in complex systems and graphons have been proposed as an infinite size limit of dense networks. The detection of communities or other meso-scale structures is a prominent topic in network science as it allows the identification of functional building blocks in complex systems. When such building blocks may be present in graphons is an open question. In this paper, we define a graphon-modularity and demonstrate that it can be maximised to detect communities in graphons. We then investigate specific synthetic graphons and show that they may show a wide range of different community structures. We also reformulate the graphon-modularity maximisation as a continuous optimisation problem and so prove the optimal community structure or lack thereof for some graphons, something that is usually not possible for networks. Furthermore, we demonstrate that estimating a graphon from network data as an intermediate step can improve the detection of communities, in comparison with exclusively maximising the modularity of the network. While the choice of graphon-estimator may strongly influence the accord between the community structure of a network and its estimated graphon, we find that there is a substantial overlap if an appropriate estimator is used. Our study demonstrates that community detection for graphons is possible and may serve as a privacy-preserving way to cluster network data.

Community detection in networks with unobserved edges

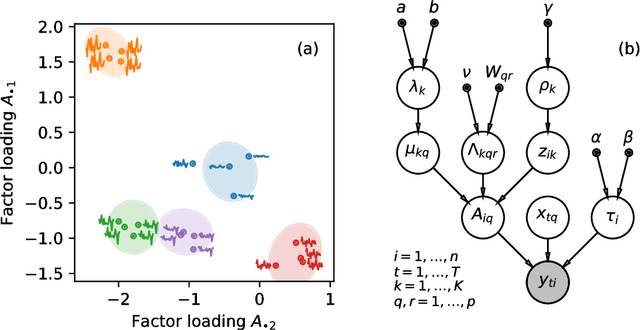
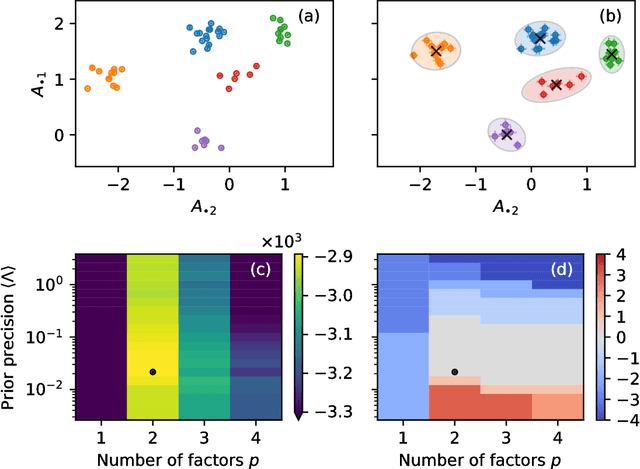
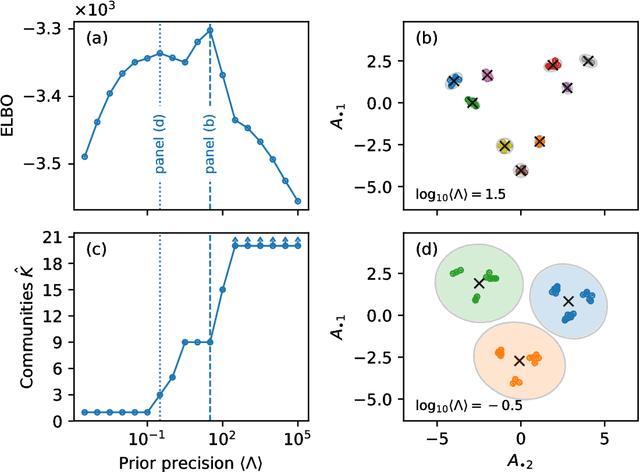
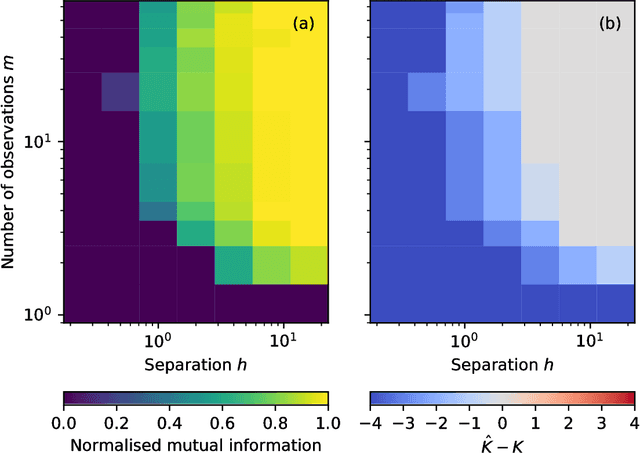
We develop a Bayesian hierarchical model to identify communities in networks for which we do not observe the edges directly, but instead observe a series of interdependent signals for each of the nodes. Fitting the model provides an end-to-end community detection algorithm that does not extract information as a sequence of point estimates but propagates uncertainties from the raw data to the community labels. Our approach naturally supports multiscale community detection as well as the selection of an optimal scale using model comparison. We study the properties of the algorithm using synthetic data and apply it to daily returns of constituents of the S&P100 index as well as climate data from US cities.

Highly comparative fetal heart rate analysis

A database of fetal heart rate (FHR) time series measured from 7221 patients during labor is analyzed with the aim of learning the types of features of these recordings that are informative of low cord pH. Our 'highly comparative' analysis involves extracting over 9000 time-series analysis features from each FHR time series, including measures of autocorrelation, entropy, distribution, and various model fits. This diverse collection of features was developed in previous work, and is publicly available. We describe five features that most accurately classify a balanced training set of 59 'low pH' and 59 'normal pH' FHR recordings. We then describe five of the features with the strongest linear correlation to cord pH across the full dataset of FHR time series. The features identified in this work may be used as part of a system for guiding intervention during labor in future. This work successfully demonstrates the utility of comparing across a large, interdisciplinary literature on time-series analysis to automatically contribute new scientific results for specific biomedical signal processing challenges.

Highly comparative feature-based time-series classification

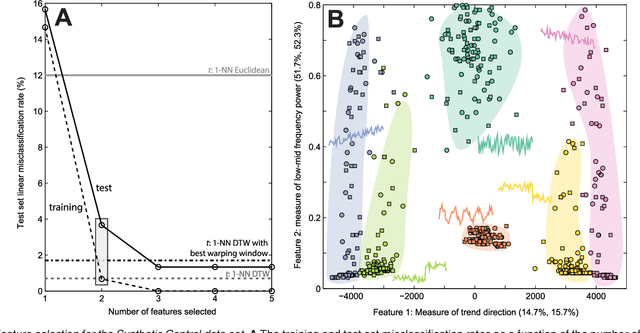
A highly comparative, feature-based approach to time series classification is introduced that uses an extensive database of algorithms to extract thousands of interpretable features from time series. These features are derived from across the scientific time-series analysis literature, and include summaries of time series in terms of their correlation structure, distribution, entropy, stationarity, scaling properties, and fits to a range of time-series models. After computing thousands of features for each time series in a training set, those that are most informative of the class structure are selected using greedy forward feature selection with a linear classifier. The resulting feature-based classifiers automatically learn the differences between classes using a reduced number of time-series properties, and circumvent the need to calculate distances between time series. Representing time series in this way results in orders of magnitude of dimensionality reduction, allowing the method to perform well on very large datasets containing long time series or time series of different lengths. For many of the datasets studied, classification performance exceeded that of conventional instance-based classifiers, including one nearest neighbor classifiers using Euclidean distances and dynamic time warping and, most importantly, the features selected provide an understanding of the properties of the dataset, insight that can guide further scientific investigation.

Highly comparative time-series analysis: The empirical structure of time series and their methods

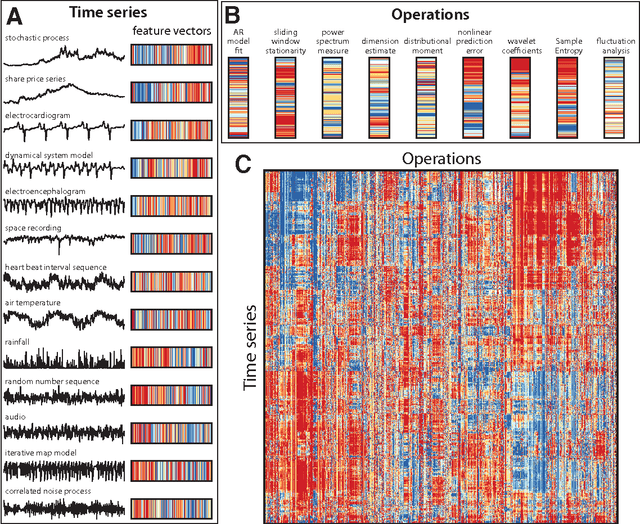
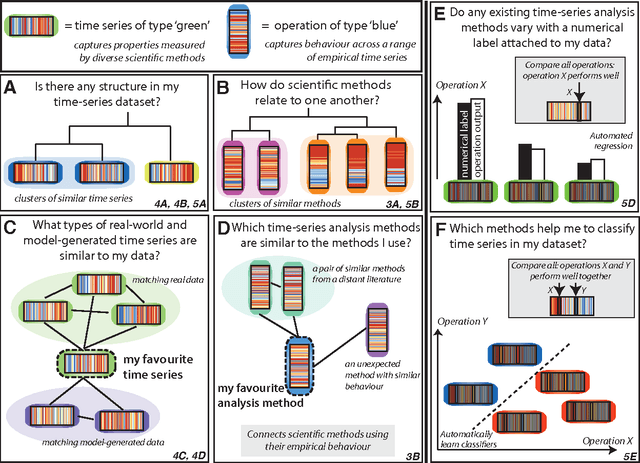
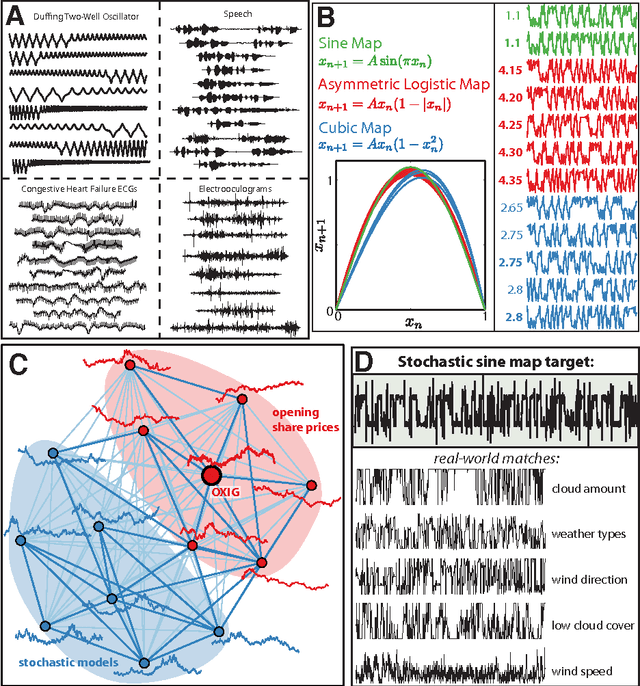
The process of collecting and organizing sets of observations represents a common theme throughout the history of science. However, despite the ubiquity of scientists measuring, recording, and analyzing the dynamics of different processes, an extensive organization of scientific time-series data and analysis methods has never been performed. Addressing this, annotated collections of over 35 000 real-world and model-generated time series and over 9000 time-series analysis algorithms are analyzed in this work. We introduce reduced representations of both time series, in terms of their properties measured by diverse scientific methods, and of time-series analysis methods, in terms of their behaviour on empirical time series, and use them to organize these interdisciplinary resources. This new approach to comparing across diverse scientific data and methods allows us to organize time-series datasets automatically according to their properties, retrieve alternatives to particular analysis methods developed in other scientific disciplines, and automate the selection of useful methods for time-series classification and regression tasks. The broad scientific utility of these tools is demonstrated on datasets of electroencephalograms, self-affine time series, heart beat intervals, speech signals, and others, in each case contributing novel analysis techniques to the existing literature. Highly comparative techniques that compare across an interdisciplinary literature can thus be used to guide more focused research in time-series analysis for applications across the scientific disciplines.

Evolutionary Inference for Function-valued Traits: Gaussian Process Regression on Phylogenies

Biological data objects often have both of the following features: (i) they are functions rather than single numbers or vectors, and (ii) they are correlated due to phylogenetic relationships. In this paper we give a flexible statistical model for such data, by combining assumptions from phylogenetics with Gaussian processes. We describe its use as a nonparametric Bayesian prior distribution, both for prediction (placing posterior distributions on ancestral functions) and model selection (comparing rates of evolution across a phylogeny, or identifying the most likely phylogenies consistent with the observed data). Our work is integrative, extending the popular phylogenetic Brownian Motion and Ornstein-Uhlenbeck models to functional data and Bayesian inference, and extending Gaussian Process regression to phylogenies. We provide a brief illustration of the application of our method.

Ancestral Inference from Functional Data: Statistical Methods and Numerical Examples

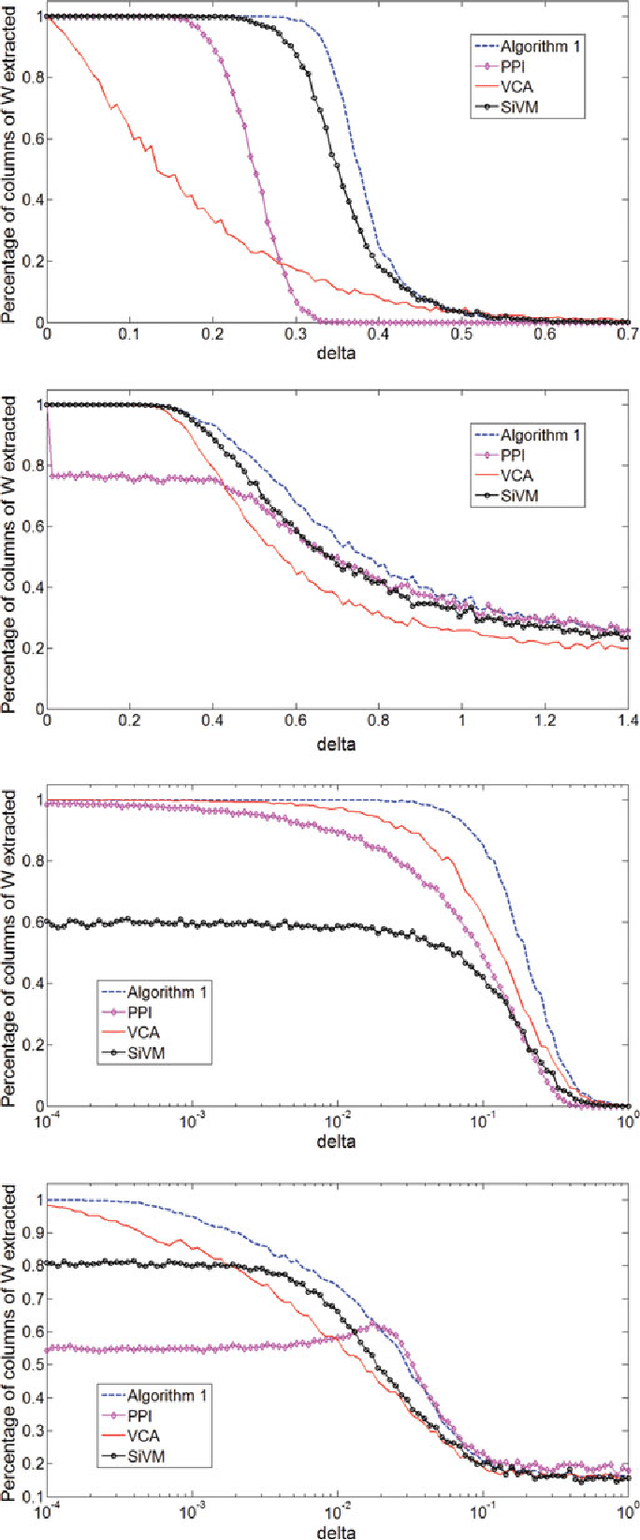
Many biological characteristics of evolutionary interest are not scalar variables but continuous functions. Here we use phylogenetic Gaussian process regression to model the evolution of simulated function-valued traits. Given function-valued data only from the tips of an evolutionary tree and utilising independent principal component analysis (IPCA) as a method for dimension reduction, we construct distributional estimates of ancestral function-valued traits, and estimate parameters describing their evolutionary dynamics.