RangL: A Reinforcement Learning Competition Platform

The RangL project hosted by The Alan Turing Institute aims to encourage the wider uptake of reinforcement learning by supporting competitions relating to real-world dynamic decision problems. This article describes the reusable code repository developed by the RangL team and deployed for the 2022 Pathways to Net Zero Challenge, supported by the UK Net Zero Technology Centre. The winning solutions to this particular Challenge seek to optimize the UK's energy transition policy to net zero carbon emissions by 2050. The RangL repository includes an OpenAI Gym reinforcement learning environment and code that supports both submission to, and evaluation in, a remote instance of the open source EvalAI platform as well as all winning learning agent strategies. The repository is an illustrative example of RangL's capability to provide a reusable structure for future challenges.

Evolutionary Inference for Function-valued Traits: Gaussian Process Regression on Phylogenies

Biological data objects often have both of the following features: (i) they are functions rather than single numbers or vectors, and (ii) they are correlated due to phylogenetic relationships. In this paper we give a flexible statistical model for such data, by combining assumptions from phylogenetics with Gaussian processes. We describe its use as a nonparametric Bayesian prior distribution, both for prediction (placing posterior distributions on ancestral functions) and model selection (comparing rates of evolution across a phylogeny, or identifying the most likely phylogenies consistent with the observed data). Our work is integrative, extending the popular phylogenetic Brownian Motion and Ornstein-Uhlenbeck models to functional data and Bayesian inference, and extending Gaussian Process regression to phylogenies. We provide a brief illustration of the application of our method.

Ancestral Inference from Functional Data: Statistical Methods and Numerical Examples

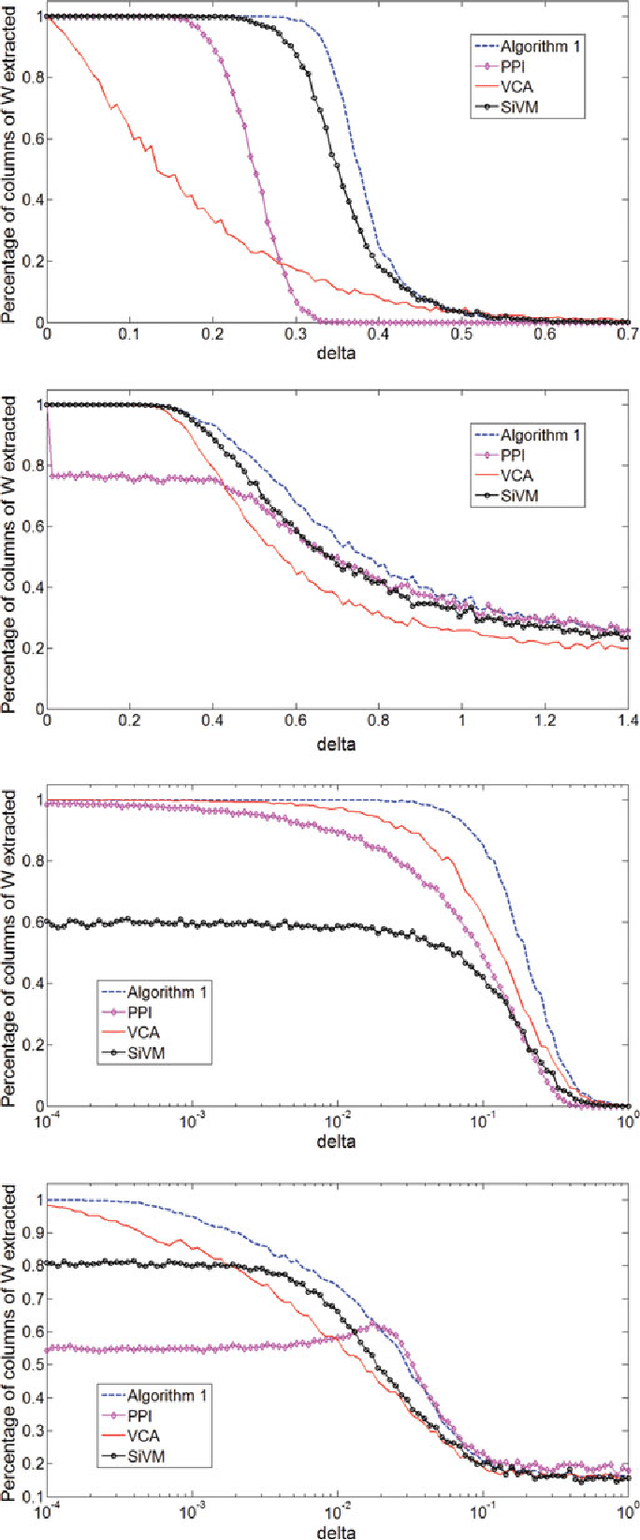
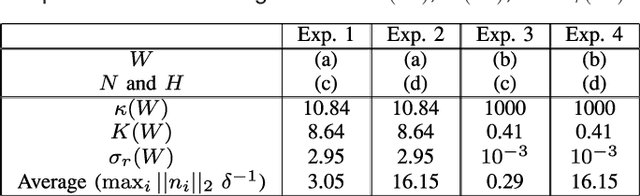
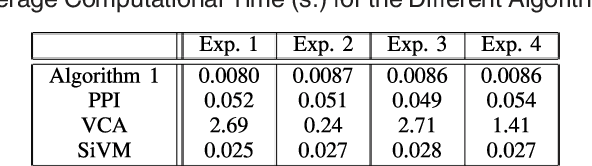
Many biological characteristics of evolutionary interest are not scalar variables but continuous functions. Here we use phylogenetic Gaussian process regression to model the evolution of simulated function-valued traits. Given function-valued data only from the tips of an evolutionary tree and utilising independent principal component analysis (IPCA) as a method for dimension reduction, we construct distributional estimates of ancestral function-valued traits, and estimate parameters describing their evolutionary dynamics.