Parameter inference from a non-stationary unknown process

Non-stationary systems are found throughout the world, from climate patterns under the influence of variation in carbon dioxide concentration, to brain dynamics driven by ascending neuromodulation. Accordingly, there is a need for methods to analyze non-stationary processes, and yet most time-series analysis methods that are used in practice, on important problems across science and industry, make the simplifying assumption of stationarity. One important problem in the analysis of non-stationary systems is the problem class that we refer to as Parameter Inference from a Non-stationary Unknown Process (PINUP). Given an observed time series, this involves inferring the parameters that drive non-stationarity of the time series, without requiring knowledge or inference of a mathematical model of the underlying system. Here we review and unify a diverse literature of algorithms for PINUP. We formulate the problem, and categorize the various algorithmic contributions. This synthesis will allow researchers to identify gaps in the literature and will enable systematic comparisons of different methods. We also demonstrate that the most common systems that existing methods are tested on - notably the non-stationary Lorenz process and logistic map - are surprisingly easy to perform well on using simple statistical features like windowed mean and variance, undermining the practice of using good performance on these systems as evidence of algorithmic performance. We then identify more challenging problems that many existing methods perform poorly on and which can be used to drive methodological advances in the field. Our results unify disjoint scientific contributions to analyzing non-stationary systems and suggest new directions for progress on the PINUP problem and the broader study of non-stationary phenomena.

Never a Dull Moment: Distributional Properties as a Baseline for Time-Series Classification

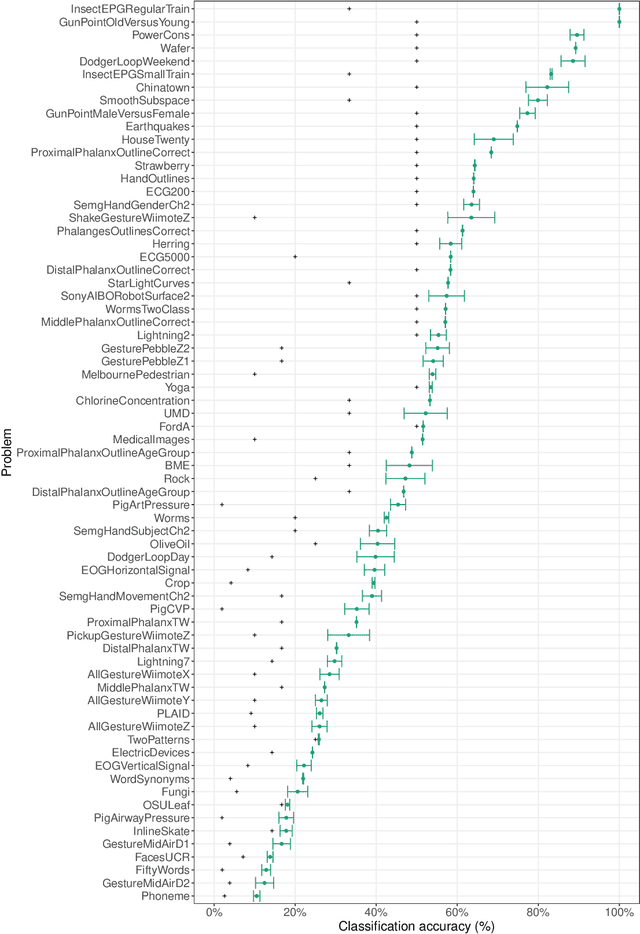
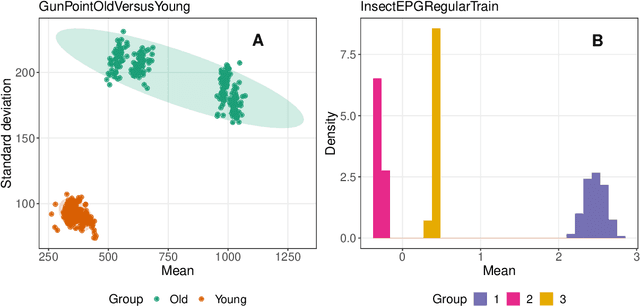
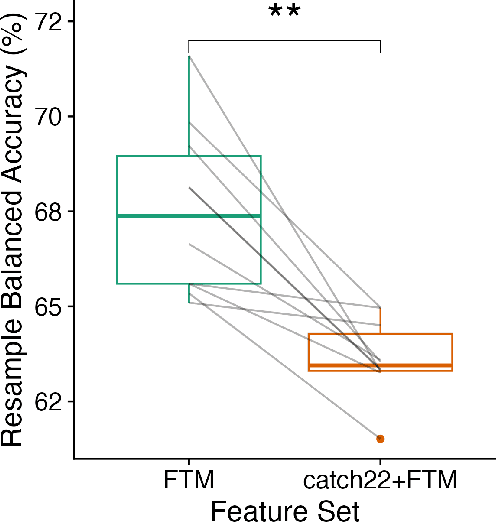
The variety of complex algorithmic approaches for tackling time-series classification problems has grown considerably over the past decades, including the development of sophisticated but challenging-to-interpret deep-learning-based methods. But without comparison to simpler methods it can be difficult to determine when such complexity is required to obtain strong performance on a given problem. Here we evaluate the performance of an extremely simple classification approach -- a linear classifier in the space of two simple features that ignore the sequential ordering of the data: the mean and standard deviation of time-series values. Across a large repository of 128 univariate time-series classification problems, this simple distributional moment-based approach outperformed chance on 69 problems, and reached 100% accuracy on two problems. With a neuroimaging time-series case study, we find that a simple linear model based on the mean and standard deviation performs better at classifying individuals with schizophrenia than a model that additionally includes features of the time-series dynamics. Comparing the performance of simple distributional features of a time series provides important context for interpreting the performance of complex time-series classification models, which may not always be required to obtain high accuracy.

Feature-Based Time-Series Analysis in R using the theft Package

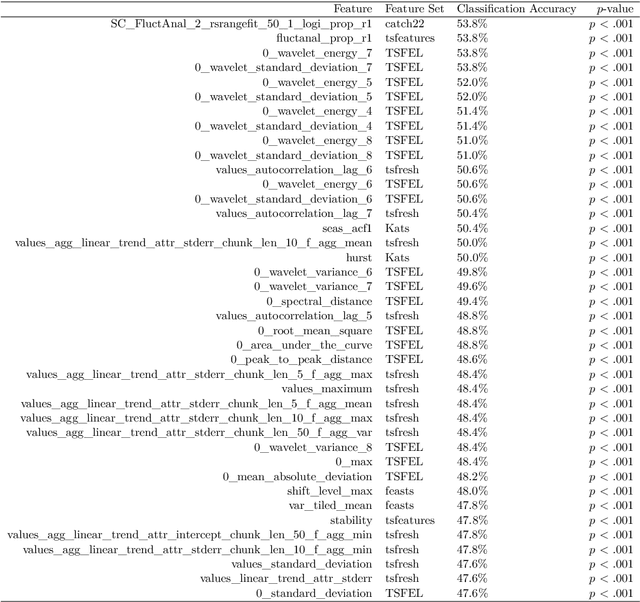
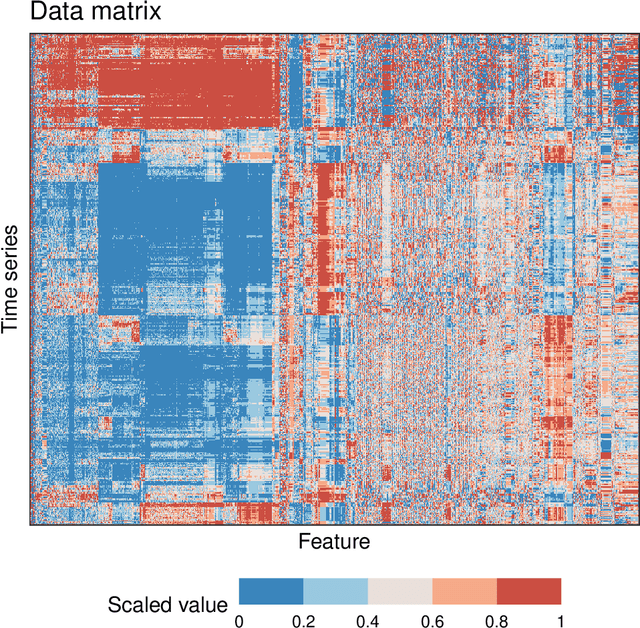
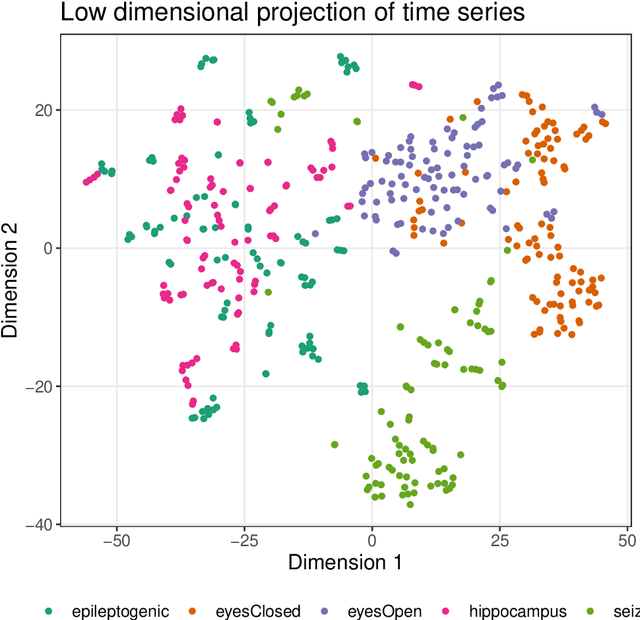
Time series are measured and analyzed across the sciences. One method of quantifying the structure of time series is by calculating a set of summary statistics or `features', and then representing a time series in terms of its properties as a feature vector. The resulting feature space is interpretable and informative, and enables conventional statistical learning approaches, including clustering, regression, and classification, to be applied to time-series datasets. Many open-source software packages for computing sets of time-series features exist across multiple programming languages, including catch22 (22 features: Matlab, R, Python, Julia), feasts (42 features: R), tsfeatures (63 features: R), Kats (40 features: Python), tsfresh (779 features: Python), and TSFEL (390 features: Python). However, there are several issues: (i) a singular access point to these packages is not currently available; (ii) to access all feature sets, users must be fluent in multiple languages; and (iii) these feature-extraction packages lack extensive accompanying methodological pipelines for performing feature-based time-series analysis, such as applications to time-series classification. Here we introduce a solution to these issues in an R software package called theft: Tools for Handling Extraction of Features from Time series. theft is a unified and extendable framework for computing features from the six open-source time-series feature sets listed above. It also includes a suite of functions for processing and interpreting the performance of extracted features, including extensive data-visualization templates, low-dimensional projections, and time-series classification operations. With an increasing volume and complexity of time-series datasets in the sciences and industry, theft provides a standardized framework for comprehensively quantifying and interpreting informative structure in time series.

Unifying Pairwise Interactions in Complex Dynamics

Scientists have developed hundreds of techniques to measure the interactions between pairs of processes in complex systems. But these computational methods -- from correlation coefficients to causal inference -- rely on distinct quantitative theories that remain largely disconnected. Here we introduce a library of 249 statistics for pairwise interactions and assess their behavior on 1053 multivariate time series from a wide range of real-world and model-generated systems. Our analysis highlights new commonalities between different mathematical formulations, providing a unified picture of a rich, interdisciplinary literature. We then show that leveraging many methods from across science can uncover those most suitable for addressing a given problem, yielding high accuracy and interpretable understanding. Our framework is provided in extendable open software, enabling comprehensive data-driven analysis by integrating decades of methodological advances.

An Empirical Evaluation of Time-Series Feature Sets

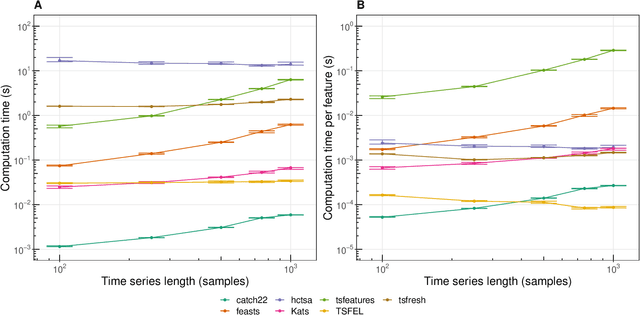
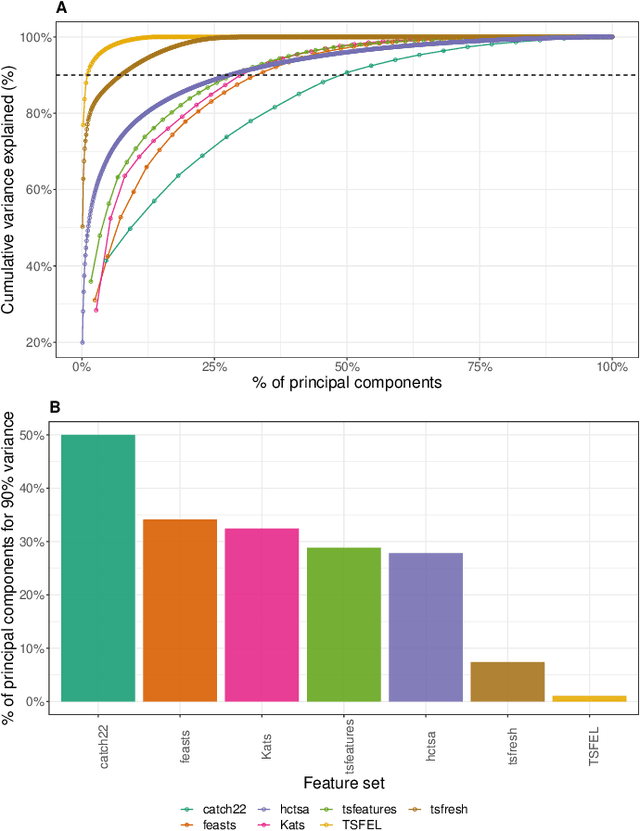
Solving time-series problems with features has been rising in popularity due to the availability of software for feature extraction. Feature-based time-series analysis can now be performed using many different feature sets, including hctsa (7730 features: Matlab), feasts (42 features: R), tsfeatures (63 features: R), Kats (40 features: Python), tsfresh (up to 1558 features: Python), TSFEL (390 features: Python), and the C-coded catch22 (22 features: Matlab, R, Python, and Julia). There is substantial overlap in the types of methods included in these sets (e.g., properties of the autocorrelation function and Fourier power spectrum), but they are yet to be systematically compared. Here we compare these seven sets on computational speed, assess the redundancy of features contained in each, and evaluate the overlap and redundancy between them. We take an empirical approach to feature similarity based on outputs across a diverse set of real-world and simulated time series. We find that feature sets vary across three orders of magnitude in their computation time per feature on a laptop for a 1000-sample series, from the fastest sets catch22 and TSFEL (~0.1ms per feature) to tsfeatures (~3s per feature). Using PCA to evaluate feature redundancy within each set, we find the highest within-set redundancy for TSFEL and tsfresh. For example, in TSFEL, 90% of the variance across 390 features can be captured with just four PCs. Finally, we introduce a metric for quantifying overlap between pairs of feature sets, which indicates substantial overlap. We found that the largest feature set, hctsa, is the most comprehensive, and that tsfresh is the most distinctive, due to its incorporation of many low-level Fourier coefficients. Our results provide empirical understanding of the differences between existing feature sets, information that can be used to better tailor feature sets to their applications.

Feature-based time-series analysis

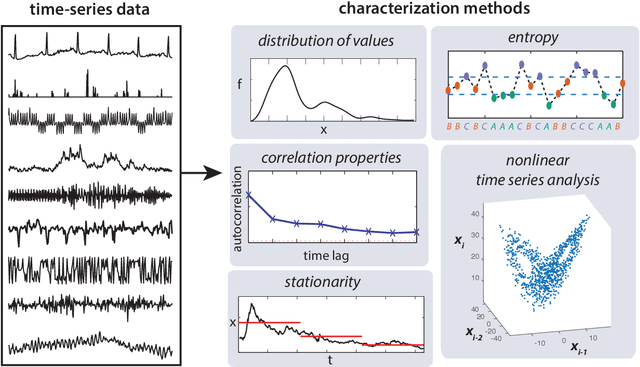
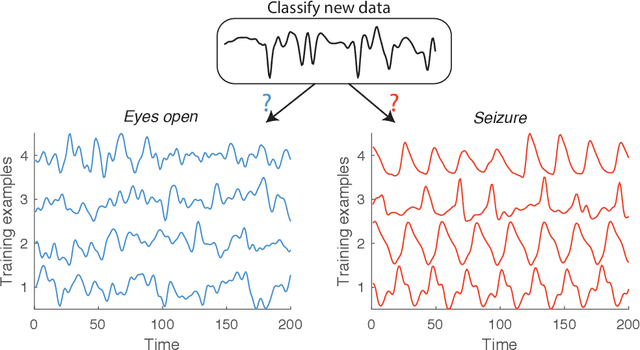
This work presents an introduction to feature-based time-series analysis. The time series as a data type is first described, along with an overview of the interdisciplinary time-series analysis literature. I then summarize the range of feature-based representations for time series that have been developed to aid interpretable insights into time-series structure. Particular emphasis is given to emerging research that facilitates wide comparison of feature-based representations that allow us to understand the properties of a time-series dataset that make it suited to a particular feature-based representation or analysis algorithm. The future of time-series analysis is likely to embrace approaches that exploit machine learning methods to partially automate human learning to aid understanding of the complex dynamical patterns in the time series we measure from the world.

Highly comparative feature-based time-series classification

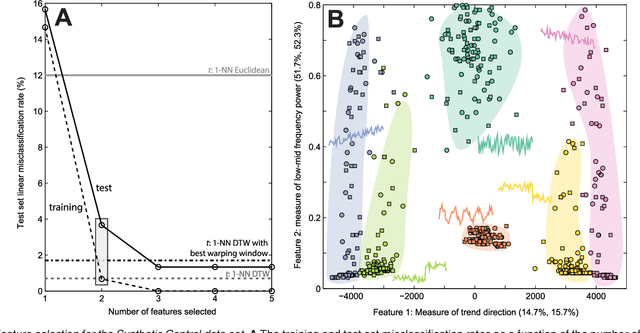
A highly comparative, feature-based approach to time series classification is introduced that uses an extensive database of algorithms to extract thousands of interpretable features from time series. These features are derived from across the scientific time-series analysis literature, and include summaries of time series in terms of their correlation structure, distribution, entropy, stationarity, scaling properties, and fits to a range of time-series models. After computing thousands of features for each time series in a training set, those that are most informative of the class structure are selected using greedy forward feature selection with a linear classifier. The resulting feature-based classifiers automatically learn the differences between classes using a reduced number of time-series properties, and circumvent the need to calculate distances between time series. Representing time series in this way results in orders of magnitude of dimensionality reduction, allowing the method to perform well on very large datasets containing long time series or time series of different lengths. For many of the datasets studied, classification performance exceeded that of conventional instance-based classifiers, including one nearest neighbor classifiers using Euclidean distances and dynamic time warping and, most importantly, the features selected provide an understanding of the properties of the dataset, insight that can guide further scientific investigation.

Highly comparative time-series analysis: The empirical structure of time series and their methods

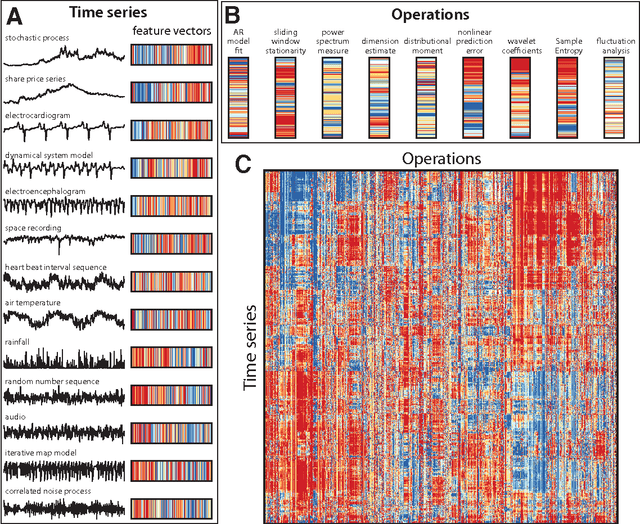
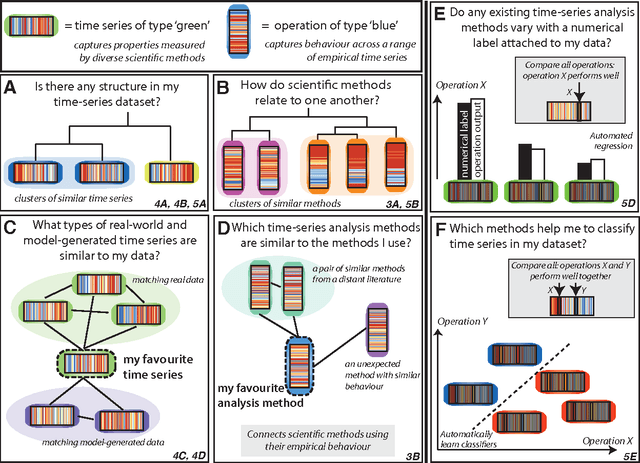
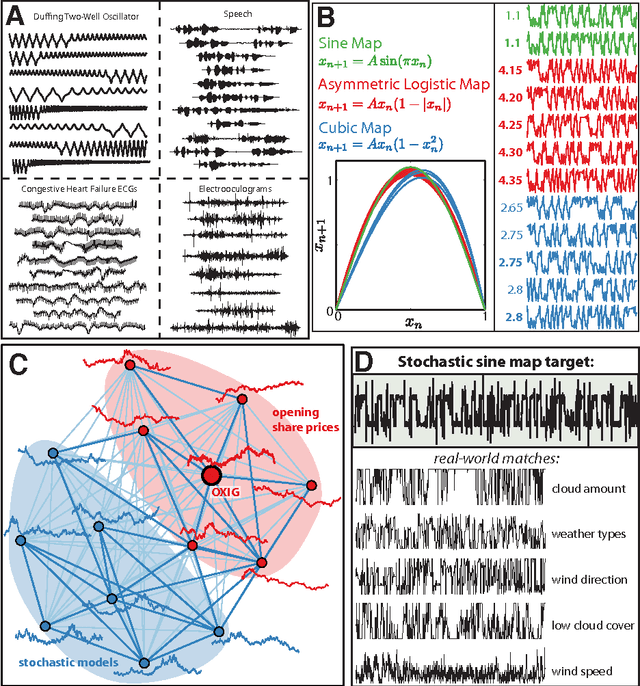
The process of collecting and organizing sets of observations represents a common theme throughout the history of science. However, despite the ubiquity of scientists measuring, recording, and analyzing the dynamics of different processes, an extensive organization of scientific time-series data and analysis methods has never been performed. Addressing this, annotated collections of over 35 000 real-world and model-generated time series and over 9000 time-series analysis algorithms are analyzed in this work. We introduce reduced representations of both time series, in terms of their properties measured by diverse scientific methods, and of time-series analysis methods, in terms of their behaviour on empirical time series, and use them to organize these interdisciplinary resources. This new approach to comparing across diverse scientific data and methods allows us to organize time-series datasets automatically according to their properties, retrieve alternatives to particular analysis methods developed in other scientific disciplines, and automate the selection of useful methods for time-series classification and regression tasks. The broad scientific utility of these tools is demonstrated on datasets of electroencephalograms, self-affine time series, heart beat intervals, speech signals, and others, in each case contributing novel analysis techniques to the existing literature. Highly comparative techniques that compare across an interdisciplinary literature can thus be used to guide more focused research in time-series analysis for applications across the scientific disciplines.