Unifying Pairwise Interactions in Complex Dynamics

Scientists have developed hundreds of techniques to measure the interactions between pairs of processes in complex systems. But these computational methods -- from correlation coefficients to causal inference -- rely on distinct quantitative theories that remain largely disconnected. Here we introduce a library of 249 statistics for pairwise interactions and assess their behavior on 1053 multivariate time series from a wide range of real-world and model-generated systems. Our analysis highlights new commonalities between different mathematical formulations, providing a unified picture of a rich, interdisciplinary literature. We then show that leveraging many methods from across science can uncover those most suitable for addressing a given problem, yielding high accuracy and interpretable understanding. Our framework is provided in extendable open software, enabling comprehensive data-driven analysis by integrating decades of methodological advances.

An Information Criterion for Inferring Coupling in Distributed Dynamical Systems

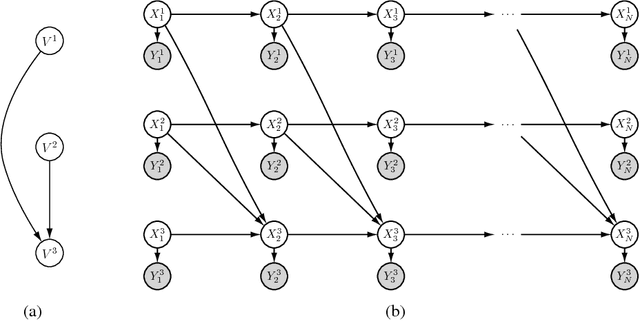
The behaviour of many real-world phenomena can be modelled by nonlinear dynamical systems whereby a latent system state is observed through a filter. We are interested in interacting subsystems of this form, which we model by a set of coupled maps as a synchronous update graph dynamical systems. Specifically, we study the structure learning problem for spatially distributed dynamical systems coupled via a directed acyclic graph. Unlike established structure learning procedures that find locally maximum posterior probabilities of a network structure containing latent variables, our work exploits the properties of dynamical systems to compute globally optimal approximations of these distributions. We arrive at this result by the use of time delay embedding theorems. Taking an information-theoretic perspective, we show that the log-likelihood has an intuitive interpretation in terms of information transfer.

Inferring Coupling of Distributed Dynamical Systems via Transfer Entropy

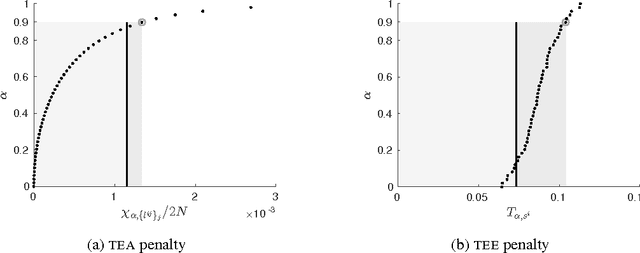
In this work, we are interested in structure learning for a set of spatially distributed dynamical systems, where individual subsystems are coupled via latent variables and observed through a filter. We represent this model as a directed acyclic graph (DAG) that characterises the unidirectional coupling between subsystems. Standard approaches to structure learning are not applicable in this framework due to the hidden variables, however we can exploit the properties of certain dynamical systems to formulate exact methods based on state space reconstruction. We approach the problem by using reconstruction theorems to analytically derive a tractable expression for the KL-divergence of a candidate DAG from the observed dataset. We show this measure can be decomposed as a function of two information-theoretic measures, transfer entropy and stochastic interaction. We then present two mathematically robust scoring functions based on transfer entropy and statistical independence tests. These results support the previously held conjecture that transfer entropy can be used to infer effective connectivity in complex networks.