BBK: a simpler, faster algorithm for enumerating maximal bicliques in large sparse bipartite graphs

Bipartite graphs are a prevalent modeling tool for real-world networks, capturing interactions between vertices of two different types. Within this framework, bicliques emerge as crucial structures when studying dense subgraphs: they are sets of vertices such that all vertices of the first type interact with all vertices of the second type. Therefore, they allow identifying groups of closely related vertices of the network, such as individuals with similar interests or webpages with similar contents. This article introduces a new algorithm designed for the exhaustive enumeration of maximal bicliques within a bipartite graph. This algorithm, called BBK for Bipartite Bron-Kerbosch, is a new extension to the bipartite case of the Bron-Kerbosch algorithm, which enumerates the maximal cliques in standard (non-bipartite) graphs. It is faster than the state-of-the-art algorithms and allows the enumeration on massive bipartite graphs that are not manageable with existing implementations. We analyze it theoretically to establish two complexity formulas: one as a function of the input and one as a function of the output characteristics of the algorithm. We also provide an open-access implementation of BBK in C++, which we use to experiment and validate its efficiency on massive real-world datasets and show that its execution time is shorter in practice than state-of-the art algorithms. These experiments also show that the order in which the vertices are processed, as well as the choice of one of the two types of vertices on which to initiate the enumeration have an impact on the computation time.

LSCPM: communities in massive real-world Link Streams by Clique Percolation Method

Community detection is a popular approach to understand the organization of interactions in static networks. For that purpose, the Clique Percolation Method (CPM), which involves the percolation of k-cliques, is a well-studied technique that offers several advantages. Besides, studying interactions that occur over time is useful in various contexts, which can be modeled by the link stream formalism. The Dynamic Clique Percolation Method (DCPM) has been proposed for extending CPM to temporal networks. However, existing implementations are unable to handle massive datasets. We present a novel algorithm that adapts CPM to link streams, which has the advantage that it allows us to speed up the computation time with respect to the existing DCPM method. We evaluate it experimentally on real datasets and show that it scales to massive link streams. For example, it allows to obtain a complete set of communities in under twenty-five minutes for a dataset with thirty million links, what the state of the art fails to achieve even after a week of computation. We further show that our method provides communities similar to DCPM, but slightly more aggregated. We exhibit the relevance of the obtained communities in real world cases, and show that they provide information on the importance of vertices in the link streams.

Faster maximal clique enumeration in large real-world link streams

Link streams offer a good model for representing interactions over time. They consist of links $(b,e,u,v)$, where $u$ and $v$ are vertices interacting during the whole time interval $[b,e]$. In this paper, we deal with the problem of enumerating maximal cliques in link streams. A clique is a pair $(C,[t_0,t_1])$, where $C$ is a set of vertices that all interact pairwise during the full interval $[t_0,t_1]$. It is maximal when neither its set of vertices nor its time interval can be increased. Some of the main works solving this problem are based on the famous Bron-Kerbosch algorithm for enumerating maximal cliques in graphs. We take this idea as a starting point to propose a new algorithm which matches the cliques of the instantaneous graphs formed by links existing at a given time $t$ to the maximal cliques of the link stream. We prove its validity and compute its complexity, which is better than the state-of-the art ones in many cases of interest. We also study the output-sensitive complexity, which is close to the output size, thereby showing that our algorithm is efficient. To confirm this, we perform experiments on link streams used in the state of the art, and on massive link streams, up to 100 million links. In all cases our algorithm is faster, mostly by a factor of at least 10 and up to a factor of $10^4$. Moreover, it scales to massive link streams for which the existing algorithms are not able to provide the solution.

Measuring Diversity in Heterogeneous Information Networks

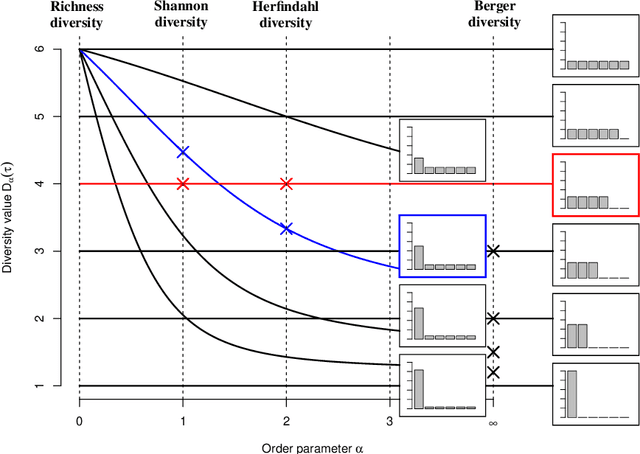
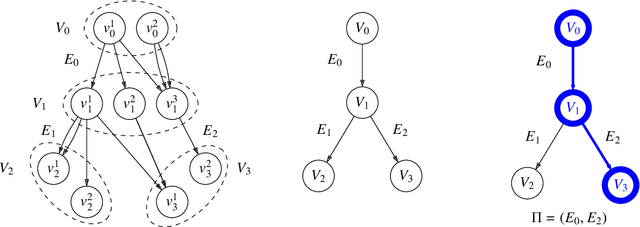
Diversity is a concept relevant to numerous domains of research varying from ecology, to information theory, and to economics, to cite a few. It is a notion that is steadily gaining attention in the information retrieval, network analysis, and artificial neural networks communities. While the use of diversity measures in network-structured data counts a growing number of applications, no clear and comprehensive description is available for the different ways in which diversities can be measured. In this article, we develop a formal framework for the application of a large family of diversity measures to heterogeneous information networks (HINs), a flexible, widely-used network data formalism. This extends the application of diversity measures, from systems of classifications and apportionments, to more complex relations that can be better modeled by networks. In doing so, we not only provide an effective organization of multiple practices from different domains, but also unearth new observables in systems modeled by heterogeneous information networks. We illustrate the pertinence of our approach by developing different applications related to various domains concerned by both diversity and networks. In particular, we illustrate the usefulness of these new proposed observables in the domains of recommender systems and social media studies, among other fields.

RankMerging: A supervised learning-to-rank framework to predict links in large social network

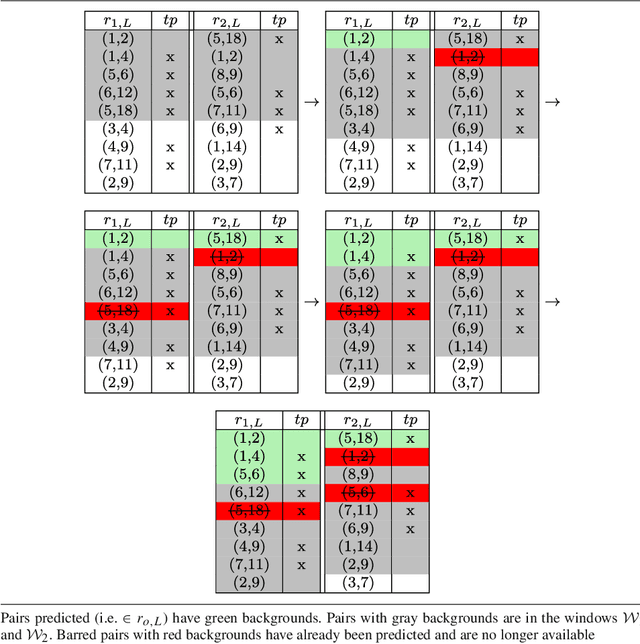
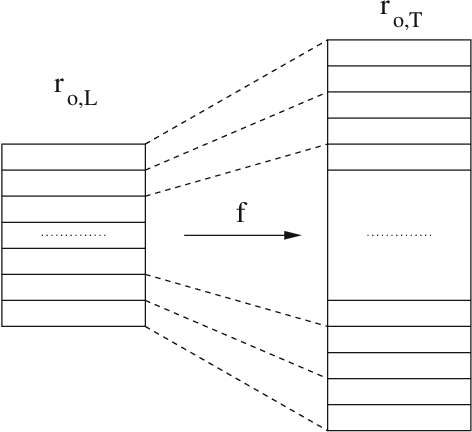
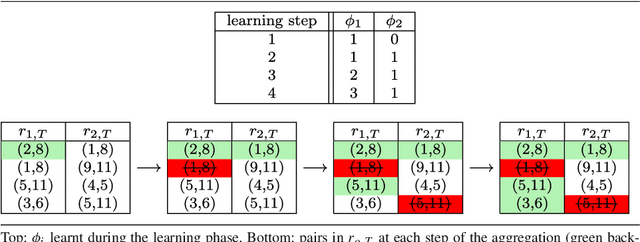
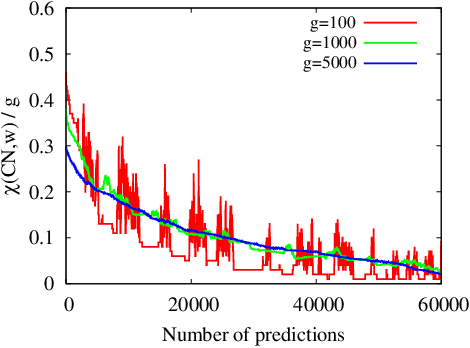
Uncovering unknown or missing links in social networks is a difficult task because of their sparsity and because links may represent different types of relationships, characterized by different structural patterns. In this paper, we define a simple yet efficient supervised learning-to-rank framework, called RankMerging, which aims at combining information provided by various unsupervised rankings. We illustrate our method on three different kinds of social networks and show that it substantially improves the performances of unsupervised metrics of ranking. We also compare it to other combination strategies based on standard methods. Finally, we explore various aspects of RankMerging, such as feature selection and parameter estimation and discuss its area of relevance: the prediction of an adjustable number of links on large networks.