Measuring Diversity in Heterogeneous Information Networks

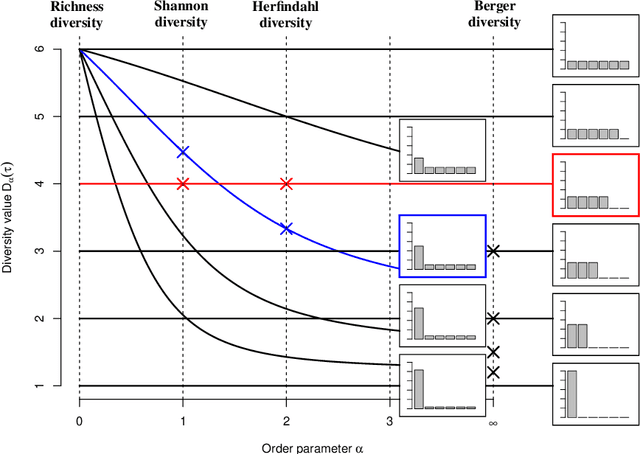
Diversity is a concept relevant to numerous domains of research varying from ecology, to information theory, and to economics, to cite a few. It is a notion that is steadily gaining attention in the information retrieval, network analysis, and artificial neural networks communities. While the use of diversity measures in network-structured data counts a growing number of applications, no clear and comprehensive description is available for the different ways in which diversities can be measured. In this article, we develop a formal framework for the application of a large family of diversity measures to heterogeneous information networks (HINs), a flexible, widely-used network data formalism. This extends the application of diversity measures, from systems of classifications and apportionments, to more complex relations that can be better modeled by networks. In doing so, we not only provide an effective organization of multiple practices from different domains, but also unearth new observables in systems modeled by heterogeneous information networks. We illustrate the pertinence of our approach by developing different applications related to various domains concerned by both diversity and networks. In particular, we illustrate the usefulness of these new proposed observables in the domains of recommender systems and social media studies, among other fields.

An Information-theoretic Framework for the Lossy Compression of Link Streams

Graph compression is a data analysis technique that consists in the replacement of parts of a graph by more general structural patterns in order to reduce its description length. It notably provides interesting exploration tools for the study of real, large-scale, and complex graphs which cannot be grasped at first glance. This article proposes a framework for the compression of temporal graphs, that is for the compression of graphs that evolve with time. This framework first builds on a simple and limited scheme, exploiting structural equivalence for the lossless compression of static graphs, then generalises it to the lossy compression of link streams, a recent formalism for the study of temporal graphs. Such generalisation relies on the natural extension of (bidimensional) relational data by the addition of a third temporal dimension. Moreover, we introduce an information-theoretic measure to quantify and to control the information that is lost during compression, as well as an algebraic characterisation of the space of possible compression patterns to enhance the expressiveness of the initial compression scheme. These contributions lead to the definition of a combinatorial optimisation problem, that is the Lossy Multistream Compression Problem, for which we provide an exact algorithm.