Future Research Avenues for Artificial Intelligence in Digital Gaming: An Exploratory Report

Video games are a natural and synergistic application domain for artificial intelligence (AI) systems, offering both the potential to enhance player experience and immersion, as well as providing valuable benchmarks and virtual environments to advance AI technologies in general. This report presents a high-level overview of five promising research pathways for applying state-of-the-art AI methods, particularly deep learning, to digital gaming within the context of the current research landscape. The objective of this work is to outline a curated, non-exhaustive list of encouraging research directions at the intersection of AI and video games that may serve to inspire more rigorous and comprehensive research efforts in the future. We discuss (i) investigating large language models as core engines for game agent modelling, (ii) using neural cellular automata for procedural game content generation, (iii) accelerating computationally expensive in-game simulations via deep surrogate modelling, (iv) leveraging self-supervised learning to obtain useful video game state embeddings, and (v) training generative models of interactive worlds using unlabelled video data. We also briefly address current technical challenges associated with the integration of advanced deep learning systems into video game development, and indicate key areas where further progress is likely to be beneficial.

Investigating Graph Neural Networks and Classical Feature-Extraction Techniques in Activity-Cliff and Molecular Property Prediction

Molecular featurisation refers to the transformation of molecular data into numerical feature vectors. It is one of the key research areas in molecular machine learning and computational drug discovery. Recently, message-passing graph neural networks (GNNs) have emerged as a novel method to learn differentiable features directly from molecular graphs. While such techniques hold great promise, further investigations are needed to clarify if and when they indeed manage to definitively outcompete classical molecular featurisations such as extended-connectivity fingerprints (ECFPs) and physicochemical-descriptor vectors (PDVs). We systematically explore and further develop classical and graph-based molecular featurisation methods for two important tasks: molecular property prediction, in particular, quantitative structure-activity relationship (QSAR) prediction, and the largely unexplored challenge of activity-cliff (AC) prediction. We first give a technical description and critical analysis of PDVs, ECFPs and message-passing GNNs, with a focus on graph isomorphism networks (GINs). We then conduct a rigorous computational study to compare the performance of PDVs, ECFPs and GINs for QSAR and AC-prediction. Following this, we mathematically describe and computationally evaluate a novel twin neural network model for AC-prediction. We further introduce an operation called substructure pooling for the vectorisation of structural fingerprints as a natural counterpart to graph pooling in GNN architectures. We go on to propose Sort & Slice, a simple substructure-pooling technique for ECFPs that robustly outperforms hash-based folding at molecular property prediction. Finally, we outline two ideas for future research: (i) a graph-based self-supervised learning strategy to make classical molecular featurisations trainable, and (ii) trainable substructure-pooling via differentiable self-attention.

Exploring QSAR Models for Activity-Cliff Prediction

Pairs of similar compounds that only differ by a small structural modification but exhibit a large difference in their binding affinity for a given target are known as activity cliffs (ACs). It has been hypothesised that quantitative structure-activity relationship (QSAR) models struggle to predict ACs and that ACs thus form a major source of prediction error. However, a study to explore the AC-prediction power of modern QSAR methods and its relationship to general QSAR-prediction performance is lacking. We systematically construct nine distinct QSAR models by combining three molecular representation methods (extended-connectivity fingerprints, physicochemical-descriptor vectors and graph isomorphism networks) with three regression techniques (random forests, k-nearest neighbours and multilayer perceptrons); we then use each resulting model to classify pairs of similar compounds as ACs or non-ACs and to predict the activities of individual molecules in three case studies: dopamine receptor D2, factor Xa, and SARS-CoV-2 main protease. We observe low AC-sensitivity amongst the tested models when the activities of both compounds are unknown, but a substantial increase in AC-sensitivity when the actual activity of one of the compounds is given. Graph isomorphism features are found to be competitive with or superior to classical molecular representations for AC-classification and can thus be employed as baseline AC-prediction models or simple compound-optimisation tools. For general QSAR-prediction, however, extended-connectivity fingerprints still consistently deliver the best performance. Our results provide strong support for the hypothesis that indeed QSAR methods frequently fail to predict ACs. We propose twin-network training for deep learning models as a potential future pathway to increase AC-sensitivity and thus overall QSAR performance.

Numerically Solving Parametric Families of High-Dimensional Kolmogorov Partial Differential Equations via Deep Learning

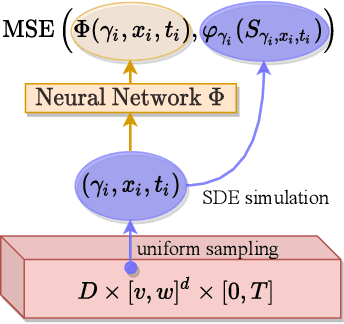
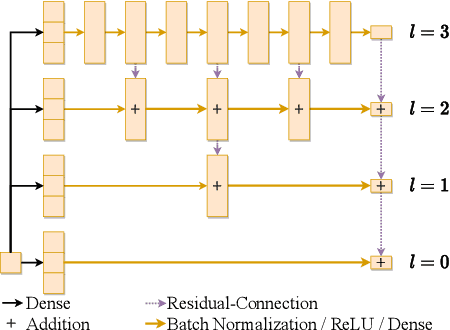
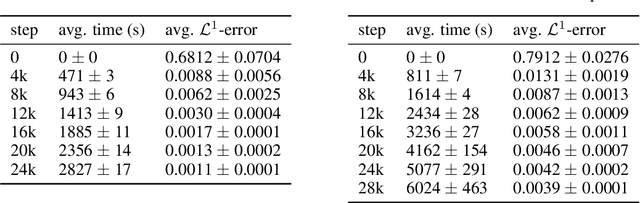
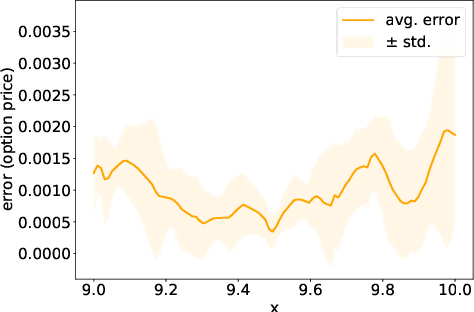
We present a deep learning algorithm for the numerical solution of parametric families of high-dimensional linear Kolmogorov partial differential equations (PDEs). Our method is based on reformulating the numerical approximation of a whole family of Kolmogorov PDEs as a single statistical learning problem using the Feynman-Kac formula. Successful numerical experiments are presented, which empirically confirm the functionality and efficiency of our proposed algorithm in the case of heat equations and Black-Scholes option pricing models parametrized by affine-linear coefficient functions. We show that a single deep neural network trained on simulated data is capable of learning the solution functions of an entire family of PDEs on a full space-time region. Most notably, our numerical observations and theoretical results also demonstrate that the proposed method does not suffer from the curse of dimensionality, distinguishing it from almost all standard numerical methods for PDEs.