Adapting to Non-stationarity with Growing Expert Ensembles
Paper and Code
Jun 28, 2011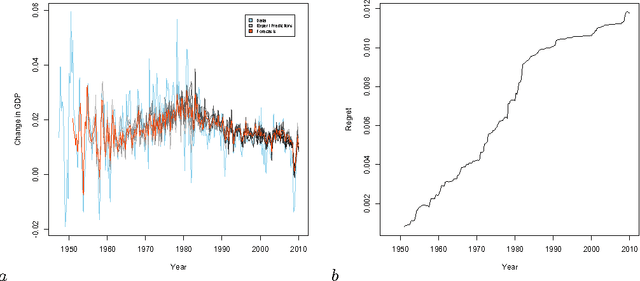
When dealing with time series with complex non-stationarities, low retrospective regret on individual realizations is a more appropriate goal than low prospective risk in expectation. Online learning algorithms provide powerful guarantees of this form, and have often been proposed for use with non-stationary processes because of their ability to switch between different forecasters or ``experts''. However, existing methods assume that the set of experts whose forecasts are to be combined are all given at the start, which is not plausible when dealing with a genuinely historical or evolutionary system. We show how to modify the ``fixed shares'' algorithm for tracking the best expert to cope with a steadily growing set of experts, obtained by fitting new models to new data as it becomes available, and obtain regret bounds for the growing ensemble.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge