Blind Construction of Optimal Nonlinear Recursive Predictors for Discrete Sequences

We present a new method for nonlinear prediction of discrete random sequences under minimal structural assumptions. We give a mathematical construction for optimal predictors of such processes, in the form of hidden Markov models. We then describe an algorithm, CSSR (Causal-State Splitting Reconstruction), which approximates the ideal predictor from data. We discuss the reliability of CSSR, its data requirements, and its performance in simulations. Finally, we compare our approach to existing methods using variablelength Markov models and cross-validated hidden Markov models, and show theoretically and experimentally that our method delivers results superior to the former and at least comparable to the latter.

Adapting to Non-stationarity with Growing Expert Ensembles

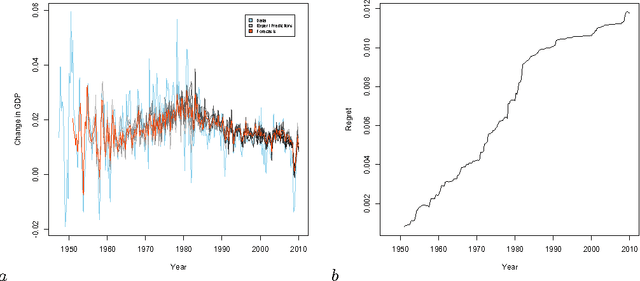
When dealing with time series with complex non-stationarities, low retrospective regret on individual realizations is a more appropriate goal than low prospective risk in expectation. Online learning algorithms provide powerful guarantees of this form, and have often been proposed for use with non-stationary processes because of their ability to switch between different forecasters or ``experts''. However, existing methods assume that the set of experts whose forecasts are to be combined are all given at the start, which is not plausible when dealing with a genuinely historical or evolutionary system. We show how to modify the ``fixed shares'' algorithm for tracking the best expert to cope with a steadily growing set of experts, obtained by fitting new models to new data as it becomes available, and obtain regret bounds for the growing ensemble.

The Computational Structure of Spike Trains

Neurons perform computations, and convey the results of those computations through the statistical structure of their output spike trains. Here we present a practical method, grounded in the information-theoretic analysis of prediction, for inferring a minimal representation of that structure and for characterizing its complexity. Starting from spike trains, our approach finds their causal state models (CSMs), the minimal hidden Markov models or stochastic automata capable of generating statistically identical time series. We then use these CSMs to objectively quantify both the generalizable structure and the idiosyncratic randomness of the spike train. Specifically, we show that the expected algorithmic information content (the information needed to describe the spike train exactly) can be split into three parts describing (1) the time-invariant structure (complexity) of the minimal spike-generating process, which describes the spike train statistically; (2) the randomness (internal entropy rate) of the minimal spike-generating process; and (3) a residual pure noise term not described by the minimal spike-generating process. We use CSMs to approximate each of these quantities. The CSMs are inferred nonparametrically from the data, making only mild regularity assumptions, via the causal state splitting reconstruction algorithm. The methods presented here complement more traditional spike train analyses by describing not only spiking probability and spike train entropy, but also the complexity of a spike train's structure. We demonstrate our approach using both simulated spike trains and experimental data recorded in rat barrel cortex during vibrissa stimulation.