Undecidability of Underfitting in Learning Algorithms

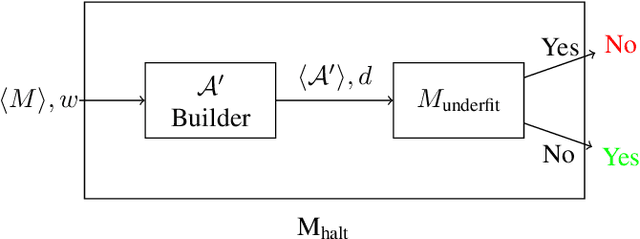
Using recent machine learning results that present an information-theoretic perspective on underfitting and overfitting, we prove that deciding whether an encodable learning algorithm will always underfit a dataset, even if given unlimited training time, is undecidable. We discuss the importance of this result and potential topics for further research, including information-theoretic and probabilistic strategies for bounding learning algorithm fit.

An Information-Theoretic Perspective on Overfitting and Underfitting

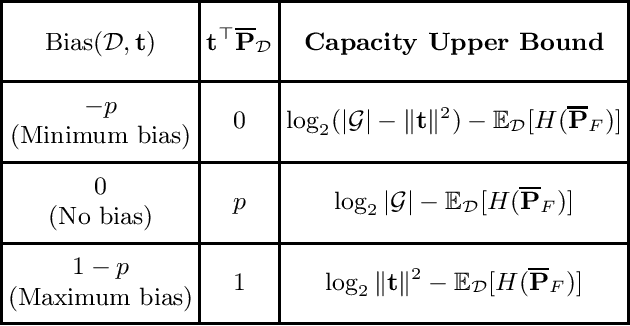
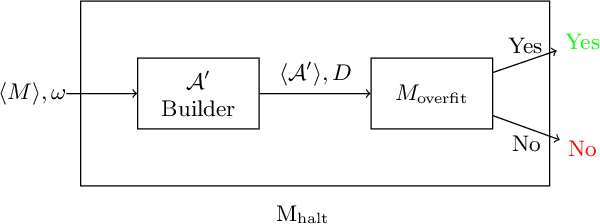
We present an information-theoretic framework for understanding overfitting and underfitting in machine learning and prove the formal undecidability of determining whether an arbitrary classification algorithm will overfit a dataset. Measuring algorithm capacity via the information transferred from datasets to models, we consider mismatches between algorithm capacities and datasets to provide a signature for when a model can overfit or underfit a dataset. We present results upper-bounding algorithm capacity, establish its relationship to quantities in the algorithmic search framework for machine learning, and relate our work to recent information-theoretic approaches to generalization.

Limits of Transfer Learning

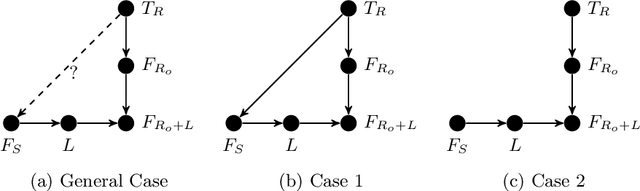
Transfer learning involves taking information and insight from one problem domain and applying it to a new problem domain. Although widely used in practice, theory for transfer learning remains less well-developed. To address this, we prove several novel results related to transfer learning, showing the need to carefully select which sets of information to transfer and the need for dependence between transferred information and target problems. Furthermore, we prove how the degree of probabilistic change in an algorithm using transfer learning places an upper bound on the amount of improvement possible. These results build on the algorithmic search framework for machine learning, allowing the results to apply to a wide range of learning problems using transfer.

The Bias-Expressivity Trade-off

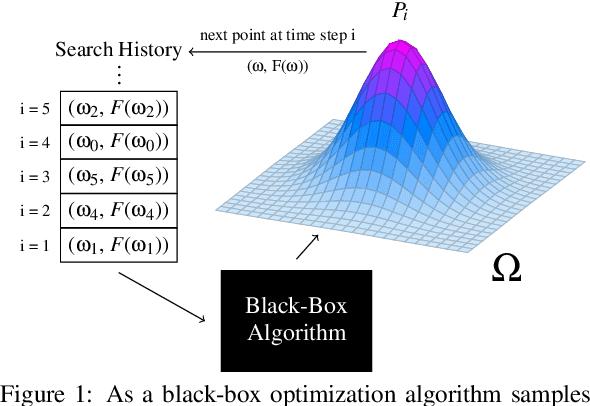
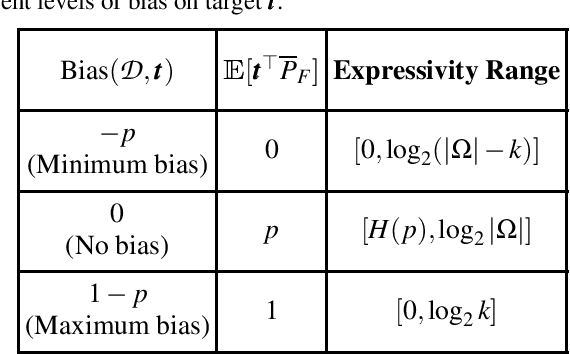
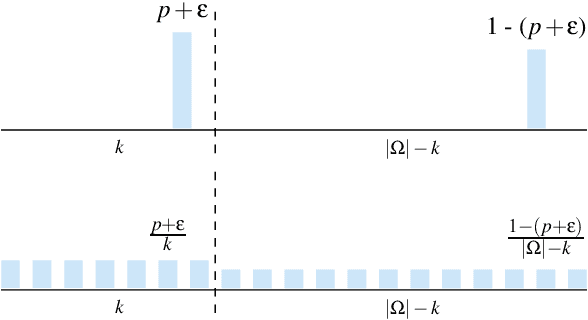
Learning algorithms need bias to generalize and perform better than random guessing. We examine the flexibility (expressivity) of biased algorithms. An expressive algorithm can adapt to changing training data, altering its outcome based on changes in its input. We measure expressivity by using an information-theoretic notion of entropy on algorithm outcome distributions, demonstrating a trade-off between bias and expressivity. To the degree an algorithm is biased is the degree to which it can outperform uniform random sampling, but is also the degree to which is becomes inflexible. We derive bounds relating bias to expressivity, proving the necessary trade-offs inherent in trying to create strongly performing yet flexible algorithms.

The Futility of Bias-Free Learning and Search

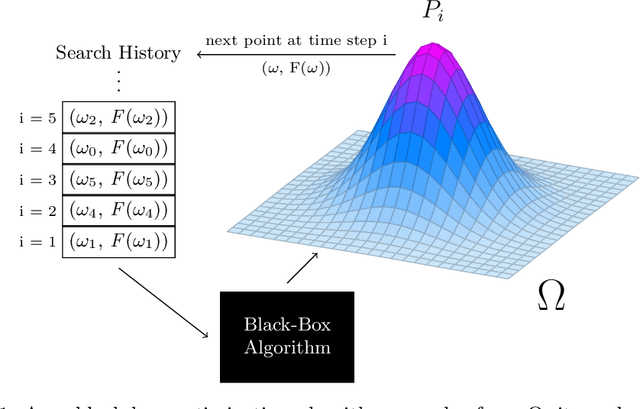
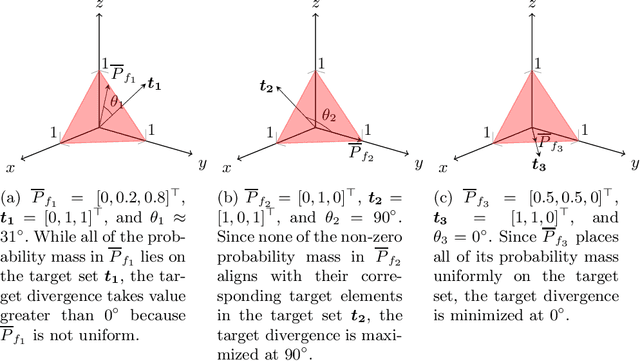
Building on the view of machine learning as search, we demonstrate the necessity of bias in learning, quantifying the role of bias (measured relative to a collection of possible datasets, or more generally, information resources) in increasing the probability of success. For a given degree of bias towards a fixed target, we show that the proportion of favorable information resources is strictly bounded from above. Furthermore, we demonstrate that bias is a conserved quantity, such that no algorithm can be favorably biased towards many distinct targets simultaneously. Thus bias encodes trade-offs. The probability of success for a task can also be measured geometrically, as the angle of agreement between what holds for the actual task and what is assumed by the algorithm, represented in its bias. Lastly, finding a favorably biasing distribution over a fixed set of information resources is provably difficult, unless the set of resources itself is already favorable with respect to the given task and algorithm.

The Famine of Forte: Few Search Problems Greatly Favor Your Algorithm

Casting machine learning as a type of search, we demonstrate that the proportion of problems that are favorable for a fixed algorithm is strictly bounded, such that no single algorithm can perform well over a large fraction of them. Our results explain why we must either continue to develop new learning methods year after year or move towards highly parameterized models that are both flexible and sensitive to their hyperparameters. We further give an upper bound on the expected performance for a search algorithm as a function of the mutual information between the target and the information resource (e.g., training dataset), proving the importance of certain types of dependence for machine learning. Lastly, we show that the expected per-query probability of success for an algorithm is mathematically equivalent to a single-query probability of success under a distribution (called a search strategy), and prove that the proportion of favorable strategies is also strictly bounded. Thus, whether one holds fixed the search algorithm and considers all possible problems or one fixes the search problem and looks at all possible search strategies, favorable matches are exceedingly rare. The forte (strength) of any algorithm is quantifiably restricted.

The LICORS Cabinet: Nonparametric Algorithms for Spatio-temporal Prediction

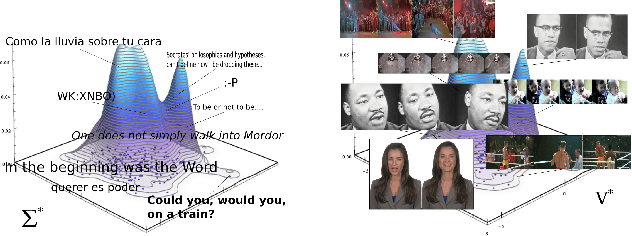
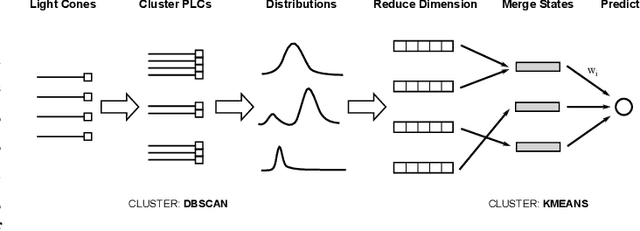
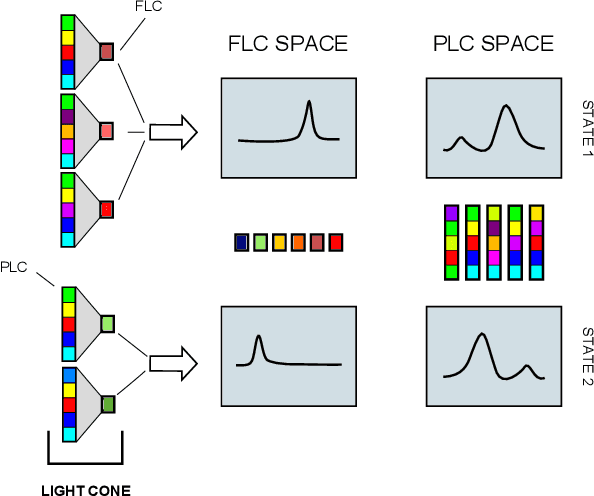
Spatio-temporal data is intrinsically high dimensional, so unsupervised modeling is only feasible if we can exploit structure in the process. When the dynamics are local in both space and time, this structure can be exploited by splitting the global field into many lower-dimensional "light cones". We review light cone decompositions for predictive state reconstruction, introducing three simple light cone algorithms. These methods allow for tractable inference of spatio-temporal data, such as full-frame video. The algorithms make few assumptions on the underlying process yet have good predictive performance and can provide distributions over spatio-temporal data, enabling sophisticated probabilistic inference.