Huey Sun
Limits of Transfer Learning
Jun 23, 2020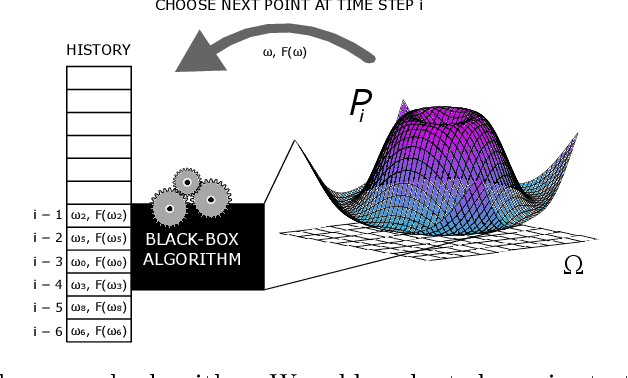
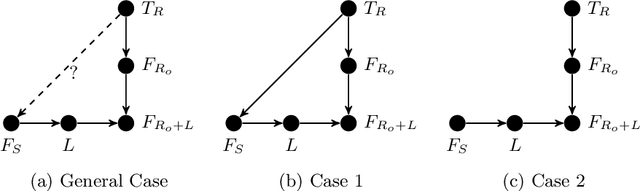
Abstract:Transfer learning involves taking information and insight from one problem domain and applying it to a new problem domain. Although widely used in practice, theory for transfer learning remains less well-developed. To address this, we prove several novel results related to transfer learning, showing the need to carefully select which sets of information to transfer and the need for dependence between transferred information and target problems. Furthermore, we prove how the degree of probabilistic change in an algorithm using transfer learning places an upper bound on the amount of improvement possible. These results build on the algorithmic search framework for machine learning, allowing the results to apply to a wide range of learning problems using transfer.
Decomposable Probability-of-Success Metrics in Algorithmic Search
Jan 03, 2020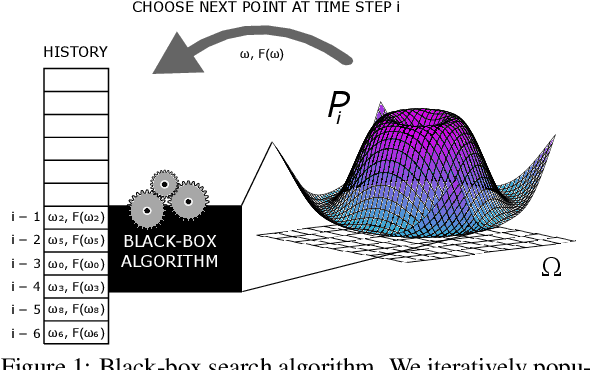
Abstract:Previous studies have used a specific success metric within an algorithmic search framework to prove machine learning impossibility results. However, this specific success metric prevents us from applying these results on other forms of machine learning, e.g. transfer learning. We define decomposable metrics as a category of success metrics for search problems which can be expressed as a linear operation on a probability distribution to solve this issue. Using an arbitrary decomposable metric to measure the success of a search, we demonstrate theorems which bound success in various ways, generalizing several existing results in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge