Tyler Sam
The Limits of Transfer Reinforcement Learning with Latent Low-rank Structure
Oct 28, 2024Abstract:Many reinforcement learning (RL) algorithms are too costly to use in practice due to the large sizes $S, A$ of the problem's state and action space. To resolve this issue, we study transfer RL with latent low rank structure. We consider the problem of transferring a latent low rank representation when the source and target MDPs have transition kernels with Tucker rank $(S , d, A )$, $(S , S , d), (d, S, A )$, or $(d , d , d )$. In each setting, we introduce the transfer-ability coefficient $\alpha$ that measures the difficulty of representational transfer. Our algorithm learns latent representations in each source MDP and then exploits the linear structure to remove the dependence on $S, A $, or $S A$ in the target MDP regret bound. We complement our positive results with information theoretic lower bounds that show our algorithms (excluding the ($d, d, d$) setting) are minimax-optimal with respect to $\alpha$.
Overcoming the Long Horizon Barrier for Sample-Efficient Reinforcement Learning with Latent Low-Rank Structure
Jun 07, 2022
Abstract:The practicality of reinforcement learning algorithms has been limited due to poor scaling with respect to the problem size, as the sample complexity of learning an $\epsilon$-optimal policy is $\Tilde{\Omega}\left(|S||A|H^3 / \eps^2\right)$ over worst case instances of an MDP with state space $S$, action space $A$, and horizon $H$. We consider a class of MDPs that exhibit low rank structure, where the latent features are unknown. We argue that a natural combination of value iteration and low-rank matrix estimation results in an estimation error that grows doubly exponentially in the horizon $H$. We then provide a new algorithm along with statistical guarantees that efficiently exploits low rank structure given access to a generative model, achieving a sample complexity of $\Tilde{O}\left(d^5(|S|+|A|)\mathrm{poly}(H)/\eps^2\right)$ for a rank $d$ setting, which is minimax optimal with respect to the scaling of $|S|, |A|$, and $\eps$. In contrast to literature on linear and low-rank MDPs, we do not require a known feature mapping, our algorithm is computationally simple, and our results hold for long time horizons. Our results provide insights on the minimal low-rank structural assumptions required on the MDP with respect to the transition kernel versus the optimal action-value function.
Limits of Transfer Learning
Jun 23, 2020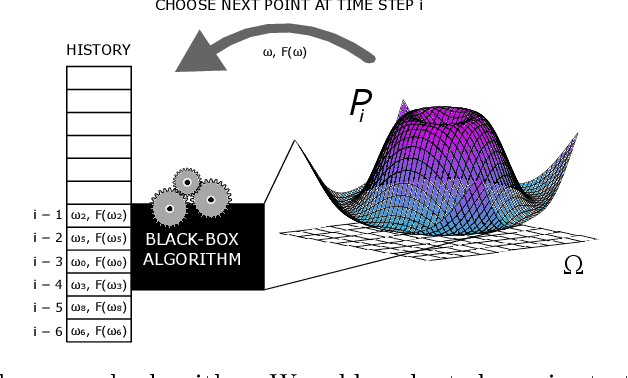
Abstract:Transfer learning involves taking information and insight from one problem domain and applying it to a new problem domain. Although widely used in practice, theory for transfer learning remains less well-developed. To address this, we prove several novel results related to transfer learning, showing the need to carefully select which sets of information to transfer and the need for dependence between transferred information and target problems. Furthermore, we prove how the degree of probabilistic change in an algorithm using transfer learning places an upper bound on the amount of improvement possible. These results build on the algorithmic search framework for machine learning, allowing the results to apply to a wide range of learning problems using transfer.
Decomposable Probability-of-Success Metrics in Algorithmic Search
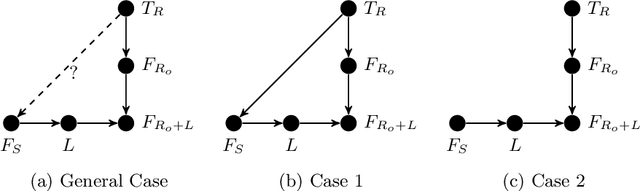
Jan 03, 2020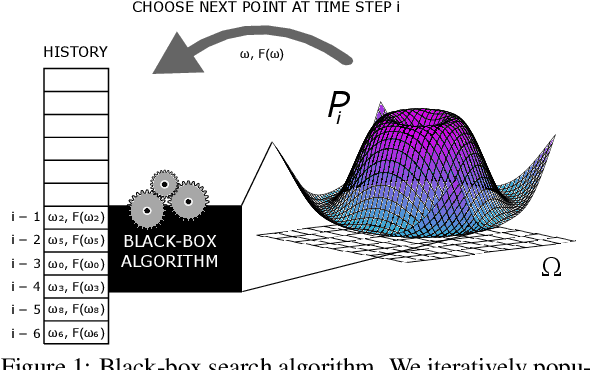
Abstract:Previous studies have used a specific success metric within an algorithmic search framework to prove machine learning impossibility results. However, this specific success metric prevents us from applying these results on other forms of machine learning, e.g. transfer learning. We define decomposable metrics as a category of success metrics for search problems which can be expressed as a linear operation on a probability distribution to solve this issue. Using an arbitrary decomposable metric to measure the success of a search, we demonstrate theorems which bound success in various ways, generalizing several existing results in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge