The Labeling Distribution Matrix : A Tool for Estimating Machine Learning Algorithm Capacity

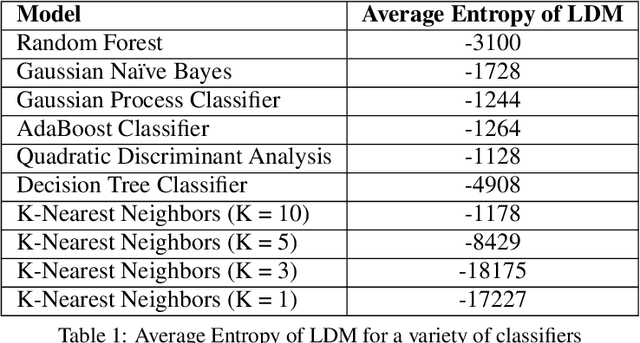
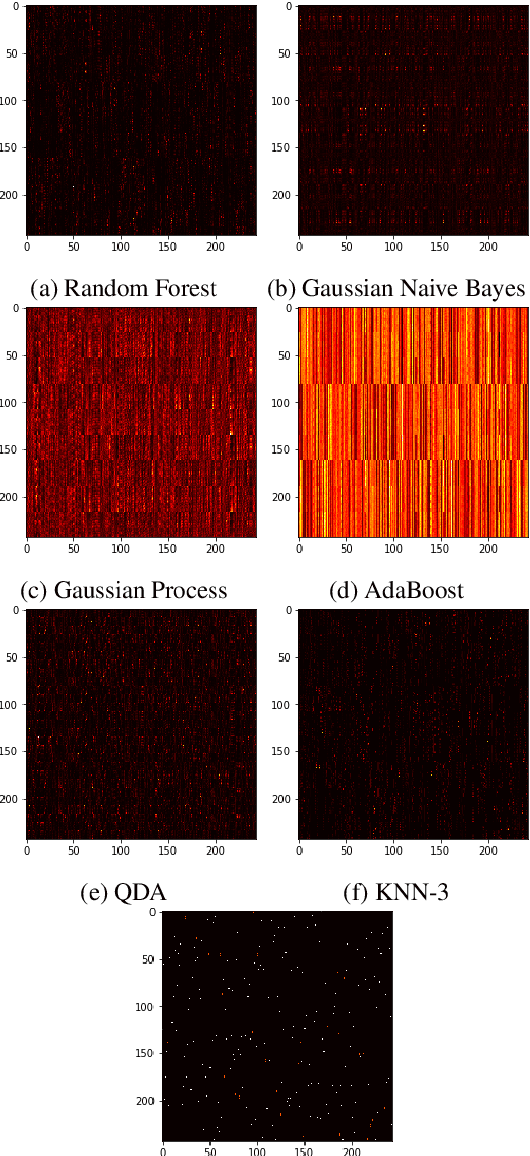
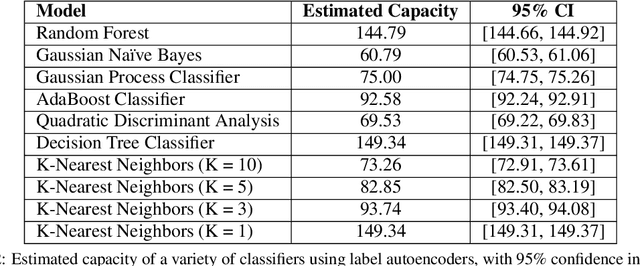
Algorithm performance in supervised learning is a combination of memorization, generalization, and luck. By estimating how much information an algorithm can memorize from a dataset, we can set a lower bound on the amount of performance due to other factors such as generalization and luck. With this goal in mind, we introduce the Labeling Distribution Matrix (LDM) as a tool for estimating the capacity of learning algorithms. The method attempts to characterize the diversity of possible outputs by an algorithm for different training datasets, using this to measure algorithm flexibility and responsiveness to data. We test the method on several supervised learning algorithms, and find that while the results are not conclusive, the LDM does allow us to gain potentially valuable insight into the prediction behavior of algorithms. We also introduce the Label Recorder as an additional tool for estimating algorithm capacity, with more promising initial results.

Decomposable Probability-of-Success Metrics in Algorithmic Search

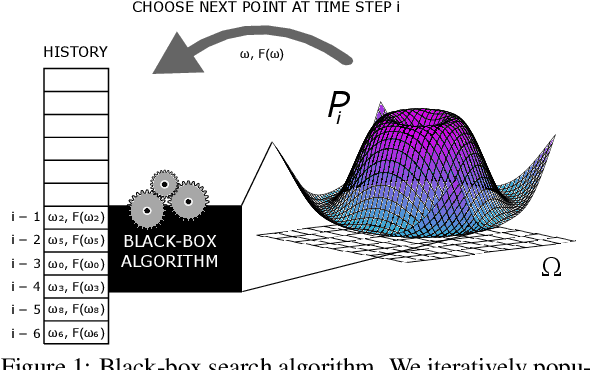
Previous studies have used a specific success metric within an algorithmic search framework to prove machine learning impossibility results. However, this specific success metric prevents us from applying these results on other forms of machine learning, e.g. transfer learning. We define decomposable metrics as a category of success metrics for search problems which can be expressed as a linear operation on a probability distribution to solve this issue. Using an arbitrary decomposable metric to measure the success of a search, we demonstrate theorems which bound success in various ways, generalizing several existing results in the literature.