The Labeling Distribution Matrix : A Tool for Estimating Machine Learning Algorithm Capacity

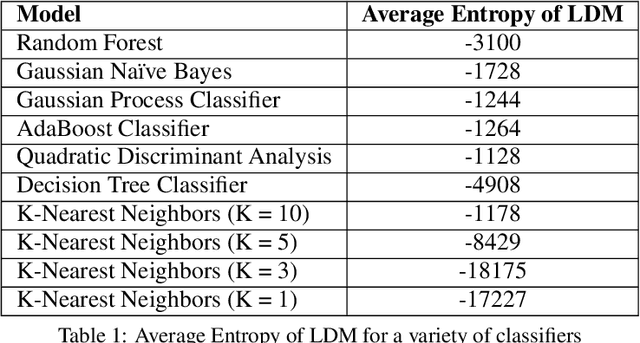
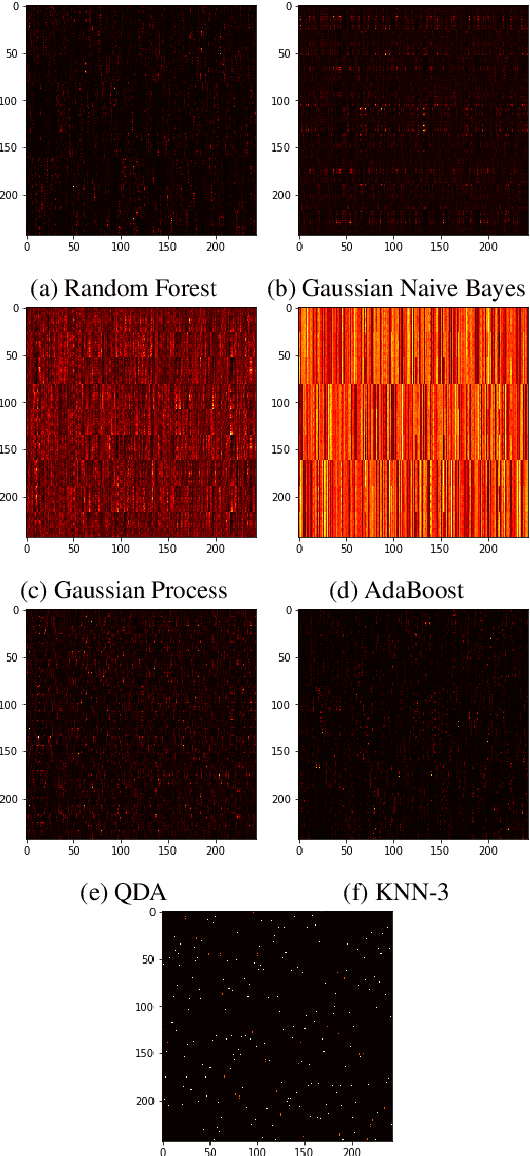
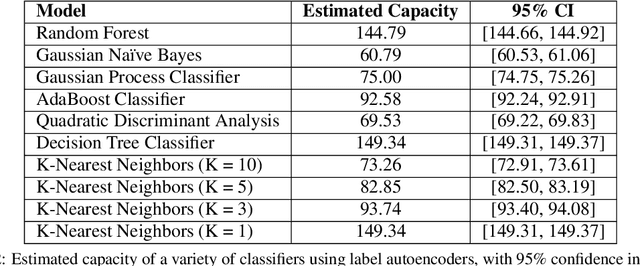
Algorithm performance in supervised learning is a combination of memorization, generalization, and luck. By estimating how much information an algorithm can memorize from a dataset, we can set a lower bound on the amount of performance due to other factors such as generalization and luck. With this goal in mind, we introduce the Labeling Distribution Matrix (LDM) as a tool for estimating the capacity of learning algorithms. The method attempts to characterize the diversity of possible outputs by an algorithm for different training datasets, using this to measure algorithm flexibility and responsiveness to data. We test the method on several supervised learning algorithms, and find that while the results are not conclusive, the LDM does allow us to gain potentially valuable insight into the prediction behavior of algorithms. We also introduce the Label Recorder as an additional tool for estimating algorithm capacity, with more promising initial results.

The Bias-Expressivity Trade-off

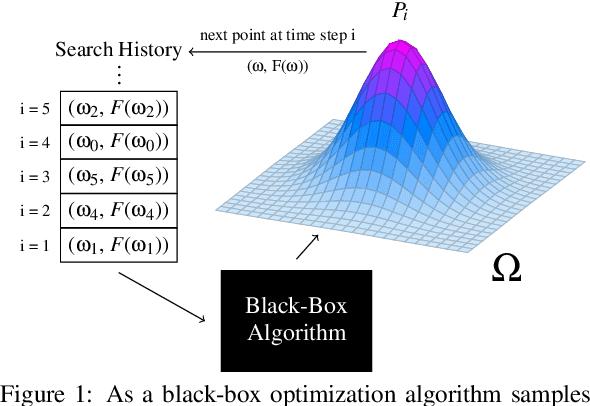
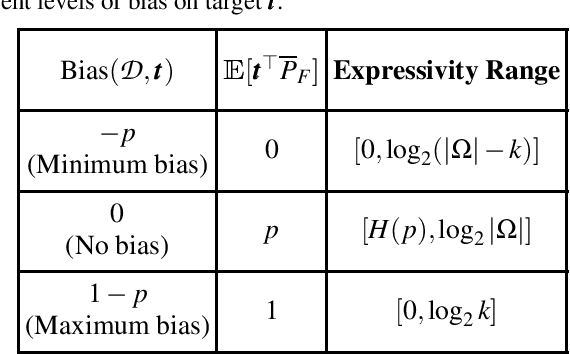
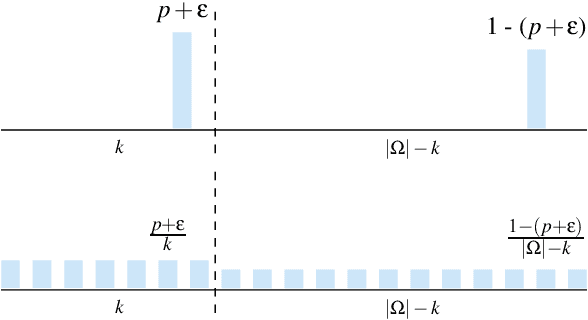
Learning algorithms need bias to generalize and perform better than random guessing. We examine the flexibility (expressivity) of biased algorithms. An expressive algorithm can adapt to changing training data, altering its outcome based on changes in its input. We measure expressivity by using an information-theoretic notion of entropy on algorithm outcome distributions, demonstrating a trade-off between bias and expressivity. To the degree an algorithm is biased is the degree to which it can outperform uniform random sampling, but is also the degree to which is becomes inflexible. We derive bounds relating bias to expressivity, proving the necessary trade-offs inherent in trying to create strongly performing yet flexible algorithms.

The Futility of Bias-Free Learning and Search

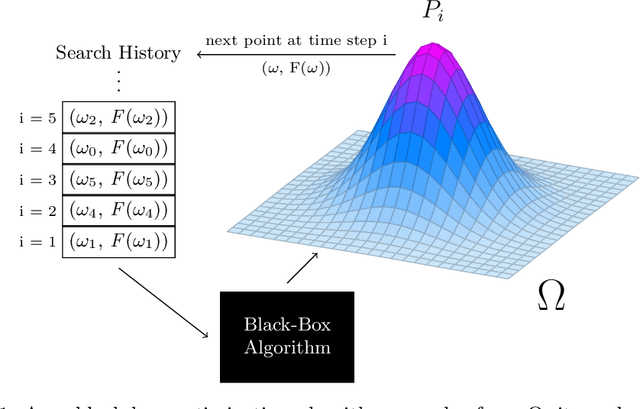
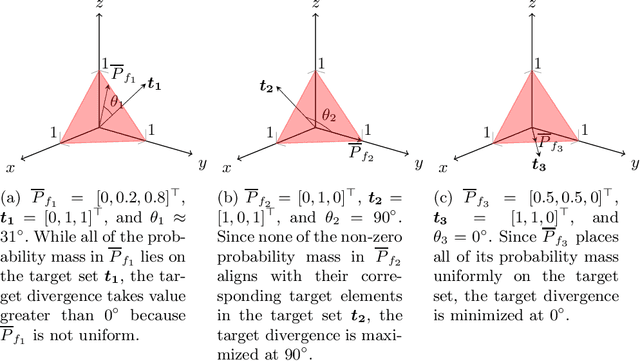
Building on the view of machine learning as search, we demonstrate the necessity of bias in learning, quantifying the role of bias (measured relative to a collection of possible datasets, or more generally, information resources) in increasing the probability of success. For a given degree of bias towards a fixed target, we show that the proportion of favorable information resources is strictly bounded from above. Furthermore, we demonstrate that bias is a conserved quantity, such that no algorithm can be favorably biased towards many distinct targets simultaneously. Thus bias encodes trade-offs. The probability of success for a task can also be measured geometrically, as the angle of agreement between what holds for the actual task and what is assumed by the algorithm, represented in its bias. Lastly, finding a favorably biasing distribution over a fixed set of information resources is provably difficult, unless the set of resources itself is already favorable with respect to the given task and algorithm.