Julia Vendemiatti
The Bias-Expressivity Trade-off
Nov 09, 2019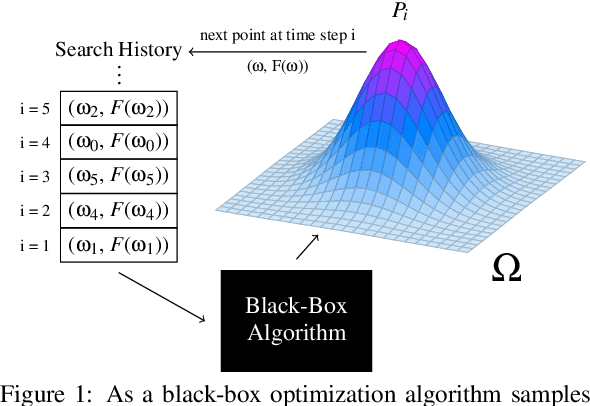
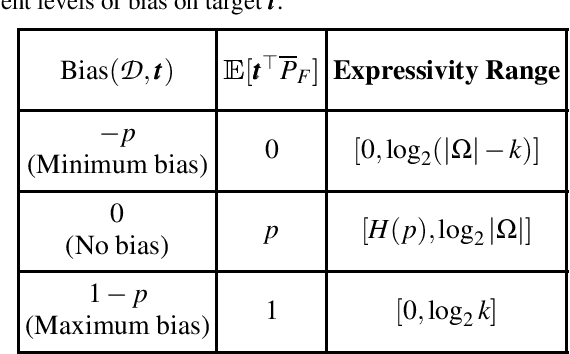

Abstract:Learning algorithms need bias to generalize and perform better than random guessing. We examine the flexibility (expressivity) of biased algorithms. An expressive algorithm can adapt to changing training data, altering its outcome based on changes in its input. We measure expressivity by using an information-theoretic notion of entropy on algorithm outcome distributions, demonstrating a trade-off between bias and expressivity. To the degree an algorithm is biased is the degree to which it can outperform uniform random sampling, but is also the degree to which is becomes inflexible. We derive bounds relating bias to expressivity, proving the necessary trade-offs inherent in trying to create strongly performing yet flexible algorithms.
The Futility of Bias-Free Learning and Search
Jul 13, 2019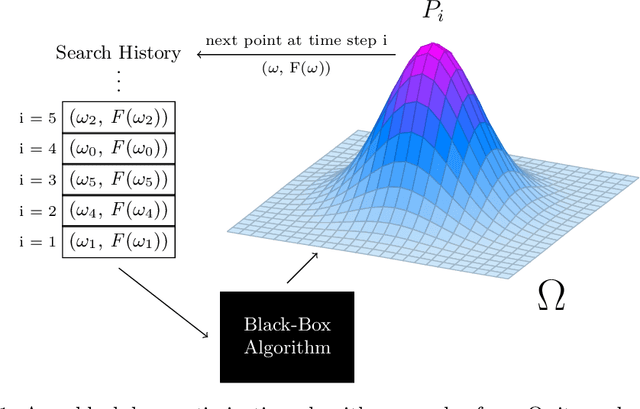
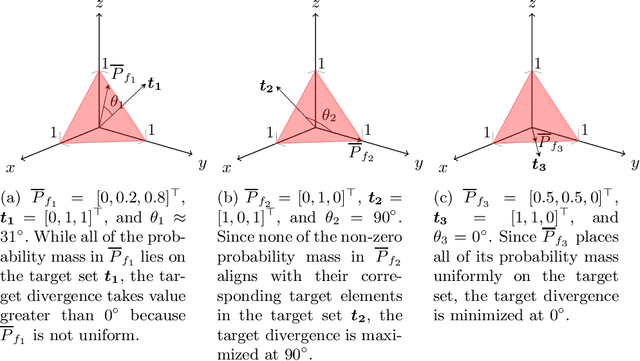
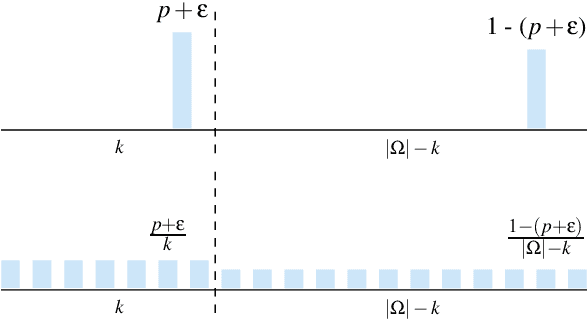
Abstract:Building on the view of machine learning as search, we demonstrate the necessity of bias in learning, quantifying the role of bias (measured relative to a collection of possible datasets, or more generally, information resources) in increasing the probability of success. For a given degree of bias towards a fixed target, we show that the proportion of favorable information resources is strictly bounded from above. Furthermore, we demonstrate that bias is a conserved quantity, such that no algorithm can be favorably biased towards many distinct targets simultaneously. Thus bias encodes trade-offs. The probability of success for a task can also be measured geometrically, as the angle of agreement between what holds for the actual task and what is assumed by the algorithm, represented in its bias. Lastly, finding a favorably biasing distribution over a fixed set of information resources is provably difficult, unless the set of resources itself is already favorable with respect to the given task and algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge