Hierarchical Action Recognition: A Contrastive Video-Language Approach with Hierarchical Interactions

Video recognition remains an open challenge, requiring the identification of diverse content categories within videos. Mainstream approaches often perform flat classification, overlooking the intrinsic hierarchical structure relating categories. To address this, we formalize the novel task of hierarchical video recognition, and propose a video-language learning framework tailored for hierarchical recognition. Specifically, our framework encodes dependencies between hierarchical category levels, and applies a top-down constraint to filter recognition predictions. We further construct a new fine-grained dataset based on medical assessments for rehabilitation of stroke patients, serving as a challenging benchmark for hierarchical recognition. Through extensive experiments, we demonstrate the efficacy of our approach for hierarchical recognition, significantly outperforming conventional methods, especially for fine-grained subcategories. The proposed framework paves the way for hierarchical modeling in video understanding tasks, moving beyond flat categorization.

Vertical Federated Learning Hybrid Local Pre-training

Vertical Federated Learning (VFL), which has a broad range of real-world applications, has received much attention in both academia and industry. Enterprises aspire to exploit more valuable features of the same users from diverse departments to boost their model prediction skills. VFL addresses this demand and concurrently secures individual parties from exposing their raw data. However, conventional VFL encounters a bottleneck as it only leverages aligned samples, whose size shrinks with more parties involved, resulting in data scarcity and the waste of unaligned data. To address this problem, we propose a novel VFL Hybrid Local Pre-training (VFLHLP) approach. VFLHLP first pre-trains local networks on the local data of participating parties. Then it utilizes these pre-trained networks to adjust the sub-model for the labeled party or enhance representation learning for other parties during downstream federated learning on aligned data, boosting the performance of federated models. The experimental results on real-world advertising datasets, demonstrate that our approach achieves the best performance over baseline methods by large margins. The ablation study further illustrates the contribution of each technique in VFLHLP to its overall performance.

Bayesian Model Selection of Stochastic Block Models

A central problem in analyzing networks is partitioning them into modules or communities. One of the best tools for this is the stochastic block model, which clusters vertices into blocks with statistically homogeneous pattern of links. Despite its flexibility and popularity, there has been a lack of principled statistical model selection criteria for the stochastic block model. Here we propose a Bayesian framework for choosing the number of blocks as well as comparing it to the more elaborate degree- corrected block models, ultimately leading to a universal model selection framework capable of comparing multiple modeling combinations. We will also investigate its connection to the minimum description length principle.

Model Selection for Degree-corrected Block Models

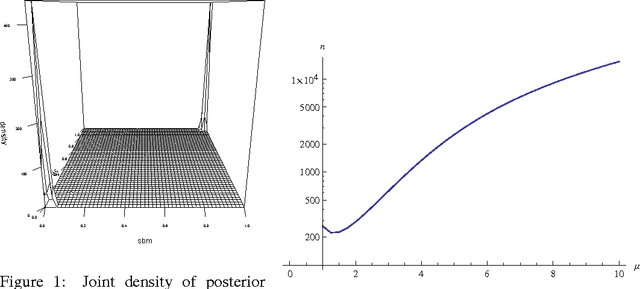
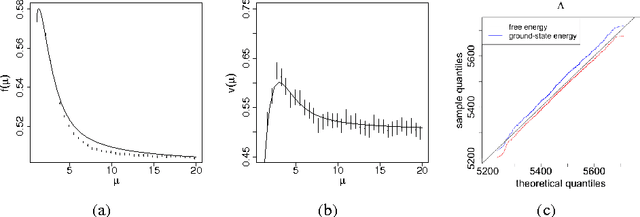
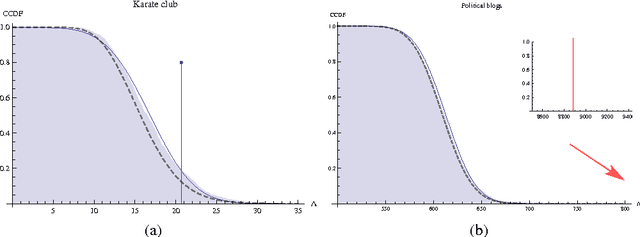
The proliferation of models for networks raises challenging problems of model selection: the data are sparse and globally dependent, and models are typically high-dimensional and have large numbers of latent variables. Together, these issues mean that the usual model-selection criteria do not work properly for networks. We illustrate these challenges, and show one way to resolve them, by considering the key network-analysis problem of dividing a graph into communities or blocks of nodes with homogeneous patterns of links to the rest of the network. The standard tool for doing this is the stochastic block model, under which the probability of a link between two nodes is a function solely of the blocks to which they belong. This imposes a homogeneous degree distribution within each block; this can be unrealistic, so degree-corrected block models add a parameter for each node, modulating its over-all degree. The choice between ordinary and degree-corrected block models matters because they make very different inferences about communities. We present the first principled and tractable approach to model selection between standard and degree-corrected block models, based on new large-graph asymptotics for the distribution of log-likelihood ratios under the stochastic block model, finding substantial departures from classical results for sparse graphs. We also develop linear-time approximations for log-likelihoods under both the stochastic block model and the degree-corrected model, using belief propagation. Applications to simulated and real networks show excellent agreement with our approximations. Our results thus both solve the practical problem of deciding on degree correction, and point to a general approach to model selection in network analysis.

Scalable Text and Link Analysis with Mixed-Topic Link Models

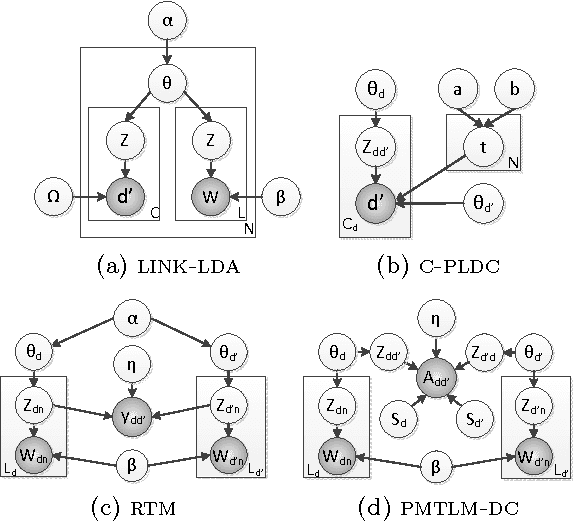
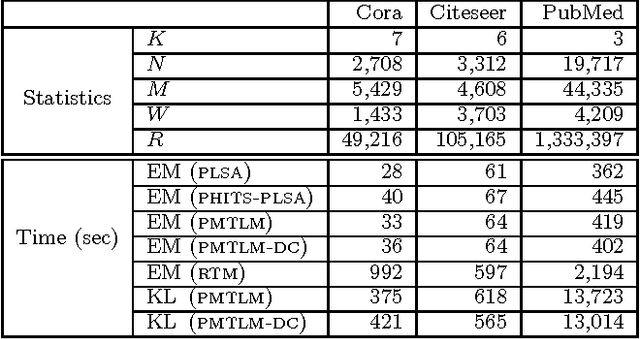
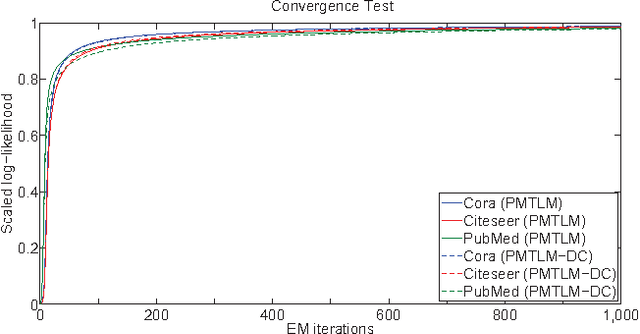
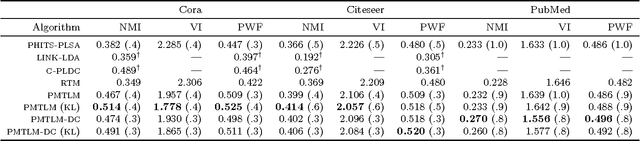
Many data sets contain rich information about objects, as well as pairwise relations between them. For instance, in networks of websites, scientific papers, and other documents, each node has content consisting of a collection of words, as well as hyperlinks or citations to other nodes. In order to perform inference on such data sets, and make predictions and recommendations, it is useful to have models that are able to capture the processes which generate the text at each node and the links between them. In this paper, we combine classic ideas in topic modeling with a variant of the mixed-membership block model recently developed in the statistical physics community. The resulting model has the advantage that its parameters, including the mixture of topics of each document and the resulting overlapping communities, can be inferred with a simple and scalable expectation-maximization algorithm. We test our model on three data sets, performing unsupervised topic classification and link prediction. For both tasks, our model outperforms several existing state-of-the-art methods, achieving higher accuracy with significantly less computation, analyzing a data set with 1.3 million words and 44 thousand links in a few minutes.

Oriented and Degree-generated Block Models: Generating and Inferring Communities with Inhomogeneous Degree Distributions

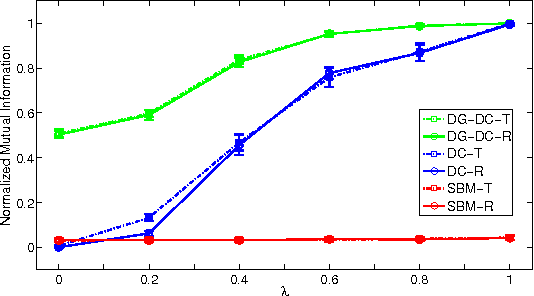
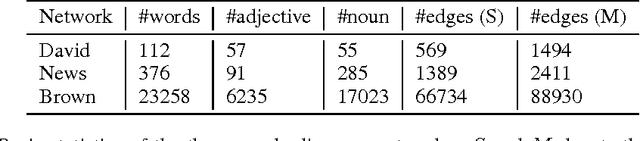
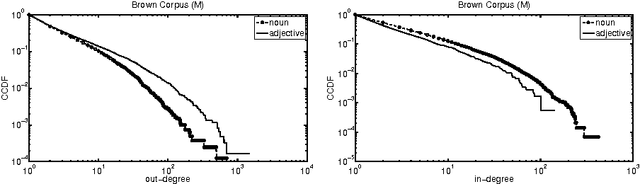
The stochastic block model is a powerful tool for inferring community structure from network topology. However, it predicts a Poisson degree distribution within each community, while most real-world networks have a heavy-tailed degree distribution. The degree-corrected block model can accommodate arbitrary degree distributions within communities. But since it takes the vertex degrees as parameters rather than generating them, it cannot use them to help it classify the vertices, and its natural generalization to directed graphs cannot even use the orientations of the edges. In this paper, we present variants of the block model with the best of both worlds: they can use vertex degrees and edge orientations in the classification process, while tolerating heavy-tailed degree distributions within communities. We show that for some networks, including synthetic networks and networks of word adjacencies in English text, these new block models achieve a higher accuracy than either standard or degree-corrected block models.

Active Learning for Node Classification in Assortative and Disassortative Networks

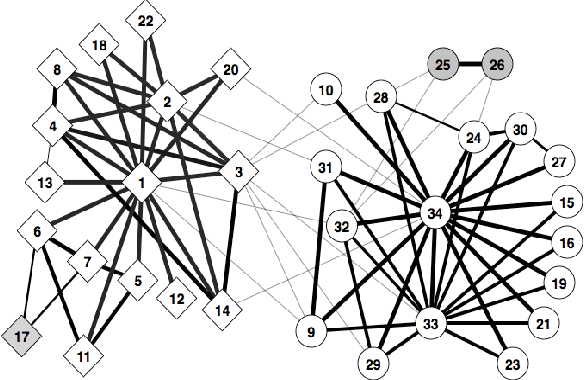
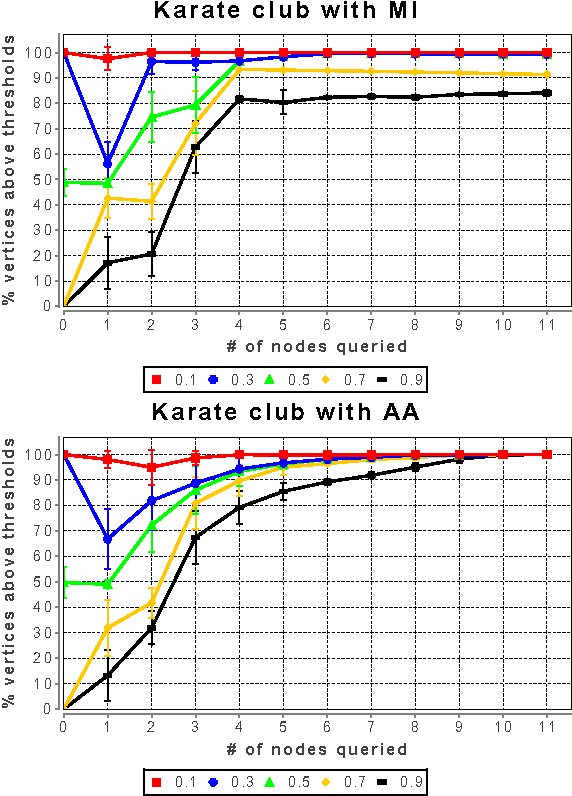
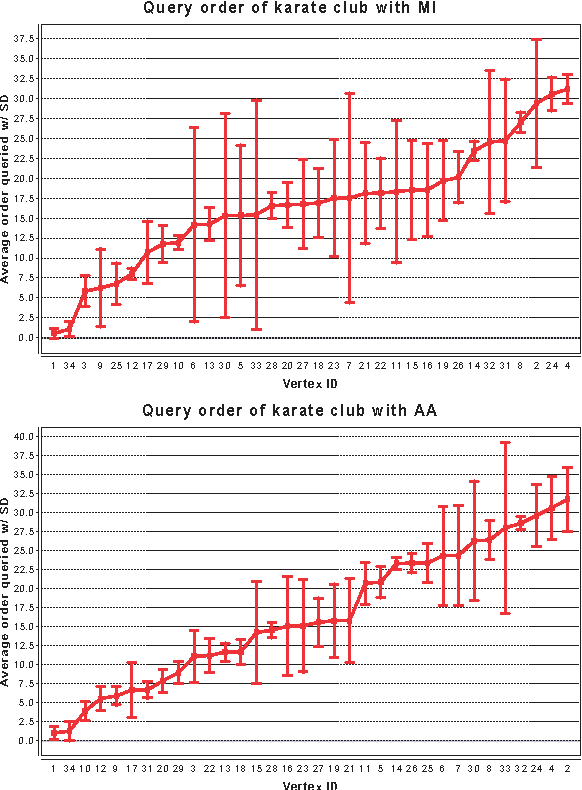
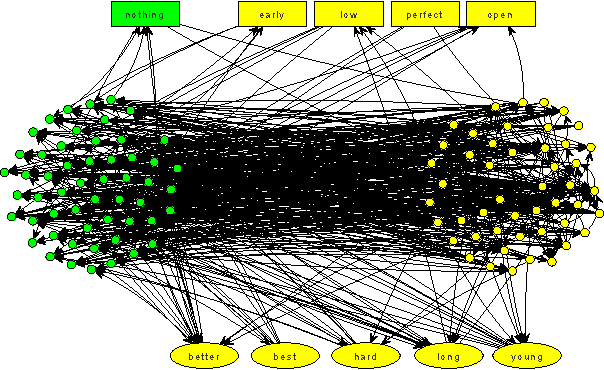
In many real-world networks, nodes have class labels, attributes, or variables that affect the network's topology. If the topology of the network is known but the labels of the nodes are hidden, we would like to select a small subset of nodes such that, if we knew their labels, we could accurately predict the labels of all the other nodes. We develop an active learning algorithm for this problem which uses information-theoretic techniques to choose which nodes to explore. We test our algorithm on networks from three different domains: a social network, a network of English words that appear adjacently in a novel, and a marine food web. Our algorithm makes no initial assumptions about how the groups connect, and performs well even when faced with quite general types of network structure. In particular, we do not assume that nodes of the same class are more likely to be connected to each other---only that they connect to the rest of the network in similar ways.

Active Learning for Hidden Attributes in Networks

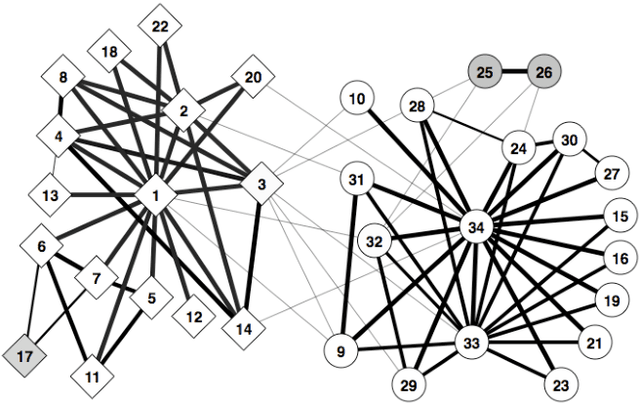
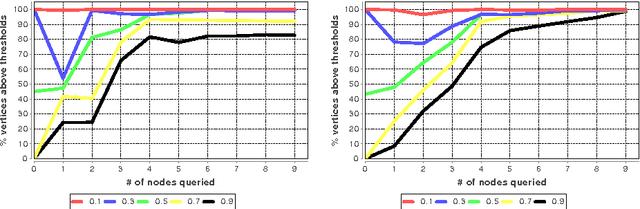
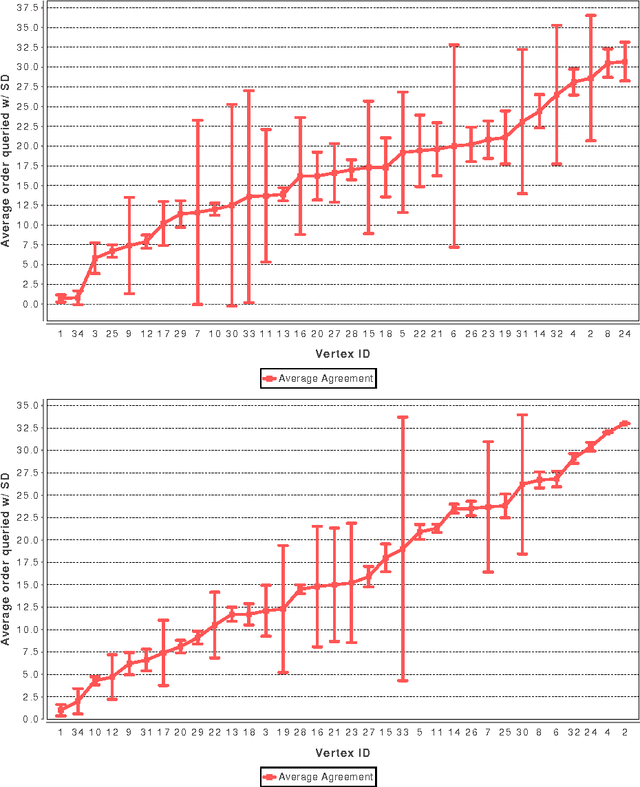
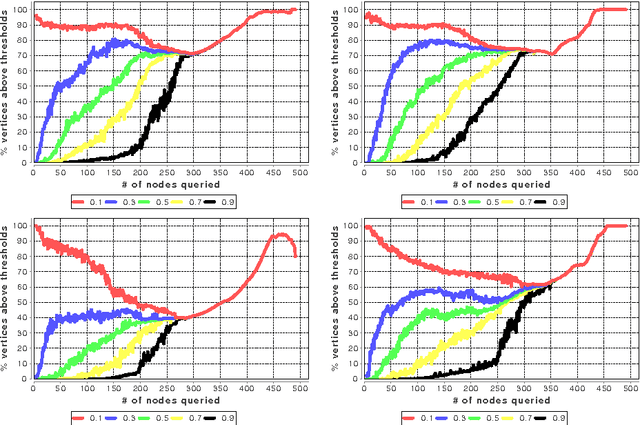
In many networks, vertices have hidden attributes, or types, that are correlated with the networks topology. If the topology is known but these attributes are not, and if learning the attributes is costly, we need a method for choosing which vertex to query in order to learn as much as possible about the attributes of the other vertices. We assume the network is generated by a stochastic block model, but we make no assumptions about its assortativity or disassortativity. We choose which vertex to query using two methods: 1) maximizing the mutual information between its attributes and those of the others (a well-known approach in active learning) and 2) maximizing the average agreement between two independent samples of the conditional Gibbs distribution. Experimental results show that both these methods do much better than simple heuristics. They also consistently identify certain vertices as important by querying them early on.