Bayesian Discovery of Multiple Bayesian Networks via Transfer Learning

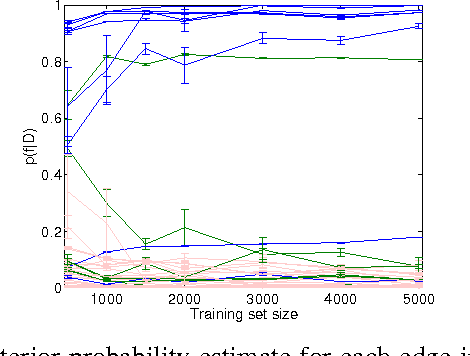
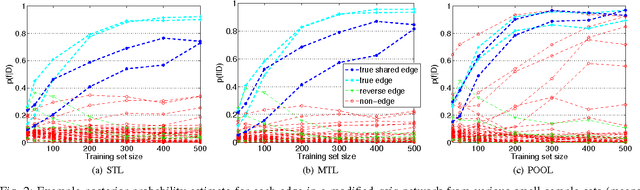
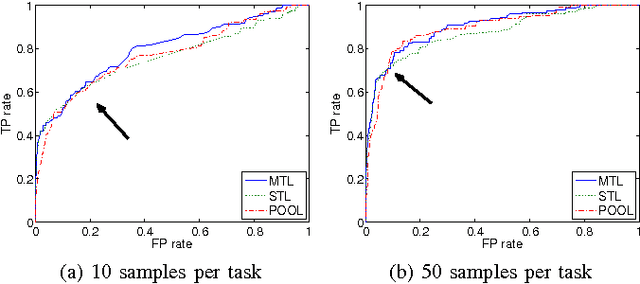
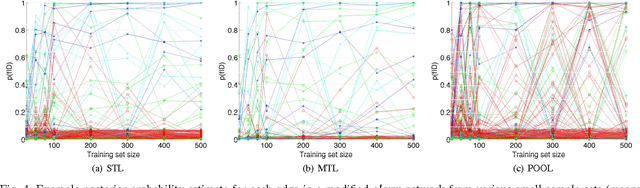
Bayesian network structure learning algorithms with limited data are being used in domains such as systems biology and neuroscience to gain insight into the underlying processes that produce observed data. Learning reliable networks from limited data is difficult, therefore transfer learning can improve the robustness of learned networks by leveraging data from related tasks. Existing transfer learning algorithms for Bayesian network structure learning give a single maximum a posteriori estimate of network models. Yet, many other models may be equally likely, and so a more informative result is provided by Bayesian structure discovery. Bayesian structure discovery algorithms estimate posterior probabilities of structural features, such as edges. We present transfer learning for Bayesian structure discovery which allows us to explore the shared and unique structural features among related tasks. Efficient computation requires that our transfer learning objective factors into local calculations, which we prove is given by a broad class of transfer biases. Theoretically, we show the efficiency of our approach. Empirically, we show that compared to single task learning, transfer learning is better able to positively identify true edges. We apply the method to whole-brain neuroimaging data.

Smoothness and Structure Learning by Proxy

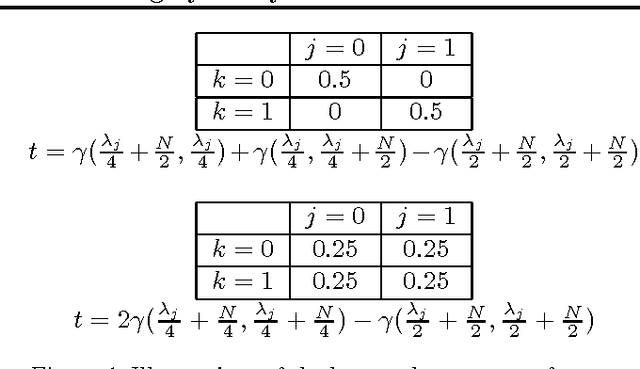
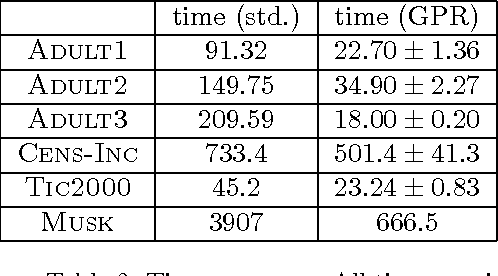
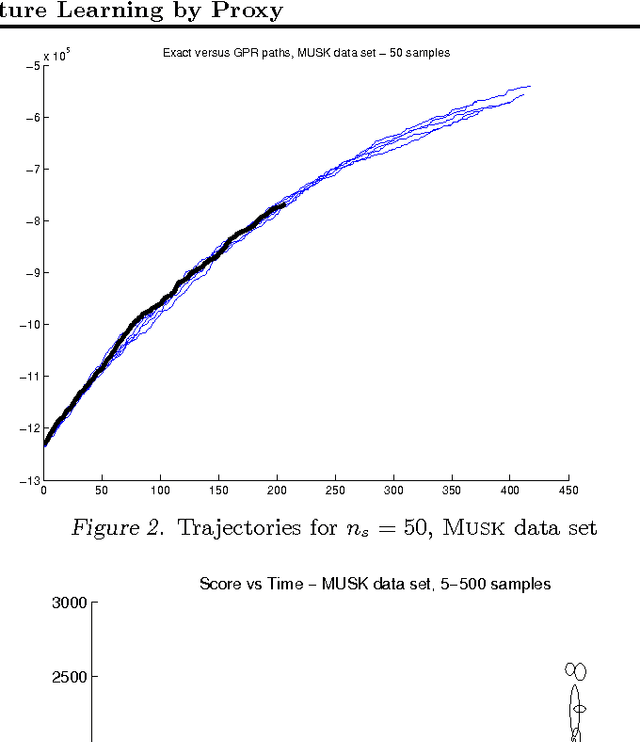
As data sets grow in size, the ability of learning methods to find structure in them is increasingly hampered by the time needed to search the large spaces of possibilities and generate a score for each that takes all of the observed data into account. For instance, Bayesian networks, the model chosen in this paper, have a super-exponentially large search space for a fixed number of variables. One possible method to alleviate this problem is to use a proxy, such as a Gaussian Process regressor, in place of the true scoring function, training it on a selection of sampled networks. We prove here that the use of such a proxy is well-founded, as we can bound the smoothness of a commonly-used scoring function for Bayesian network structure learning. We show here that, compared to an identical search strategy using the network?s exact scores, our proxy-based search is able to get equivalent or better scores on a number of data sets in a fraction of the time.

Active Learning for Node Classification in Assortative and Disassortative Networks

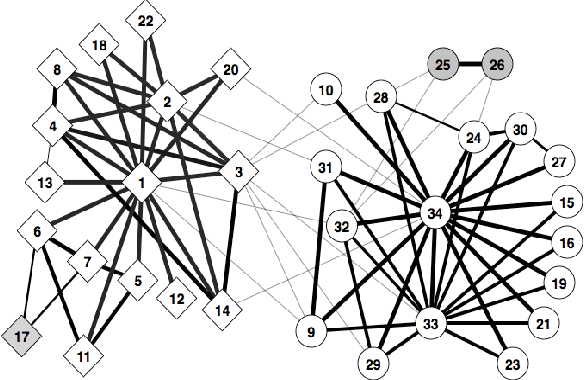
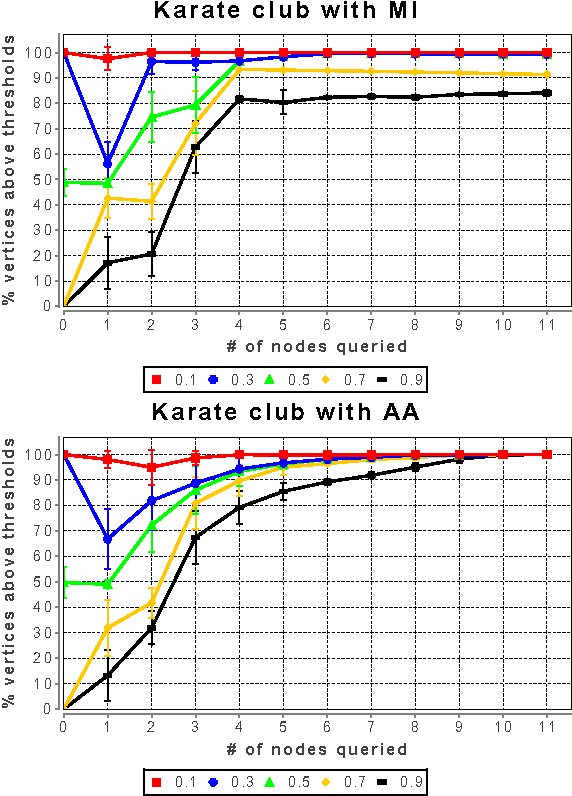
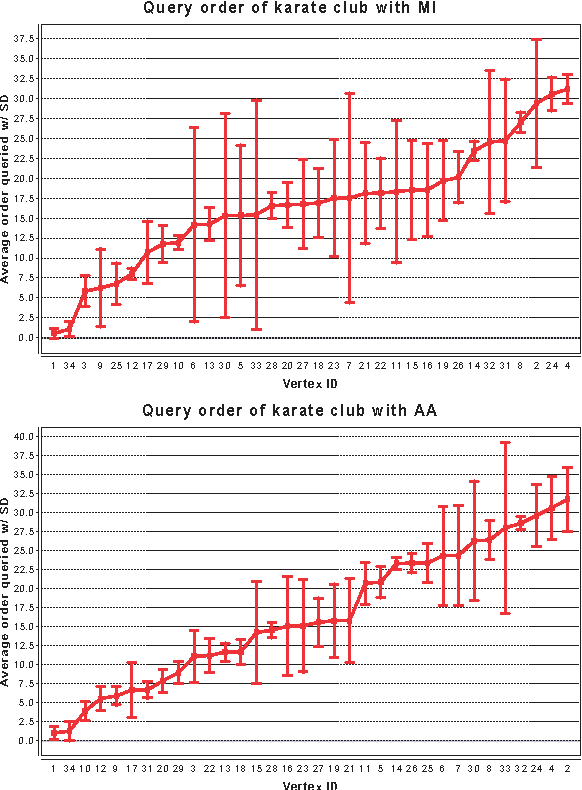
In many real-world networks, nodes have class labels, attributes, or variables that affect the network's topology. If the topology of the network is known but the labels of the nodes are hidden, we would like to select a small subset of nodes such that, if we knew their labels, we could accurately predict the labels of all the other nodes. We develop an active learning algorithm for this problem which uses information-theoretic techniques to choose which nodes to explore. We test our algorithm on networks from three different domains: a social network, a network of English words that appear adjacently in a novel, and a marine food web. Our algorithm makes no initial assumptions about how the groups connect, and performs well even when faced with quite general types of network structure. In particular, we do not assume that nodes of the same class are more likely to be connected to each other---only that they connect to the rest of the network in similar ways.

Directional Statistics on Permutations

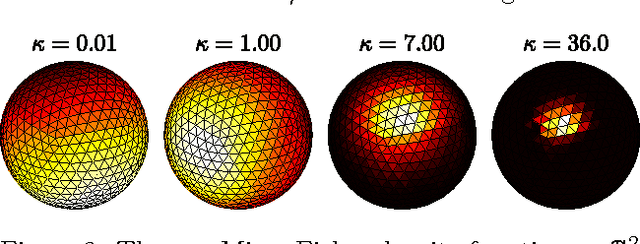
Distributions over permutations arise in applications ranging from multi-object tracking to ranking of instances. The difficulty of dealing with these distributions is caused by the size of their domain, which is factorial in the number of considered entities ($n!$). It makes the direct definition of a multinomial distribution over permutation space impractical for all but a very small $n$. In this work we propose an embedding of all $n!$ permutations for a given $n$ in a surface of a hypersphere defined in $\mathbbm{R}^{(n-1)^2}$. As a result of the embedding, we acquire ability to define continuous distributions over a hypersphere with all the benefits of directional statistics. We provide polynomial time projections between the continuous hypersphere representation and the $n!$-element permutation space. The framework provides a way to use continuous directional probability densities and the methods developed thereof for establishing densities over permutations. As a demonstration of the benefits of the framework we derive an inference procedure for a state-space model over permutations. We demonstrate the approach with applications.

Multiplicative updates For Non-Negative Kernel SVM

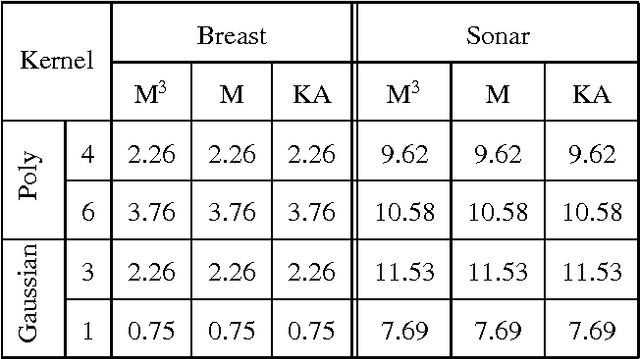
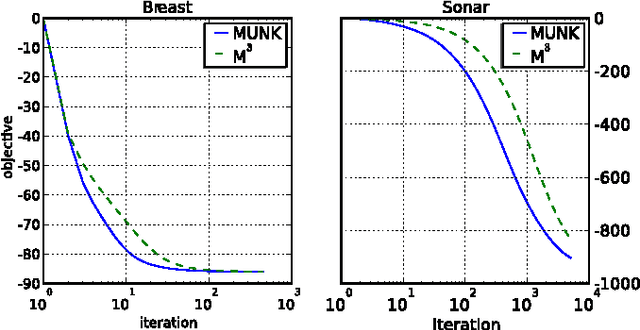
We present multiplicative updates for solving hard and soft margin support vector machines (SVM) with non-negative kernels. They follow as a natural extension of the updates for non-negative matrix factorization. No additional param- eter setting, such as choosing learning, rate is required. Ex- periments demonstrate rapid convergence to good classifiers. We analyze the rates of asymptotic convergence of the up- dates and establish tight bounds. We test the performance on several datasets using various non-negative kernels and report equivalent generalization errors to that of a standard SVM.

The Impact of Social Networks on Multi-Agent Recommender Systems

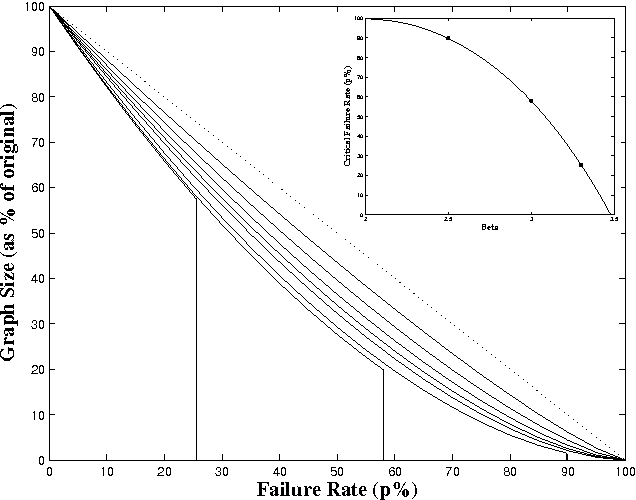
Awerbuch et al.'s approach to distributed recommender systems (DRSs) is to have agents sample products at random while randomly querying one another for the best item they have found; we improve upon this by adding a communication network. Agents can only communicate with their immediate neighbors in the network, but neighboring agents may or may not represent users with common interests. We define two network structures: in the ``mailing-list model,'' agents representing similar users form cliques, while in the ``word-of-mouth model'' the agents are distributed randomly in a scale-free network (SFN). In both models, agents tell their neighbors about satisfactory products as they are found. In the word-of-mouth model, knowledge of items propagates only through interested agents, and the SFN parameters affect the system's performance. We include a summary of our new results on the character and parameters of random subgraphs of SFNs, in particular SFNs with power-law degree distributions down to minimum degree 1. These networks are not as resilient as Cohen et al. originally suggested. In the case of the widely-cited ``Internet resilience'' result, high failure rates actually lead to the orphaning of half of the surviving nodes after 60% of the network has failed and the complete disintegration of the network at 90%. We show that given an appropriate network, the communication network reduces the number of sampled items, the number of messages sent, and the amount of ``spam.'' We conclude that in many cases DRSs will be useful for sharing information in a multi-agent learning system.