Directional Statistics on Permutations
Paper and Code
Jul 14, 2010
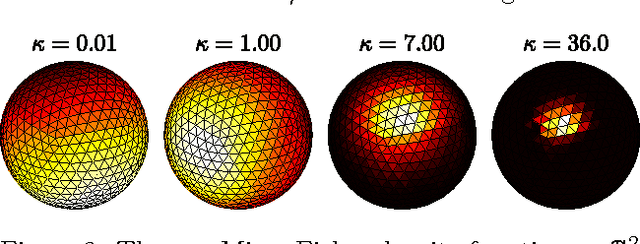

Distributions over permutations arise in applications ranging from multi-object tracking to ranking of instances. The difficulty of dealing with these distributions is caused by the size of their domain, which is factorial in the number of considered entities ($n!$). It makes the direct definition of a multinomial distribution over permutation space impractical for all but a very small $n$. In this work we propose an embedding of all $n!$ permutations for a given $n$ in a surface of a hypersphere defined in $\mathbbm{R}^{(n-1)^2}$. As a result of the embedding, we acquire ability to define continuous distributions over a hypersphere with all the benefits of directional statistics. We provide polynomial time projections between the continuous hypersphere representation and the $n!$-element permutation space. The framework provides a way to use continuous directional probability densities and the methods developed thereof for establishing densities over permutations. As a demonstration of the benefits of the framework we derive an inference procedure for a state-space model over permutations. We demonstrate the approach with applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge