Active Learning for Node Classification in Assortative and Disassortative Networks

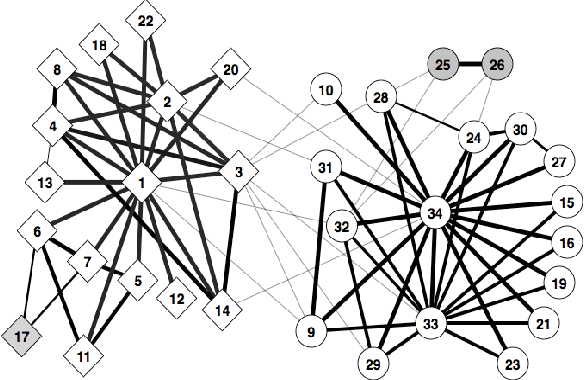
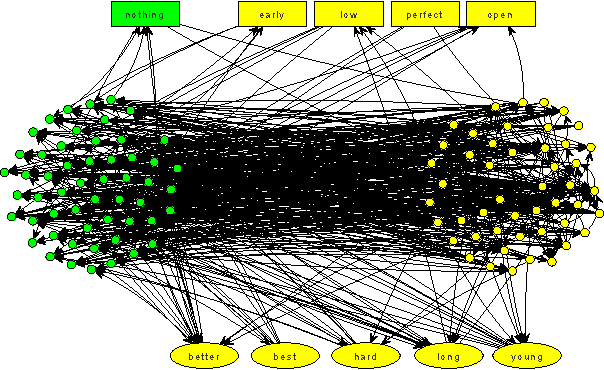
In many real-world networks, nodes have class labels, attributes, or variables that affect the network's topology. If the topology of the network is known but the labels of the nodes are hidden, we would like to select a small subset of nodes such that, if we knew their labels, we could accurately predict the labels of all the other nodes. We develop an active learning algorithm for this problem which uses information-theoretic techniques to choose which nodes to explore. We test our algorithm on networks from three different domains: a social network, a network of English words that appear adjacently in a novel, and a marine food web. Our algorithm makes no initial assumptions about how the groups connect, and performs well even when faced with quite general types of network structure. In particular, we do not assume that nodes of the same class are more likely to be connected to each other---only that they connect to the rest of the network in similar ways.

Active Learning for Hidden Attributes in Networks

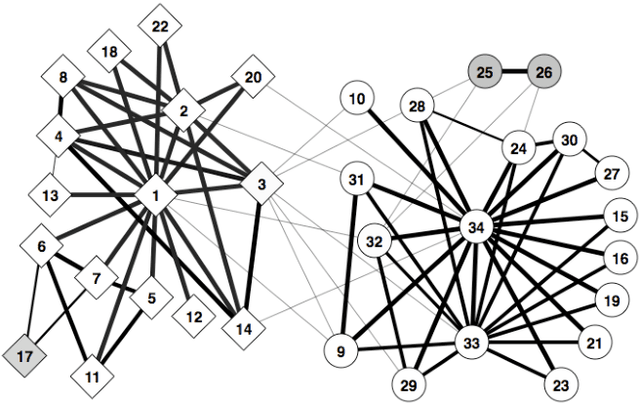
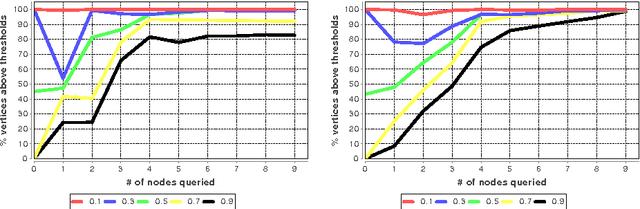
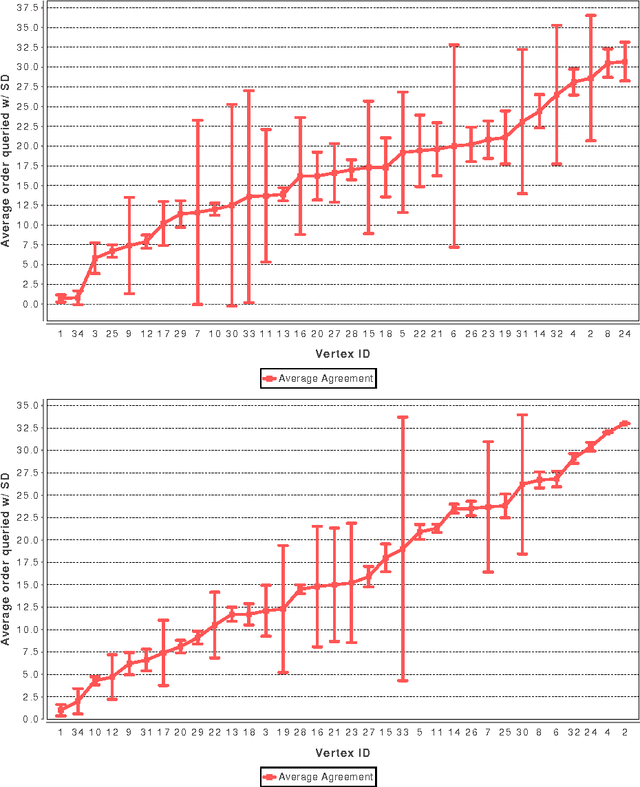
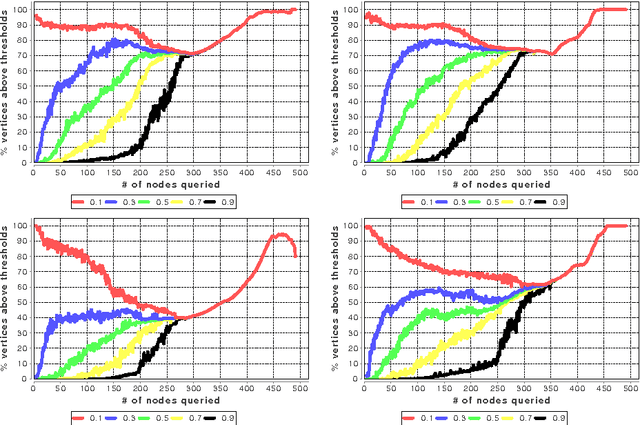
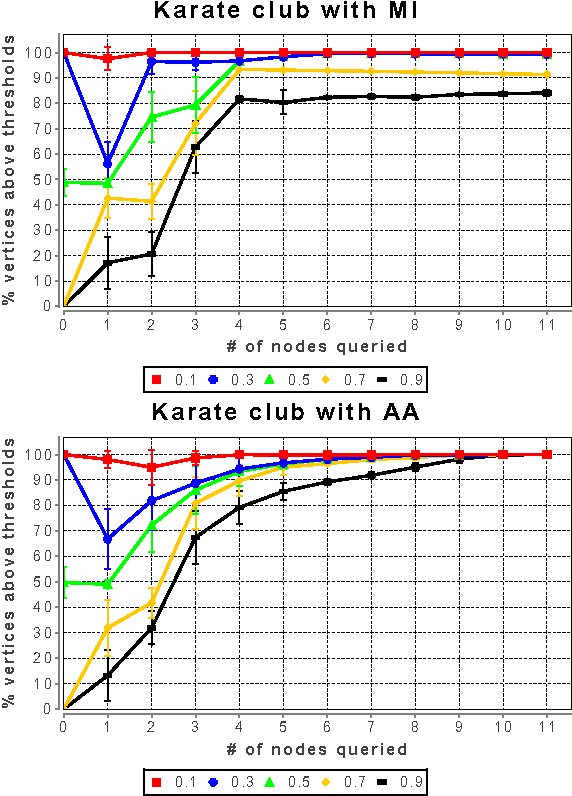
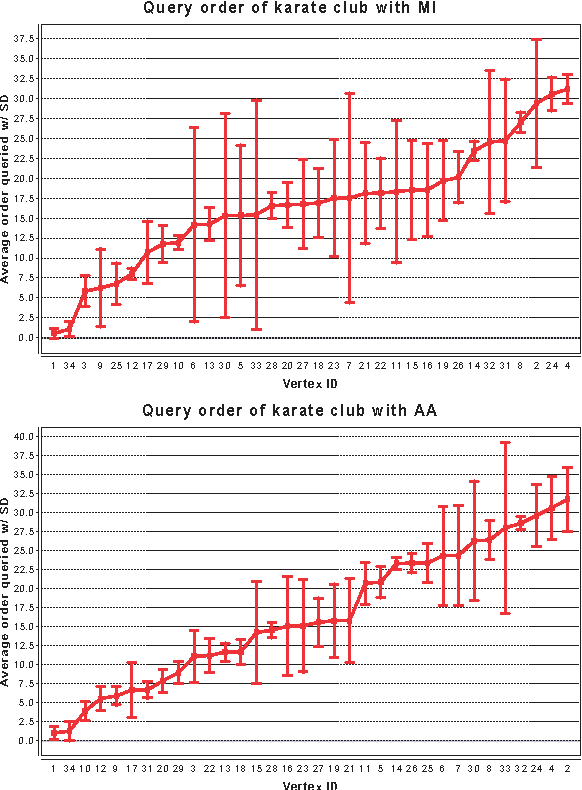
In many networks, vertices have hidden attributes, or types, that are correlated with the networks topology. If the topology is known but these attributes are not, and if learning the attributes is costly, we need a method for choosing which vertex to query in order to learn as much as possible about the attributes of the other vertices. We assume the network is generated by a stochastic block model, but we make no assumptions about its assortativity or disassortativity. We choose which vertex to query using two methods: 1) maximizing the mutual information between its attributes and those of the others (a well-known approach in active learning) and 2) maximizing the average agreement between two independent samples of the conditional Gibbs distribution. Experimental results show that both these methods do much better than simple heuristics. They also consistently identify certain vertices as important by querying them early on.